2022-09-21：有n个动物重量分别是a1、a2、a3.....an， 这群动物一起玩叠罗汉游戏， 规定从左往右

2022-09-21：有n个动物重量分别是a1、a2、a3.....an， 这群动物一起玩叠罗汉游戏， 规定从左往右选择动物，每只动物左边动物的总重量不能超过自己的重量 返回最多能选多少个动物，求一个高效的算法。 比如有7个动物，从左往右重量依次为：1，3，5，7，9，11，21 则最多能选5个动物：1，3，5，9，21 注意本题给的例子是有序的，但是实际给定的动物数组，可能是无序的， 要求从左往右选动物，且不能打乱原始数组。

答案2022-09-21：

联想到最长递增子序列。动态规划+二分。 时间复杂度O(N*logN)。 额外空间复杂度O(N)。

代码用rust编写。代码如下：

use rand::Rng;
fn main() {
    let nn = 100;
    let vv = 1000;
    let test_time = 2000;
    println!("测试开始");
    for _ in 0..test_time {
        let n = rand::thread_rng().gen_range(0, nn) + 1;
        let mut arr = random_array(n, vv);
        let ans1 = max_animals1(&mut arr);
        let ans2 = max_animals2(&mut arr);
        if ans1 != ans2 {
            println!("出错了");
            println!("{:?}", arr);
            println!("");
            println!("ans1 = {}", ans1);
            println!("ans2 = {}", ans2);
            break;
        }
    }
    println!("测试结束");
}

// 普通动态规划
// 非常一般的方法
// 来自背包的思路
fn max_animals1(arr: &mut Vec<i32>) -> i32 {
    let mut sum = 0;
    for num in arr.iter() {
        sum += *num;
    }
    let mut dp: Vec<Vec<i32>> = vec![];
    for i in 0..arr.len() as i32 {
        dp.push(vec![]);
        for _ in 0..sum + 1 {
            dp[i as usize].push(0);
        }
    }
    for i in 0..arr.len() as i32 {
        for j in 0..=sum {
            dp[i as usize][j as usize] = -1;
        }
    }
    return process1(arr, 0, 0, &mut dp);
}

fn process1(arr: &mut Vec<i32>, index: i32, pre: i32, dp: &mut Vec<Vec<i32>>) -> i32 {
    if index == arr.len() as i32 {
        return 0;
    }
    if dp[index as usize][pre as usize] != -1 {
        return dp[index as usize][pre as usize];
    }
    let p1 = process1(arr, index + 1, pre, dp);
    let mut p2 = 0;
    if arr[index as usize] >= pre {
        p2 = 1 + process1(arr, index + 1, pre + arr[index as usize], dp);
    }
    let ans = get_max(p1, p2);
    dp[index as usize][pre as usize] = ans;
    return ans;
}

// 最优解
// 如果arr长度为N，时间复杂度O(N*logN)
fn max_animals2(arr: &mut Vec<i32>) -> i32 {
    if arr.len() == 0 {
        return 0;
    }
    // ends数组
    let mut ends: Vec<i32> = vec![];
    for _ in 0..arr.len() + 1 {
        ends.push(0);
    }
    ends[0] = 0;
    let mut ends_size = 1;
    let mut max: i32 = 1;
    for i in 0..arr.len() as i32 {
        let mut l: i32 = 0;
        let mut r: i32 = ends_size - 1;
        let mut m: i32;
        let mut find: i32 = 0;
        while l <= r {
            m = (l + r) / 2;
            if ends[m as usize] <= arr[i as usize] {
                find = m;
                l = m + 1;
            } else {
                r = m - 1;
            }
        }
        if find == ends_size - 1 {
            ends[ends_size as usize] = ends[(ends_size - 1) as usize] + arr[i as usize];
            ends_size += 1;
        } else {
            if ends[(find + 1) as usize] > ends[find as usize] + arr[i as usize] {
                ends[(find + 1) as usize] = ends[find as usize] + arr[i as usize];
            }
        }
        max = get_max(max, find + 1);
    }
    return max;
}

fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a > b {
        a
    } else {
        b
    }
}

// 为了测试
fn random_array(n: i32, v: i32) -> Vec<i32> {
    let mut arr: Vec<i32> = vec![];
    for _ in 0..n {
        arr.push(rand::thread_rng().gen_range(0, v) + 1);
    }
    return arr;
}

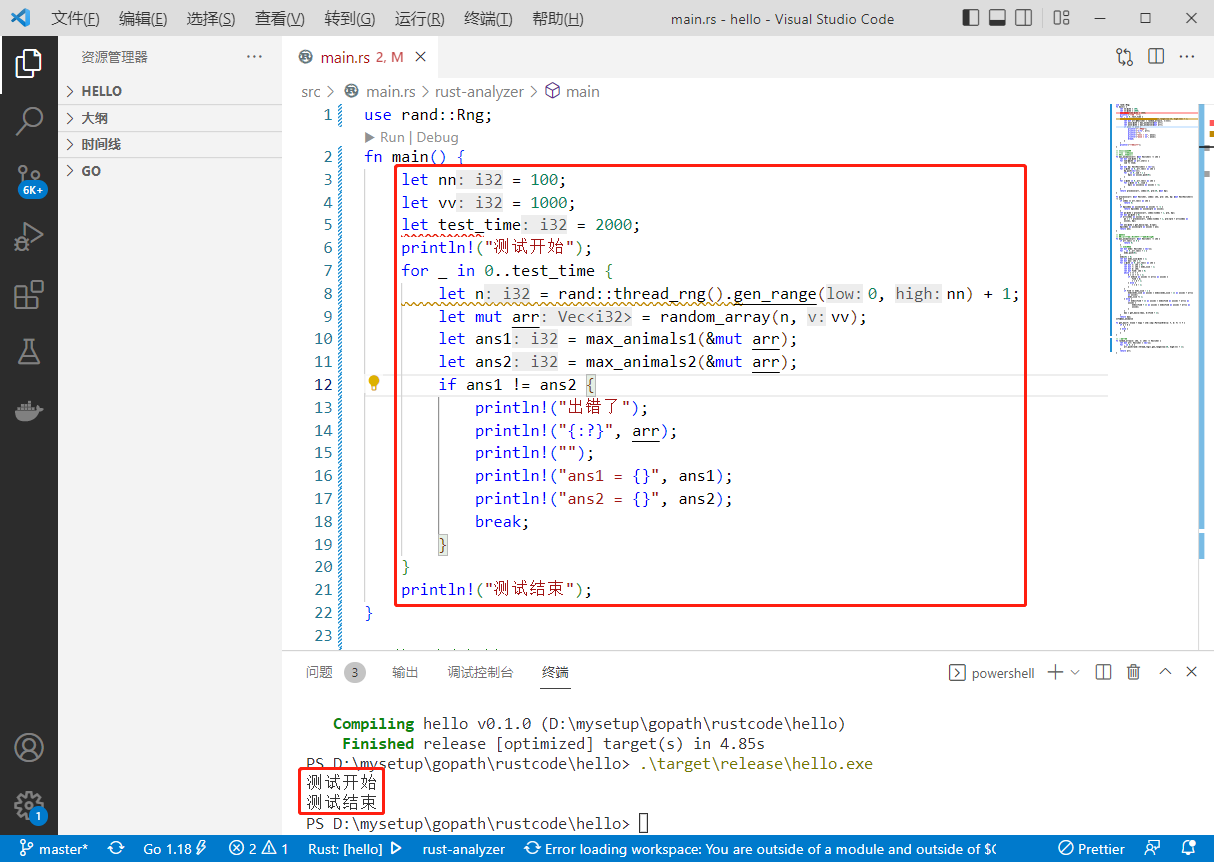
执行结果如下：

左神java代码