Count a * bTime Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 1571 Accepted Submission(s): 523 Problem Description Marry likes to count the number of ways to choose two non-negative integers a and b less than m to make a×b mod m≠0 .Let's denote f(m) as the number of ways to choose two non-negative integers a and b less than m to make a×b mod m≠0 . She has calculated a lot of f(m) for different m , and now she is interested in another function g(n)=∑m|nf(m) . For example, g(6)=f(1)+f(2)+f(3)+f(6)=0+1+4+21=26 . She needs you to double check the answer.
Give you n . Your task is to find g(n) modulo 264 .
Input The first line contains an integer T indicating the total number of test cases. Each test case is a line with a positive integer n .
Output For each test case, print one integer s , representing g(n) modulo 264 .
Sample Input
2 6 514
Sample Output
26 328194
这道题就是求
推到这一步,然后就有了一种sqrt(n)的解法 然而T=20000 于是成功卡常 参考唯一分解定理
于是现在可以先筛一个素数表 复杂度sqrt(n)以内的质数 sqrt(n)/ln(n) 比上一种方法快几倍 这道题时间卡得很紧
然而,成功爆unsigned long long
在这里, 引入__int128成功卡过
网上还有其他的防止溢出的方法
|




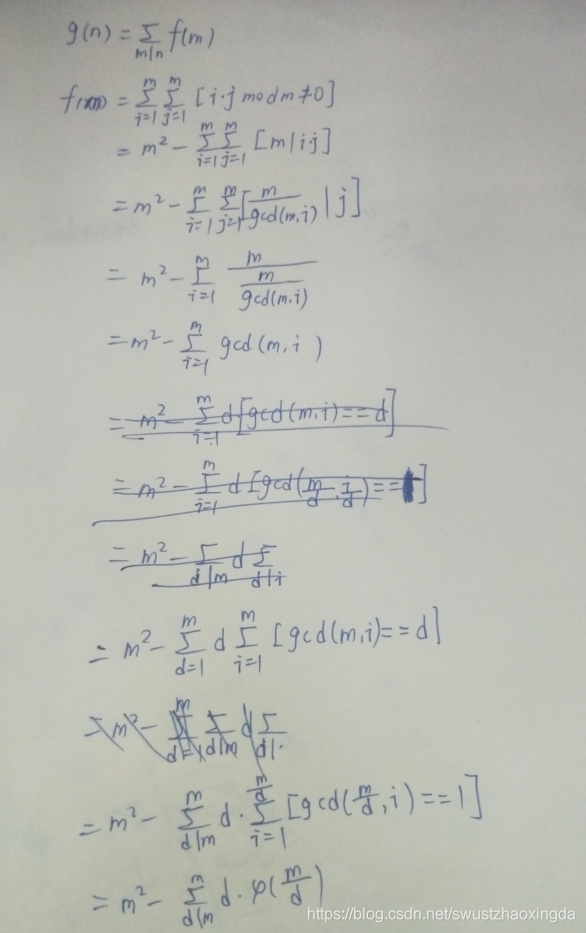



 京公网安备 11010502036488号
京公网安备 11010502036488号