2022-07-15：一开始有21个球，甲和乙轮流拿球，甲先、乙后， 每个人在自己的回合，一定要拿不超过3个球，不能不拿。 最终谁的总球数为偶数，谁赢。 请问谁有必胜策略。 来自微众。人工智能岗。

答案2022-07-15：

21球，是甲赢。如果把21变成其他正整数，误以为甲也一定赢，但实际上是不一定。可能甲赢，乙赢，打平。 通过递归可以发现规律。1甲 3乙 5乙 7乙，9甲 11乙 13乙 15乙。

代码用rust编写。代码如下：

fn main() {
    let mut i = 1;
    while i < 500 {
        //let ans = win1(i,0,0,0);
        let ans = win(i);
        println!("i = {},ans = {}", i, ans);
        i += 2;
    }
}

// balls = 21
// ball是奇数
fn win(balls: i32) -> String {
    return process(0, balls, 0, 0);
}
// 憋递归！
// turn 谁的回合！
// turn == 0 甲回合
// turn == 1 乙回合
// rest剩余球的数量
// 之前，jiaBalls、yiBalls告诉你！
// 当前，根据turn，知道是谁的回合！
// 当前，还剩多少球，rest
// 返回：谁会赢！
fn process(turn: i32, rest: i32, jia: i32, yi: i32) -> String {
    if rest == 0 {
        return if (jia & 1) == 0 {
            String::from("甲")
        } else {
            String::from("乙")
        };
    }
    // rest > 0, 还剩下球！
    if turn == 0 {
        // 甲的回合！
        // 甲，自己赢！甲赢！
        for pick in 1..=get_min(rest, 3) {
            // pick 甲当前做的选择
            if process(1, rest - pick, jia + pick, yi) == "甲" {
                return String::from("甲");
            }
        }
        return String::from("乙");
    } else {
        for pick in 1..=get_min(rest, 3) {
            // pick 甲当前做的选择
            if process(0, rest - pick, jia, yi + pick) == ("乙") {
                return String::from("乙");
            }
        }
        return String::from("甲");
    }
}

fn get_min<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a < b {
        a
    } else {
        b
    }
}

// 我们补充一下设定，假设一开始的球数量不是21，是任意的正数
// 如果最终两个人拿的都是偶数，认为无人获胜，平局
// 如果最终两个人拿的都是奇数，认为无人获胜，平局
// rest代表目前剩下多少球
// cur == 0 代表目前是甲行动
// cur == 1 代表目前是乙行动
// first == 0 代表目前甲所选的球数，加起来是偶数
// first == 1 代表目前甲所选的球数，加起来是奇数
// second == 0 代表目前乙所选的球数，加起来是偶数
// second == 1 代表目前乙所选的球数，加起来是奇数
// 返回选完了rest个球，谁会赢，只会返回"甲"、"乙"、"平"
// win1方法，就是彻底暴力的做所有尝试，并且返回最终的胜利者
// 在甲的回合，甲会尝试所有的可能，以保证自己会赢，如果自己怎么都不会赢，那也要尽量平局，如果这个也不行，只能对方赢
// 在乙的回合，乙会尝试所有的可能，以保证自己会赢，如果自己怎么都不会赢，那也要尽量平局，如果这个也不行，只能对方赢
// 算法和数据结构体系学习班，视频39章节，牛羊吃草问题，就是类似这种递归
fn win1(rest: i32, cur: i32, first: i32, second: i32) -> String {
    if rest == 0 {
        if first == 0 && second == 1 {
            return String::from("甲");
        }
        if first == 1 && second == 0 {
            return String::from("乙");
        }
        return String::from("平");
    }
    if cur == 0 {
        // 甲行动
        let mut best_ans = String::from("乙");
        for pick in 1..=get_min(3, rest) {
            let mut cur_ans = win1(rest - pick, 1, first ^ (pick & 1), second);
            if cur_ans == "甲" {
                best_ans = String::from("甲");
                break;
            }
            if cur_ans == "平" {
                best_ans = String::from("平");
            }
        }
        return best_ans;
    } else {
        // 乙行动
        let mut best_ans = String::from("甲");
        for pick in 1..=get_min(3, rest) {
            let mut cur_ans = win1(rest - pick, 0, first, second ^ (pick & 1));
            if cur_ans == "乙" {
                best_ans = String::from("乙");
                break;
            }
            if cur_ans == "平" {
                best_ans = String::from("平");
            }
        }
        return best_ans;
    }
}

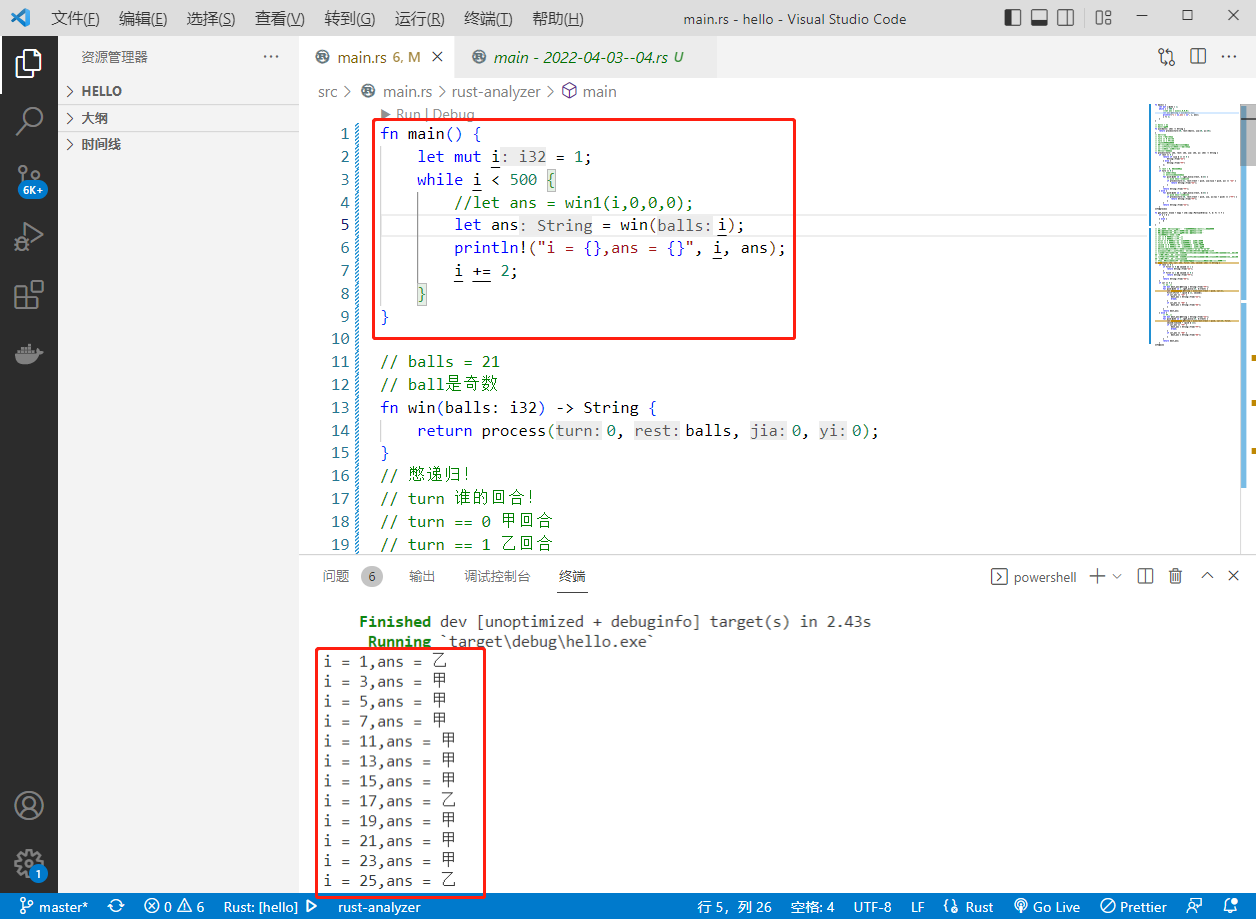
执行结果如下：

在这里插入图片描述

左神java代码