D. Half Turns
Solution
看不懂题解写的什么……
n和m都为偶数,是一定可以构造出解的。
我们假设,然后分类:
当时,按照如下方式构造

即第一列和最后一列都是拐弯点,中间可以放2的倍数个拐弯点。
接下来考虑n=6的时候,按照如下方式构造
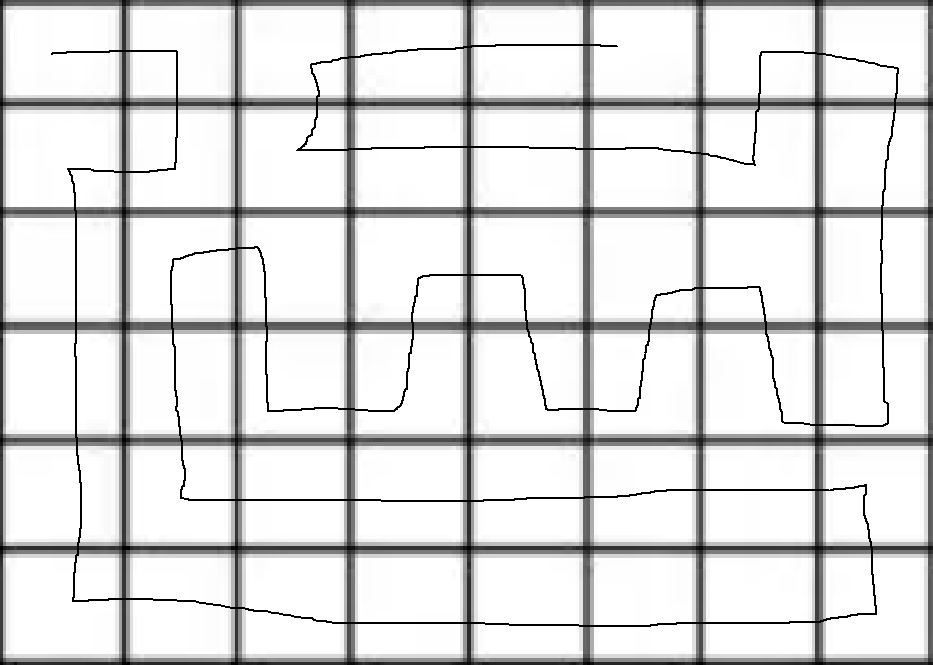
第一、二行从第三列开始的部分可以放2的倍数个拐弯点。
然后考虑n比较大的时候,我们可以将每四行看成一个整体来做,如果n不是4的倍数那么最后一块就包含6行。
先考虑中间的块,不考虑头尾,我们希望能在这4行内构造2m个拐弯点,用如下方式构造
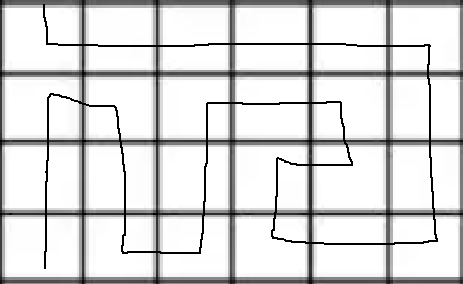
这样就能保证中间每一块从第一列进入,又从第一列出去。
接下来考虑头尾,当n是4的倍数的时候只需要放一个头部就行了,如下

当n不是4的倍数时,最后一块可以构造成3m+1个拐弯点,第一块可以构造成2m-1个拐弯点,第一块构造如下

最后一块构造如下
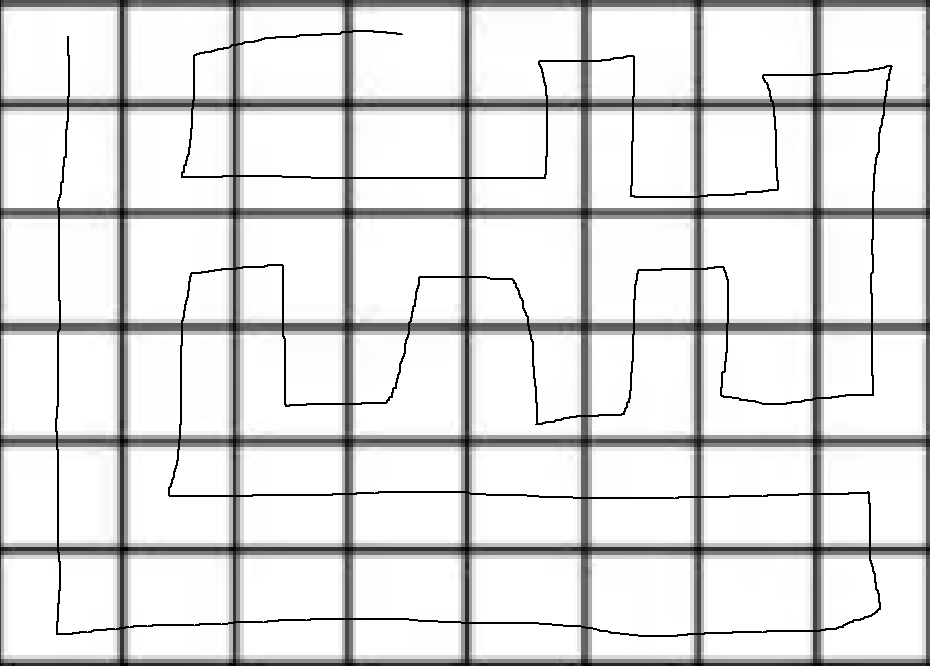
时间复杂度。
int ans[N][N];
int main() {
int n = fast_IO::read(), m = fast_IO::read(), tag = 0;
if (n > m)swap(n, m), tag = 1;
if (n == 2) {
int x, y, num;
x = 2, y = 3, num = 6;
ans[1][2] = 1, ans[1][1] = 2, ans[2][1] = 3, ans[2][2] = 4;
ans[2][3] = 5;
for (int i = 1, now = 0; i <= m - 4; ++i) {
if (!now) {
x = 3 - x;
now = 1;
}
else ++y, now = 0;
ans[x][y] = num++;
}
while (y < m) {
++y;
ans[x][y] = num++;
}
x = 3 - x;
while (num <= n * m) {
ans[x][y] = num++;
--y;
}
}
else if (n == 6) {
int x = 1, y = 1, num = 1;
ans[x][y] = num++;
++y;
ans[x][y] = num++;
++x;
ans[x][y] = num++;
--y;
ans[x][y] = num++;
while (x < n) {
++x;
ans[x][y] = num++;
}
while (y < m) {
++y;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
while (y > 2) {
--y;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
for (int i = 1, now = 0; i < 2 * (m - 1); ++i) {
if (!now)x = n - 4 + 3 - (x - (n - 4)), now = 1;
else ++y, now = 0;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
for (int i = 1, now = 0; i <= m - 5; ++i) {
if (!now)x = n - 6 + 3 - (x - (n - 6)), now = 1;
else --y, now = 0;
ans[x][y] = num++;
}
while (y > 3) {
--y;
ans[x][y] = num++;
}
x = n - 6 + 3 - (x - (n - 6));
while (num <= n * m) {
ans[x][y] = num++;
++y;
}
}
else {
int x = 0, y = 1, num = 1;
if (n % 4 == 0) {
ans[4][m] = 1;
x = 4, y = m, num = 2;
}
else {
x = 3, y = m - 1;
ans[x][y] = num++;
++y;
ans[x][y] = num++;
++x;
ans[x][y] = num++;
--y;
ans[x][y] = num++;
--y;
ans[x][y] = num++;
}
for (int i = 1, now = 0; x != 3 || y != 2; ++i) {
if (!now) {
x = 2 + 3 - (x - 2);
now = 1;
}
else --y, now = 0;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
while (y < m) {
++y;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
while (y > 1) {
--y;
ans[x][y] = num++;
}
while (x < 4) {
++x;
ans[x][y] = num++;
}
for (int i = 5; (n % 4 == 0 ? i + 3 : i + 6) <= n; i += 4) {
++x;
ans[x][y] = num++;
while (y < m) {
++y;
ans[x][y] = num++;
}
while (x < i + 3) {
++x;
ans[x][y] = num++;
}
--y;
ans[x][y] = num++;
--y;
ans[x][y] = num++;
--x;
ans[x][y] = num++;
++y;
ans[x][y] = num++;
--x;
ans[x][y] = num++;
--y;
ans[x][y] = num++;
for (int j = 1, now = 0; j <= 2 * (m - 3); ++j) {
if (!now) {
--y;
now = 1;
}
else {
if (x == i + 3) {
--x;
ans[x][y] = num++;
--x;
}
else {
++x;
ans[x][y] = num++;
++x;
}
now = 0;
}
ans[x][y] = num++;
}
}
if (n % 4 == 2) {
while (x < n) {
++x;
ans[x][y] = num++;
}
while (y < m) {
++y;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
while (y > 2) {
--y;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
for (int i = 1, now = 0; i < 2 * (m - 1); ++i) {
if (!now)x = n - 4 + 3 - (x - (n - 4)), now = 1;
else ++y, now = 0;
ans[x][y] = num++;
}
--x;
ans[x][y] = num++;
for (int i = 1, now = 0; i < m; ++i) {
if (!now)x = n - 6 + 3 - (x - (n - 6)), now = 1;
else --y, now = 0;
ans[x][y] = num++;
}
while (y > 2) {
--y;
ans[x][y] = num++;
}
x = n - 6 + 3 - (x - (n - 6));
while (num <= n * m) {
ans[x][y] = num++;
++y;
}
}
}
puts("Yes");
if (tag) {
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= n; ++j)
printf("%d%c", ans[j][i], j == n ? '\n' : ' ');
}
else {
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
printf("%d%c", ans[i][j], j == m ? '\n' : ' ');
}
return 0;
}




 京公网安备 11010502036488号
京公网安备 11010502036488号