题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1392

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him?
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.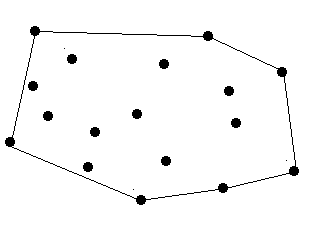



There are no more than 100 trees.

 

 

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.

Zero at line for number of trees terminates the input for your program.

 

 

Output

The minimal length of the rope. The precision should be 10^-2.

 

 

Sample Input


 

9 12 7 24 9 30 5 41 9 80 7 50 87 22 9 45 1 50 7 0

 

 

Sample Output


 

243.06

 

题目大意：随即给出n个点，求出一个最小的多边形把这n个点都包进去（点可以在线上）

输入点，极角排序，对于每个点，若在左边，放弃上一个点，若在右边，更新入边集

ac：

#include<stdio.h>
#include<string.h>  
#include<math.h>  
  
//#include<map>   
//#include<set>
#include<deque>  
#include<queue>  
#include<stack>  
#include<bitset> 
#include<string>  
#include<iostream>  
#include<algorithm>  
using namespace std;  

#define ll long long  
#define INF 0x3f3f3f3f  
#define mod 1000000007
//#define max(a,b) (a)>(b)?(a):(b)
//#define min(a,b) (a)<(b)?(a):(b) 
#define clean(a,b) memset(a,b,sizeof(a))// 水印 
//std::ios::sync_with_stdio(false);
struct node{
	double x,y;
//	node& operator - (node &a){
//		x=x-a.x;
//		y=y-a.y;
//		return *this;
//	}
    node friend operator - (node a,node b) {
        return {a.x - b.x, a.y - b.y};
    }
	node (double _x=0,double _y=0):x(_x),y(_y){}
}dot[110],st[110];

double cross(node a,node b)
{
	return a.x*b.y-a.y*b.x;
}

double seek_l(node a,node b)
{
	node c=a-b;
	return sqrt(c.x*c.x+c.y*c.y);
}

bool cmp(node a,node b)
{
	double x=cross(a-dot[1],b-dot[1]);
	if(x>0)
		return 1;
	if(x==0&&seek_l(a,dot[1])<seek_l(b,dot[1]))
		return 1;
	return 0;
}

int main()
{
	std::ios::sync_with_stdio(false);
	int n;
	while(cin>>n&&n)
	{
		for(int i=1;i<=n;++i)
			cin>>dot[i].x>>dot[i].y;
		if(n==1)
		{
			cout<<"0.00"<<endl;
			continue;
		}
		else if(n==2)
		{
			printf("%.2lf\n",seek_l(dot[1],dot[2]));
			continue;
		}
		int k=1;
		for(int i=2;i<=n;++i)
		{
			if(dot[i].y<dot[k].y||(dot[i].y==dot[k].y&&dot[i].x<dot[k].x))
				k=i;
		}
		swap(dot[1],dot[k]);
		sort(dot+2,dot+n+1,cmp);//极角排序
		st[1]=dot[1];
		st[2]=dot[2];
		int tot=2;
		for(int i=3;i<=n;++i)
		{
			while(tot>=2&&cross(st[tot]-st[tot-1],dot[i]-st[tot-1])<=0)
				tot--;
			st[++tot]=dot[i];
		}
		st[tot+1]=st[1];
		double ans=0;
		for(int i=1;i<=tot;++i)
			ans=ans+seek_l(st[i],st[i+1]);
		printf("%.2lf\n",ans);
	}
}