验题人题解

更好的阅读体验：见我的博客

前言

这套卷子我没参与命题，是由我校「CF橙名学弟 周」一个人造的题目，比我造的那套第 9 届的卷子「友好很多」也没有（赞~）

偶数届是团队赛

原先，我想加一道博弈论，缓一下AK速度的。

但商量后，还是没加。 因为校内肯定没人会做，有点浪费。

我验完了所有题，出题人的所有锅都被我踩出来了(bushi)，所以大伙做起来应该挺顺的（QAQ）

顺便来写一个简略版的题解吧~~

A、 活动

设 表示前 个人分组的方案

考虑从第 个人所在的组，是几人组，从前面第 个人选出一些人跟他组队：

• ，二人组，剩下的人组队方案为
• ，三人组，剩下的人组队方案为
• ，四人组，剩下的人组队方案为

可以理解为，选出来的 个人跟他组队，其他人重新编号为 ，他们的组队方案就是 ​

预处理，然后直接输出答案即可。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 7e6 + 10, md = 998244353;
constexpr int INF = 0x3f3f3f3f;

int n, m;

LL fpow(LL a, LL b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1)
            res = res * a % md;
        a = a * a % md;
        b >>= 1;
    }
    return res;
}
LL fac[N], ifac[N];
void initFac(int n)
{
    fac[0] = 1;
    for(int i = 1; i <= n; i ++)
        fac[i] = fac[i - 1] * i % md;
    ifac[n] = fpow(fac[n], md - 2);
    for(int i = n; i >= 1; i --)
        ifac[i - 1] = ifac[i] * i % md;
    assert(ifac[0] == 1);
}
LL C(int n, int m)
{
    if(n < 0 || m < 0 || n < m)
        return 0;
    return fac[n] * ifac[m] % md * ifac[n - m] % md;
}

LL add(LL a, LL b)
{
    return (a + b) % md;
}
LL mul(LL a, LL b)
{
    return a * b % md;
}
void addNorm(LL &a)
{
    if(a >= md)
        a -= md;
}
void norm(LL &a)
{
    a %= md;
}

LL f[N];
void init(int n)
{
    initFac(n);
    f[0] = 1;
    f[1] = 0;
    f[2] = f[3] = 1;
    rep(i, 4, n)
    {
        // 2
        f[i] = C(i - 1, 1) * f[i - 2] % md;
        f[i] += C(i - 1, 2) * f[i - 3] % md;
        norm(f[i]);
        f[i] += C(i - 1, 3) * f[i - 4] % md;
        norm(f[i]);
        if(f[i] < 0)
            f[i] += md;
    }   
}

void solve()
{
    cin >> n;
    cout << f[n] << el;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    init(N - 1);
    int T;
    cin >> T;
    while(T --)
    {
        solve();
    }
}

B、矩阵的拆解之谜

可以注意到一个性质，

• 反对称阵的对称位置之和为 。

所以一个矩阵位置合法，需要对称位置之和 是偶数。

于是对称阵的元素，我们设置为

反对称阵就设置为：原来的值跟 的差值即可。

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;

void solve()
{
    cin >> n;
    assert(n <= 500 && n >= 1);
    vector a(n + 1, vector<int>(n + 1));
    rep(i, 1, n)
    {
        rep(j, 1, n)
        {
            cin >> a[i][j];
            assert(a[i][j] >= -1e9 && a[i][j] <= 1e9);
        }
    }
    vector b(n + 1, vector<int>(n + 1));
    vector c(n + 1, vector<int>(n + 1));
    bool ok = true;
    rep(i, 1, n)
    {
        rep(j, i, n)
        {
            if (i != j)
            {
                int val = a[i][j] + a[j][i];
                if (val & 1)
                {
                    ok = false;
                    cout << "NO" << el;
                    exit(0);
                }
                else
                {
                    int x = val / 2;
                    b[i][j] = b[j][i] = x;
                    int y = a[i][j] - x;
                    c[i][j] = y;
                    c[j][i] = -y;
                }
            }
            else
            {
                // i = j
                b[i][j] = a[i][j];
            }
        }
    }
    if (ok)
    {
        cout << "YES" << el;
        rep(i, 1, n)
        {
            rep(j, 1, n)
            {
                cout << b[i][j] << " \n"[j == n];
            }
        }
        rep(i, 1, n)
        {
            rep(j, 1, n)
            {
                cout << c[i][j] << " \n"[j == n];
            }
        }
    }
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}

C、 因子数小于等于4的个数

这道题只需要知道约束的公式即可

设一个数质因数分解形式为

那么它的约数个数为

考虑每个指数部分的取值，即可得到公式

暴力约数分解即可通过这道题，时间限制很松这一题

朴素的筛法都可以通过（每个数筛它的倍数，判断一个数被筛了几次）。

#include <bits/stdc++.h>

using namespace std;

#define LL long long
#define endl '\n'

const int N = 1e6 + 1;
int f[N], pre[N];

void init()
{
    for (int i = 1; i < N; ++i)
        for (int j = i; j < N; j += i)
            f[j]++;
    for (int i = 1; i < N; ++i)
        pre[i] = pre[i - 1] + (f[i] <= 4);
}

void Solve()
{
    int T;
    cin >> T;
    assert(1 <= T && T <= 1e5);
    while (T--)
    {
        int l, r;
        cin >> l >> r;
        assert(1 <= l && l <= r && r <= 1e6);
        cout << pre[r] - pre[l - 1] << "\n";
    }
}

int main()
{
    init();
    Solve();
    return 0;
}

进一步的，也有严格 的做法，

容易发现质因数三个及以上的一定不满足，

考虑只有 个和 个的即可，记录线性筛时每个数的最小质因数 ，在筛掉的时候判断一下即可。

复杂度此时为

如下代码是 的

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;

int p[N], tot;
bool isnp[N];
int low[N];

int check(int x)
{
    unordered_map<int, int> cnt;
    while(x > 1)
    {
        cnt[low[x]] ++;
        x /= low[x];
    }
    int res = 1;
    for(auto &[k, v] : cnt)
    {
        res *= (v + 1);
    }
    return res <= 4;
}
int can[N];
int sum[N];
void init(int n)
{
    isnp[1] = true;
    can[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        if(!isnp[i])
        {
            p[ ++ tot] = i;
            low[i] = i;
            can[i] = 1;
        }
        for(int j = 1; i * p[j] <= n; j ++)
        {
            int t = i * p[j];
            isnp[t] = true;
            low[t] = p[j];

            if(i % p[j] == 0){
                if(t == 1LL * p[j] * p[j] || t == 1LL * p[j] * p[j] * p[j])
                {
                    can[t] = true;
                }
                break;
            }
            else {
                if(isnp[i] == false)
                    can[t] = true;
            }
        }
    }
    sum[1] = 1;
    rep(i, 2, n)
    {
        sum[i] = sum[i - 1] + can[i];
    }
}


void solve()
{
    
    int l, r;
    cin >> l >> r;
    assert(1 <= l && l <= r && r <= 1e6);
    int ans = sum[r] - sum[l - 1];
    cout << ans << el;
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    int T;
    init(1e6);

    cin >> T;
    assert(1 <= T && T <= 1e5);
    while(T --)
    {
        solve();
    }
}

D、 图

因为每次合并的，一定是不连通的部分，

• 故一定是一个森林。

那么我们就可以用 LCA 来快速计算树上的距离了

合并的话怎么合并？

• 对，启发式合并，小的集合合并到大的即可

于是维护倍增数组，表示节点到当前树根。

• 合并的时候，让小的树合并到大的
• 然后让这些节点，继续往上跳即可。

总时间复杂度为

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;

struct DSU
{
    std::vector<int> f, siz;
    DSU(int n) : f(n), siz(n, 1) { std::iota(f.begin(), f.end(), 0); }
    int leader(int x)
    {
        while (x != f[x])
            x = f[x] = f[f[x]];
        return x;
    }
    bool same(int x, int y) { return leader(x) == leader(y); }
    bool merge(int x, int y)
    {
        x = leader(x);
        y = leader(y);
        if (x == y)
            return false;
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }
    int size(int x) { return siz[leader(x)]; }
};
vector<int> g[N];
int fa[N], dep[N];
const int B = 20;
int f[N][B];
void dfs(int u)
{
    // 合并，往上跳
    lop(i, 1, B)
    {
        f[u][i] = f[f[u][i - 1]][i - 1];
    }
    for (auto &v : g[u])
    {
        if (v != fa[u])
        {
            dep[v] = dep[u] + 1;
            f[v][0] = fa[v] = u;
            dfs(v);
        }
    }
}

int getLca(int x, int y)
{
    // 确保开始要跳的是x
    if (dep[x] < dep[y])
        swap(x, y);
    // 跳到同一高度
    dwn(i, B - 1, 0)
    {
        if (dep[f[x][i]] >= dep[y])
            x = f[x][i];
    }
    if (x == y)
        return x;
    dwn(i, B - 1, 0)
    {
        if (f[x][i] != f[y][i])
        {
            x = f[x][i];
            y = f[y][i];
        }
    }
    return f[x][0];
}

const int P = 998244353;
void solve()
{
    int n, t;
    cin >> n >> t;
    rep(i, 0, n)
        dep[i] = 1;
    DSU dsu(n + 1);
    int last = 0;
    while (t--)
    {
        LL a, b, c;
        cin >> a >> b >> c;
        LL op = 1 + (((a * (2 + last)) % 998244353) % 2);
        LL u = 1 + (((b * (2 + last)) % 998244353) % n);
        LL v = 1 + (((c * (2 + last)) % 998244353) % n);

        if (op == 1)
        { // merge
            if (dsu.size(u) < dsu.size(v))
                swap(u, v);
            g[u].push_back(v);
            g[v].push_back(u);
            // 将v合并到u中
            dsu.merge(u, v);
            fa[v] = f[v][0] = u;
            dep[v] = dep[u] + 1;
            dfs(v); // 更新倍增数组
        }
        else
        {
            if (dsu.same(u, v))
            {
                int lca = getLca(u, v);
                auto ans = dep[u] + dep[v] - 2 * dep[lca];
                last = ans;
            }
            else {
                last = -1;
            }
            cout << last << el;
        }
    }
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}

E、琪露诺的数学题

版单可能歪了，我感觉这题还是很简单的。

也可能是大伙多项式学傻了

学的越多越不会做这题（bushi

展开交换求和顺序即可，预处理后 求解即可

因为我们只需要知道总和就可以了，不需要知道具体每个位置的值

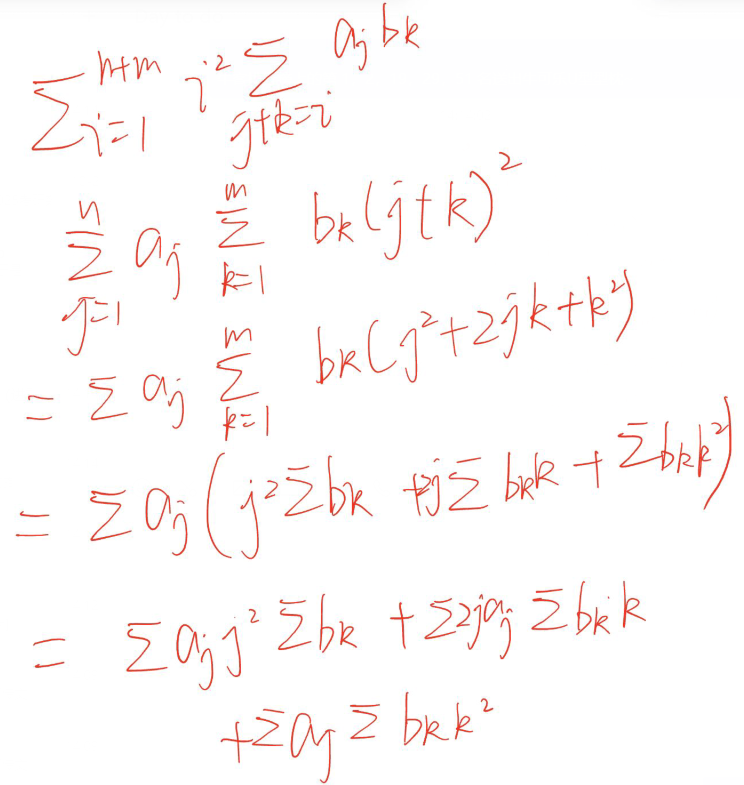
#include <bits/stdc++.h>
using namespace std;

#define int long long
#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;

LL add(LL a, LL b)
{
    
    return (a + b) % md;
}
LL mul(LL a, LL b)
{
    return a * b % md;
}
void addNorm(LL &a)
{
    if(a >= md)
        a -= md;
}
void norm(LL &a)
{
    a %= md;
}

void solve()
{
    cin >> n >> m;
    assert(1 <= n && n <= 1e6);
    assert(1 <= m && m <= 1e6);

    vector<LL> a(n + 2), b(m + 2);
    rep(i, 1, n)
    {
        cin >> a[i];
        assert(1 <= a[i] && a[i] <= 1e9);
    }
    rep(j, 1, m)
    {
        cin >> b[j];
        assert(1 <= b[j] && b[j] <= 1e9);
    }

    LL sumA = 0;
    LL sumAj = 0, sumA2 = 0;
    rep(j, 1, n)
    {
        sumA += a[j];
        sumA %= md;

        sumAj += 2 * j % md * a[j] % md;
        sumAj %= md;

        sumA2 += a[j] * j % md * j % md;
        sumA2 %= md;
    }
    LL sumB = 0;
    LL sumBk = 0, sumB2 = 0;
    rep(j, 1, m)
    {
        sumB += b[j];
        sumB %= md;

        sumBk += j * b[j] % md;
        sumBk %= md;

        sumB2 += b[j] * j % md * j % md;
        sumB2 %= md;
    }
    LL ans = 0;
    ans = mul(sumA2, sumB);
    ans = add(ans, mul(sumAj, sumBk));
    ans = add(ans, mul(sumA, sumB2));
    if(ans < 0)
        ans += md;
    cout << ans << el;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}

F、串

字符串哈希、后缀数组

首先将这个字符串在后面拷贝一份，将长度变成 ​。

然后字符串哈希，于是我们寻找子串 的第 ​ 小的字符串即可。

那么如何快速比较两个字符串的大小呢？

• 因为有哈希值这个东西，考虑最长公共前缀 LCP
• 我们去二分 LCP 的长度，每次比较哈希值，
• 然后找到第一个不同的位置，
• 直接比较大小即可

这样我们就可以在 的时间内，比较两个字符串的大小。

然后我们使用 nth_element 函数可以 时间内找到第 小的元素。

总时间复杂度为

用 sort 常数小一点应该也可以过（单哈希，pair的双哈希），这题没有卡单哈希

下面我直接用oiwiki的板子，vector常数很大，建议改掉。

另外，这题也可以用 后缀数组 过掉，

附上一张校内赛场中「我的可爱学弟」

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;

constexpr int L = 1e6 + 5;
// constexpr int HASH_CNT = 2;

// int hashBase[HASH_CNT] = {29, 31};
// int hashMod[HASH_CNT] = {int(1e9 + 9), 998244353};

constexpr int HASH_CNT = 1;

int hashBase[2] = {29, 31};
int hashMod[2] = {int(1e9 + 9), 998244353};

// 1-index
struct StringWithHash
{
    char s[L];
    int ls;
    int hsh[HASH_CNT][L];
    int pwMod[HASH_CNT][L];

    void init()
    { // 初始化
        ls = 0;
        for (int i = 0; i < HASH_CNT; ++i)
        {
            hsh[i][0] = 0;
            pwMod[i][0] = 1;
        }
    }

    StringWithHash() { init(); }

    void extend(char c)
    {
        s[++ls] = c; // 记录字符数和每一个字符
        for (int i = 0; i < HASH_CNT; ++i)
        { // 双哈希的预处理
            pwMod[i][ls] =
                1ll * pwMod[i][ls - 1] * hashBase[i] % hashMod[i]; // 得到b^ls
            hsh[i][ls] = (1ll * hsh[i][ls - 1] * hashBase[i] + c) % hashMod[i];
        }
    }

    vector<int> getHash(int l, int r)
    { // 得到哈希值
        vector<int> res(HASH_CNT, 0);
        for (int i = 0; i < HASH_CNT; ++i)
        {
            int t =
                (hsh[i][r] - 1ll * hsh[i][l - 1] * pwMod[i][r - l + 1]) % hashMod[i];
            t = (t + hashMod[i]) % hashMod[i];
            res[i] = t;
        }
        return res;
    }
};

bool equal(const vector<int> &h1, const vector<int> &h2)
{
    assert(h1.size() == h2.size());
    for (unsigned i = 0; i < h1.size(); i++)
        if (h1[i] != h2[i])
            return false;
    return true;
}
string str;
StringWithHash s;

map<PII, int> mp;

int cmp(int i, int j)
{// log比较长度相同的字符串大小
    if(mp.find({i, j}) != mp.end())
        return mp[{i, j}];
    //二分比较字符串
    // str[i : i + n], str[j : j + n]
    int l = 0, r = n;
    int ans = -1;
    while(l <= r)
    {
        int mid = (l + r) / 2;
        auto check = [&](int x)
        {
            if(x == 0) //空集判相等
                return true;
            auto v1 = s.getHash(i + 1, i + x - 1 + 1);
            auto v2 = s.getHash(j + 1, j + x - 1 + 1);
            return equal(v1, v2);
        };
        if(check(mid))
        {//前mid是否完全相同
            //如果完全相同
            ans = mid;
            l = mid + 1;
        }
        else {
            //得更短
            r = mid - 1;
        }
    }
    // assert(ans >= 0);
    // debug(ans);
    if(ans == n)
        return mp[{i, j}] = 0;
    else {
        if(str[i + ans] < str[j + ans])
            return mp[{i, j}] = -1;
        else 
            return mp[{i, j}] = 1;
    }
}


void solve()
{
    mp.clear();
    int k;
    cin >> n >> k;
    cin >> str;
    str += str;

    s.init(); //多测
    for(auto &c : str)
        s.extend(c);
    

    vector<int> id(n);
    iota(id.begin(), id.end(), 0);

    //获取第k小的元素
    nth_element(id.begin(), id.begin() + k - 1, id.end(), [&](int i, int j)
    {
        int ans = cmp(i, j);
        if(ans == -1)
            return true;
        else 
            return false;
    });
    // sort(id.begin(), id.end(), [&](int i, int j)
    // {
    //     int ans = cmp(i, j);
    //     if(ans == -1)
    //         return true;
    //     else 
    //         return false;
    // });
    // cerr << cmp(0, 4) << el;
    // lop(i, 0, n)
    // {
    //     cerr << id[i] << ' ';
    // }
    string res = "";
    for(int i = id[k - 1]; i <= id[k - 1] + n - 1; i ++)
        res += str[i];
    cout << res << el;

}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    int T;
    cin >> T;
    while (T--)
    {
        solve();
    }
}

G、 三点共线

使用叉积法判断即可。

萌新小朋友也可以用 斜率法判断，复杂度 ，需要注意斜率不存在的情况。

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;

PII operator-(PII a, PII b)
{
    return {a.x - b.x, a.y - b.y};
}

int operator *(PII a, PII b)
{
    return a.x * b.y - a.y * b.x;
}

void solve()
{
    cin >> n;
    vector<PII> a(n + 1);
    rep(i, 1, n)
    {
        cin >> a[i].x >> a[i].y;
    }

    rep(i, 1, n)
    {
        rep(j, i + 1, n)
        {
            rep(k, j + 1, n)
            {
                if((a[i] - a[j]) * (a[i] - a[k]) == 0)
                {
                    cout << "Yes" << el;
                    return ;
                }
            }
        }
    }
    cout << "No" << el;
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}

H、讨论组

贪心，直接除以 下取整即可。

尽可能三个人一组，最后一组可能多出来

n = int(input())
print(n // 3)

I、市场

显然删除一个点 ，只会影响 ，其他部分的总和是不变的。

我们撤销掉（扣掉）原本的贡献 abs(a[i - 1] - a[i]) + abs(a[i] - a[i + 1])

加上新的贡献即可 abs(a[i - 1] - a[i + 1])

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef int LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;

void solve()
{
    cin >> n;
    vector<int> a(n + 2);
    rep(i, 1, n)
    {
        cin >> a[i];
    }
    a[n + 1] = 0;
    LL now = 0;
    LL res = 0;
    vector<LL> ans(n + 2);
    rep(i, 1, n + 1)
    {
        res += abs(a[i] - a[i - 1]);
    }
    // debug(res);
    rep(i, 1, n)
    {
        //不访问第a[i]
        //相当于a[i - 1], a[i + 1]
        LL last = abs(a[i - 1] - a[i]) + abs(a[i] - a[i + 1]);
        LL val = abs(a[i - 1] - a[i + 1]);
        ans[i] = res - last + val;
    }
    // ans[n] = res - abs(a[n - 1] - a[n]);
    rep(i, 1, n)
    {
        cout << ans[i] << " \n"[i == n];
    }
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}

J、 区间缩小

做法1

先说一下 DP 的做法

固定概率 。

设 表示区间 的最后结果的期望。

显然我们将这个区间平移 后，期望也会平移 。

• 所以只跟长度有关，我们只需要求解 这个区间的答案即可。

然后思考题意得 的后继，有 两种

• 如果暴力枚举所有后继，转移是平方的。

但是发现这个东西可以前缀和优化，每次区间长度加一后，转移的那些前驱也只会加上一两个。

• 所以复杂度是 的

当初的草稿我找不到了，勉强看一下代码吧（

• 或者可以先把 或 的 的做法写出来，
• 然后再优化为前缀和的形式

代码1：

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 998244353;
constexpr int INF = 0x3f3f3f3f;
const int inv2 = (md + 1) / 2;
int n, m;

LL fpow(LL a, LL b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1)
            res = res * a % md;
        a = a * a % md;
        b >>= 1;
    }
    return res;
}

LL add(LL a, LL b)
{
    return (a + b) % md;
}
LL mul(LL a, LL b)
{
    return a * b % md;
}
LL addNorm(LL &a)
{
    if(a >= md)
        a -= md;
}
LL norm(LL &a)
{
    a %= md;
}

LL f[N], g[N];
LL sum[N];
void solve()
{
    int x;
    cin >> n >> x;
    f[1] = 1;
    g[1] = 1;
    sum[1] = f[1];
    LL sumI = 1;
    LL p = x * fpow(100, md - 2) % md;
    LL np = 1 - p;
    // swap(p, np);
    rep(i, 2, n)
    {
        LL inv = fpow(i, md - 2);
        LL A = sum[i - 1] * np % md * inv % md;
        LL B = (sum[i - 1] + sumI) % md;
        B = B * p % md * inv % md;
        f[i] = (A + B) % md;
        f[i] = f[i] * i % md * fpow(i - 1, md - 2) % md;

        sum[i] = sum[i - 1] + f[i];
        sum[i] %= md;

        // f[]
        sumI = (sumI + i) % md;
    }
    // 1/i * p 的概率，令l为l
    // 1/i * (1-p) 的概率，令r为r
    if(f[n] < 0)
        f[n] += md;
    cout << f[n] << el;
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}

做法2

进一步的，还有 的做法

• 答案就是一个公式
• 为

将 DP 的每次长度增加的贡献，继续展开计算出来，就可以得到每次的贡献为常数 。

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 998244353;
constexpr int INF = 0x3f3f3f3f;
int n, m;

LL fpow(LL a, LL b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1)
            res = res * a % md;
        a = a * a % md;
        b >>= 1;
    }
    return res;
}

void solve()
{
    int x;
    cin >> n >> x;
    LL p = 1LL * x * fpow(100, md - 2) % md;
    int ans = (1 + 1LL * (n - 1) * p % md) % md;
    cout << ans << el;
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}

K、 数字三角形

二进制构造即可

每行都是 和 交替，第 行想象为第 个二进制位（二进制从 位开始算），第一层没有用（类似trie树的根）

二进制覆盖所有的整数，这样总能选择到需要的数字

不过，输出的是具体的值，第 行，我们还是变成对应的 ​ 的幂次方

向左走向右走类似杨辉三角那样

#include <bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << x << '\n';
#define bd cerr << "----------------------" << el;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define lop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define cmax(a, b) a = max(a, b)
#define cmin(a, b) a = min(a, b)
#define x first
#define y second
#define db double

typedef long long LL;
typedef pair<int, int> PII;

constexpr int N = 2e6 + 10, md = 1e9 + 7;
constexpr int INF = 0x3f3f3f3f;

int n, m;
int pw[27];
void solve()
{
    cin >> n;
    vector<int> a(n + 1);
    rep(i, 1, n)
    {
        cin >> a[i];
    }
    int mx = *max_element(a.begin() + 1, a.begin() + n + 1);

    int e = 1;
    int cnt = 0;
    while(e <= mx){
        e <<= 1;
        cnt ++;
    }
    e >>= 1;
    cnt --;

    pw[0] = 1;
    rep(i, 1, 26)
    {
        pw[i] = pw[i - 1] * 2;
    }
    
    //第0层超级跟，相当于trie的根是空的
    //第i层，选择2^{i-1}这个二进制对应的数

    // 最多到第2 ^{cnt}
    // 也就是 cnt + 1 层

    
    // 2 ** cnt = e <= mx
    int len = cnt + 1;
    vector ans(cnt + 2, vector<int>());
    rep(i, 0, len)
    {
        ans[i].resize(i + 1, 0);
        ans[i][0] = 0;
        rep(j, 1, i)
        {
            if(j & 1)
                ans[i][j] = 1;
            else 
                ans[i][j] = 0;
        }        
    }
    cout << cnt + 2 << el;
    lop(i, 0, len + 1)
    {
        lop(j, 0, ans[i].size())
        {
            if(j > 0)
                cout << ' ';
            if(ans[i][j])
            {
                cout << pw[i - 1];
            }
            else {
                cout << 0;
            }
        }
        cout << el;
    }
    vector<string> res;
    rep(i, 1, n)
    {
        int pos = 0;
        int y = 0;
        int val = a[i];
        string now;
        rep(j, 1, len)
        {
            if(val >> (j - 1) & 1)
            {//这一位是1
                if(ans[j][y])
                {
                    now += 'L';
                }
                else {
                    now += 'R';
                    y ++;
                }
            }
            else {
                //这一位是0
                if(!ans[j][y])
                {
                    now += 'L';
                }
                else {
                    now += 'R';
                    y ++;
                }
            }
        }
        res.push_back(now);
    }
    for(auto &s : res)
    {
        cout << s << el;
    }
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    solve();
}