题意:
@#¥&《?…%&…¥&#¥%%%#¥%&……#……%……&*%……&*¥…&%&¥…%#¥%……( 一大堆废话)
求
根据费马小定理,可以转化为求
关键就在于求那个指数。首先这个数比较大,卢卡斯开不了这么大的数组,那怎么办呢???我们可以看到999911658不是一个质数,因式分解可以得到999911658=2 x 3 x 4679 x 35617;我们就可以得到以下同余方程组
x就是我们要求的那个指数
用中国剩余定理解这个方程得到x
不会的同学可以跟着我一起复习一下:
已知:
上面那张图,假设有k项
我们令
M=a1∗a2∗...∗ak
x=(M/ai)∗bi∗inv(M/ai)
其中逆元是 mod(ai)意义下的逆元
这里看不懂的可以找别的博客看看
最后用快速幂求下G的x次方mod999911659就ok
注意,如果G==999911659要特判。
#include<cstdio>
#include<queue>
#include<algorithm>
#include<vector>
#include<cstring>
#include<cmath>
using namespace std;
#define maxn 100005
#define inf 0x3f3f3f3f
#define ll long long
#define mod 999911658
ll f[maxn];
ll b[4],a[4]={2,3,4679,35617};
void init(ll x){
f[0] = 1;
for (int i=1;i<=x;++i)f[i]=f[i-1]*i%x;
}
ll fastpow(ll x,ll y,ll p){
ll ans=1;
ll res=x;
while(y){
if(y&1)ans=(ans*res)%p;
res=(res*res)%p;
y>>=1;
}
return ans;
}
ll C(ll n,ll m,ll p){
if(n<m) return 0;
return f[n]*fastpow(f[m],p-2,p)%p*fastpow(f[n-m],p-2,p)%p;
}
ll lucas(ll n,ll m,ll p){
if(n<m) return 0;
if(!n) return 1;
return lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}
ll factor[maxn];
ll cnt;
ll getfactor(ll x){
cnt=0;
memset(factor,0,sizeof(0));
for(ll i=1;i*i<x;i++){
if(x%i==0){
factor[cnt++]=i;
factor[cnt++]=x/i;
}
}
ll xx=sqrt(x);
if(xx*xx==x)factor[cnt++]=xx;
return 0;
}
ll ans=0;
void chinses(){
for(ll i=0;i<4;i++){
ans=(ans+b[i]*(mod/a[i])%mod*fastpow(mod/a[i],a[i]-2,a[i]))%mod;
}
}
int main(){
ll n,g;
scanf("%lld %lld",&n,&g);
if(g%(mod+1)==0){
printf("0\n");
return 0;
}
getfactor(n);//得到这个n的所有约数
for(int i=0;i<4;i++){//对每个a[i]取模下求出那个b[i];
init(a[i]);
for(int j=0;j<cnt;j++){
b[i]=b[i]+lucas(n,factor[j],a[i])%a[i];
}
}
chinses();//中国剩余定理
printf("%lld\n",fastpow(g,ans,mod+1));
return 0;
}




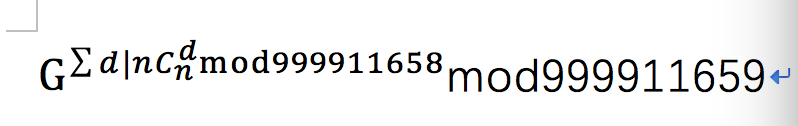
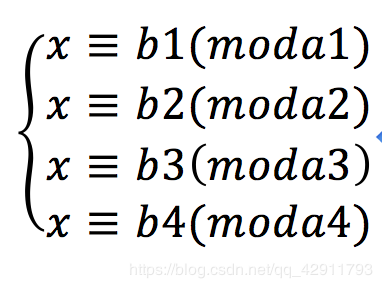

 京公网安备 11010502036488号
京公网安备 11010502036488号