http://acm.hdu.edu.cn/showproblem.php?pid=6482
Problem Description
WNJXYK hates Destinys so that he does not want to meet him at any time. Luckily, their classrooms and dormitories are at different places. The only chance for them to meet each other is on their way to classrooms from dormitories.
To simple this question, we can assume that the map of school is a normal rectangular 2D net. WNJXYK’s dormitory located at (0,y1) and his classroom located at (x1,0). Destinys’s dormitory located at (0,y2) and his classroom is located at (x2,0). On their way to classrooms, they can do two kinds of movement : (x,y)->(x,y-1) and (x,y)->(x+1,y).
WNJXYK does not want to meet Destinys so that he thinks that it is not safe to let his path to classroom from dormitory has any intersect point with Destinys ‘s. And then he wonders how many different paths for WNJXYK and Destinys arriving their classrooms from dormitories safely.
题意:求 (0,y1)−>(x1,0),(0,y2)−>(x2,0)的不相交路径的方案数。
思路:
按照Lindström–Gessel–Viennot定理(维基:https://en.wikipedia.org/wiki/Lindström–Gessel–Viennot_lemma)
对于一张无边权的DAG图,给定n个起点和对应的n个终点,n条不相交路径的方案数为:
其中 ai 代表路径的起点 bi 代表路径的终点, e(ai,bj) 代表ai到bj的方案数。
对于这道题,就是n=2的情形。
答案是:
| e(a1,b1) e(a1,b2) |
| e(a2,b1) e(a2,b2) |
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
int T,x[3],y[3];
ll fac[200000+100];
ll pow_mod(ll a,ll n)
{
if(n==0)return 1;
ll x=pow_mod(a,n/2);
x=x*x%mod;
if(n&1)x=x*a%mod;
return x;
}
ll c(ll n,ll m)
{
return fac[n]*pow_mod(fac[m],mod-2)%mod*pow_mod(fac[n-m],mod-2)%mod;
}
int main()
{
cin>>T;
fac[0]=1;
for(int i=1;i<=200000;i++)fac[i]=fac[i-1]*i%mod;
while(T--)
{
cin>>x[1]>>x[2]>>y[1]>>y[2];
cout<<(c(x[1]+y[1],x[1])*c(x[2]+y[2],x[2])%mod-c(x[1]+y[2],x[1])*c(x[2]+y[1],x[2])%mod+mod)%mod<<endl;
}
return 0;
}



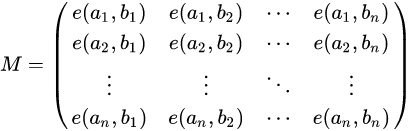

 京公网安备 11010502036488号
京公网安备 11010502036488号