在学习对抗神经网络Gan的时候出现里这个概念，在网上找里一些博客，理解了一下这个概念。
卷积：
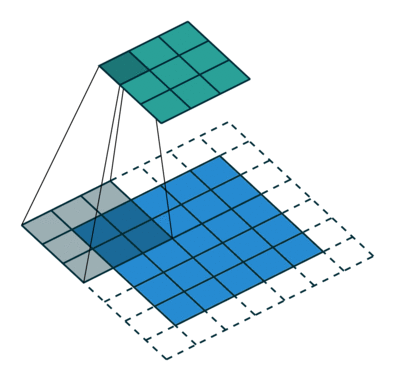
就是这个图啦，其中蓝色部分是输入的feature map，然后有3*3的卷积核在上面以步长为2的速度滑动，可以看到周围还加里一圈padding，用更标准化的参数方式来描述这个过程：
二维的离散卷积(N=2)
方形的特征输入( i 1 = i 2 = i )
方形的卷积核尺寸( k 1 = k 2 = k )
每个维度相同的步长( s 1 = s 2 = s )
每个维度相同的padding( p 1 = p 2 = p )

( i = 5 , k = 3 , s = 2 , p = 1 ) ,输出特征尺寸 o 1 = o 2 = o
其中，卷积层输入特征与输出特征尺寸和卷积核参数的关系为：
o = ( f l o o r ) [ i + 2 p − k s ] + 1
反卷积

考虑一下这个图，其中的参数描述是:(i=4,k=3,s=1,p=0),输出o=2。
对于这个运算,我们把3*3的卷积核展开成如下图所示的[4,16]的稀疏矩阵,其中非0元素 w i j 表示卷及核的第i行和第j列。


然后再把4*4的输入特征转换成[16,1]的矩阵X，那么Y=CX则是一个[4,1]的输出特征矩阵，把它重新排列2×2的输出特征就得到最终的结果，从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。通过上述的分析，我们已经知道卷积层的前向操作可以表示为和矩阵C相乘，那么我们很容易得到卷积层的反向传播就是和C的转置相乘。
反卷积的作用：噪声升维，上采样，从低维度进入高维度，比直接给定高维度随机形更强，这样就可以通过修改转置conv kernel去梯度下降出网络超参数

参考博客：http://blog.csdn.net/xiaojiajia007/article/details/75041651