1. 线性时不变系统对复指数信号的响应
在研究 LTI(Linear and Time-invariant System)系统时,将信号表示成基本信号的线性组合是很有利的,但这些基本信号应该具有以下两个性质:
- 由这些基本信号能够构成相当广泛的一类有用信号;
- LTI 系统对每一个基本信号的响应应该十分简单,以使得系统对任意输入信号的响应有一个很方便的表示式。
傅里叶分析的很多重要价值都来自于这一点,即连续和离散时间复指数信号集都具有上述两个性质,即连续时间的 est 和离散时间的 zn,其中 s 和 z 都是复数。
在研究 LTI 系统时,复指数信号的重要性在于这样一个事实,即一个 LTI 系统对复指数信号的响应也是同样一个复指数信号,不同的只是幅度上的变化,也就是说:
连续时间:est→H(s)est
离散时间:zn→H(z)zn
这里 H(s) 或 H(z) 是一个复振幅因子,一般来说是复变量 s 或 z 的函数。一个信号,若系统对该信号的输出响应仅是一个常数乘以输入,则称该信号为系统的特征函数,而幅度因子称为系统的特征值。
现考虑一个单位冲激响应为 h(t) 的连续时间 LTI 系统,对任意输入 x(t),可由卷积积分来确定输出,若令 x(t)=est,则有
y(t)=∫−∞+∞h(τ)x(t−τ)dτ=∫−∞+∞h(τ)es(t−τ)dτ=est∫−∞+∞h(τ)e−sτdτ(1)
假设 (1)式右边的积分收敛,于是系统对 x(t) 的响应就为
y(t)=H(s)est(2)
式中 H(s) 是一个复常数,其值决定于 s,并且它与系统单位冲激响应的关系为
H(s)=∫−∞+∞h(τ)e−sτdτ(3)
可以完全用并行的方式证明,复指数序列也是离散时间 LTI 系统的特征函数。这就是说单位脉冲响应为 h[n] 的 LTI 系统,其输入序列为
x[n]=zn(4)
式中 z 为某一复数,由卷积和可以确定系统的输出为
y[n]=k=−∞∑+∞h[k]x[n−k]=k=−∞∑+∞h[k]zn−k=znk=−∞∑+∞h[k]z−k(5)
假设 (5)式右边的求和收敛,于是系统对 x[n] 的响应就为
y[n]=H(z)zn(6)
式中 H(z) 是一个复常数,为
H[z]=k=−∞∑+∞h[k]z−k(7)
针对更一般的情况,若一个连续时间 LTI 系统的输入表示成复指数的线性组合,即
x(t)=k∑akeskt(8)
那么输出就一定是
y(t)=k∑akH(sk)eskt(9)
对于离散情况,完全类似,若一个离散时间 LTI 系统的输入表示成复指数的线性组合,即
x[n]=k∑akzkn(10)
那么输出就一定是
y[n]=k∑akH(zk)zkn(11)
2. 连续时间周期信号的傅里叶级数表示
2.1. 成谐波关系的复指数信号的线性组合
周期复指数信号
x(t)=ejω0t(12)
的基波频率为 ω0,基波周期 T=2π/ω0。与之有关的成谐波关系的复指数信号集就是
ϕk(t)=ejkω0t=ejk(2π/T)t,k=0,±1,±2,⋅⋅⋅(13)
这些信号中的每一个都有一个基波频率,它是 ω0 的倍数。因此每个信号对周期 T 来说都是周期的。于是,一个由成谐波关系的复指数信号线性组合形成的信号
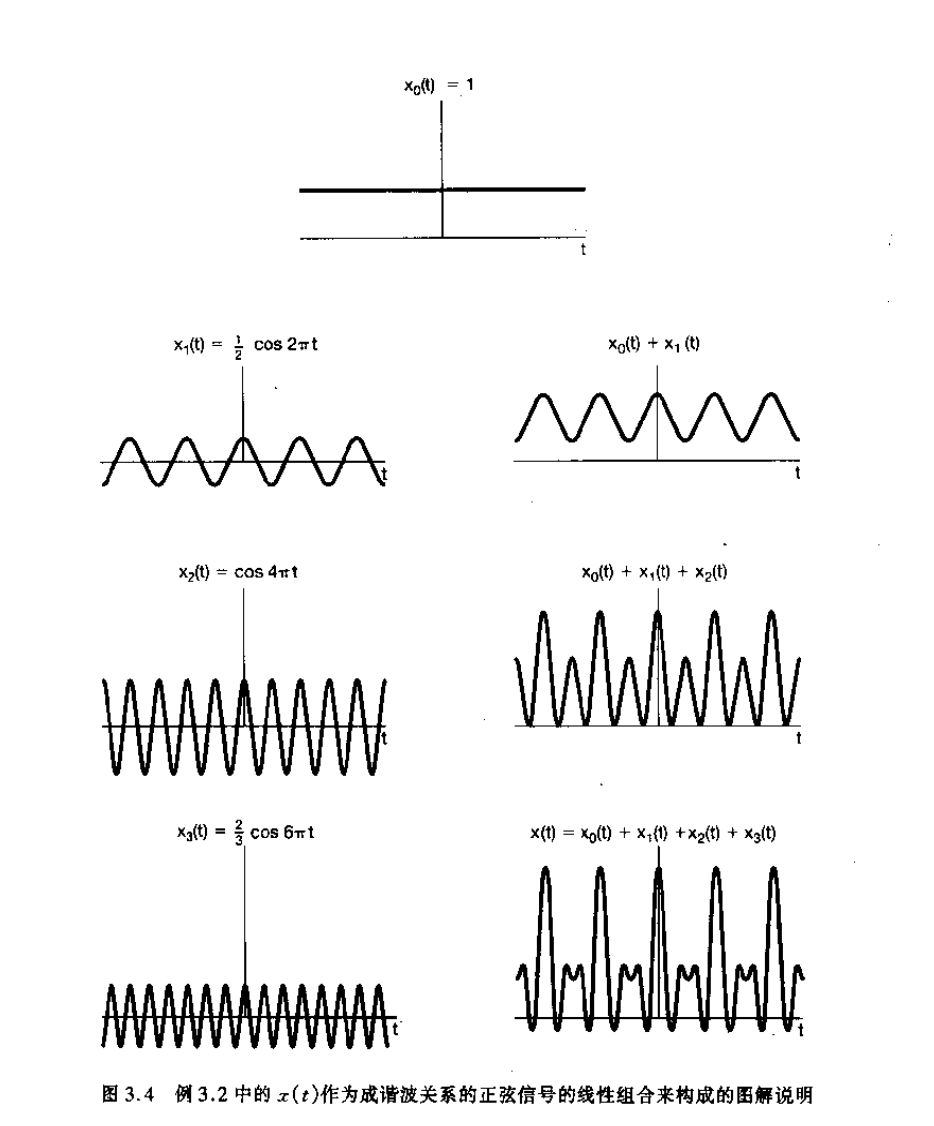
x(t)=k=−∞∑∞akejkω0t=k=−∞∑∞akejk(2π/T)t(14)
对周期 T 来说也是周期的。 在式(14)中, k=0 这一项是个常数, k=+1 和 k=−1这两项都有基波频率等于 ω0,两者合在一起称之为基波分量或称一次谐波分量。 k=+2 和 k=−2 这两项也是周期的,其频率是基波频率的两倍,称为二次谐波分量。一般来说, k=+N 和 k=−N 的分量称为第 N 次谐波分量。
一个周期信号表示成式(14)的形式,就称为傅里叶级数表示。

2.2. 连续时间周期傅里叶级数表示的确定
假设一个给定的周期信号能表示成式(14)的形式,这就需要一种办法来确定这些系数 ak,将式(14)两边各乘以 e−jnω0t,可得
x(t)e−jnω0t=k=−∞∑∞akejkω0te−jnω0t(15)
将上式两边从 0 到 T=2π/ω0对 t 积分,有
∫0Tx(t)e−jnω0tdt=∫0Tk=−∞∑∞akejkω0te−jnω0tdt(16)
这里 T 是 x(t) 的基波周期,以上就是在该周期内积分。将上式右边的积分和求和次序交换后得
∫0Tx(t)e−jnω0tdt=k=−∞∑∞ak∫0Tej(k−n)ω0tdt(17)
式(17)右边括号里的积分是很容易的,为此利用欧拉公式可得
∫0Tej(k−n)ω0tdt=∫0Tcos(k−n)ω0tdt+j∫0Tsin(k−n)ω0tdt(18)
对于 k̸=n, cos(k−n)ω0t 和 sin(k−n)ω0t都是周期函数,其基波周期为 (T/∣k−n∣)。现在做的积分是在 T 区间内进行,而 T 又一定是它们的基波周期 (T/∣k−n∣) 的整数倍。由于积分可以看做是被积函数在积分区间内所包括的面积,所以式(18) 右边的两个积分对于 k̸=n 来说,其值为 0;而对 k=n,式左边的被积函数是 1,所以其积分值为 T 。综合上述得到
∫0Tej(k−n)ω0tdt={T,0,k=nk̸=n(19)
这样式(17)的右边就变成了 Tan,因此有
an=T1∫0Tx(t)e−jnω0tdt(20)
另外,在求式(18)时我们仅仅用到了积分是在一个 T 的时间间隔内进行,而该 T 又是 cos(k−n)ω0t 和 sin(k−n)ω0t 周期的整数倍。因此,**如果是在任意 T 的间隔做积分,结果应该是相同的。**也就是说,若以 ∫T 表示在任意一个 T 间隔内的积分,则应该有
∫Tej(k−n)ω0tdt={T,0,k=nk̸=n(21)
因此
an=T1∫Tx(t)e−jnω0tdt(22)
上述过程可归结下:如果 x(t) 能表示成一组成谐波关系的复指数信号的线性组合,那么傅里叶级数中系数就由式(22)所确定,这一对关系就定义为一个周期连续信号的傅里叶计数。
x(t)=k=−∞∑∞akejkω0t=k=−∞∑∞akejk(2π/T)t
ak=T1∫Tx(t)e−jkω0tdt=T1∫Tx(t)e−jk(2π/T)tdt
第一个式子称为综合公式,第二个式子称为分析公式。系数 ak 往往称为 x(t) 的傅里叶级数系数或频谱系数。
2.3. 傅里叶级数的收敛
对于任何周期信号,我们总是能利用式(22)求得一组傅里叶系数。然而,在某些情况下式(22)的积分可能不收敛,也就是说求得的某些系数可能是无穷大。再者,即使求得的全部系数都是有限值,当把这些系数代入式(14)时所得到的无限项级数也可能不收敛于原信号。
狄里赫利条件:
-
在任何周期内, x(t) 必须绝对可积,即
∫T∣x(t)∣dt<∞(23)
这一条件保证了每一系数 ak 都是有限值,因为
∣ak∣⩽T1∫T∣x(t)ejkω0t∣dt=T1∫T∣x(t)∣dt(24)
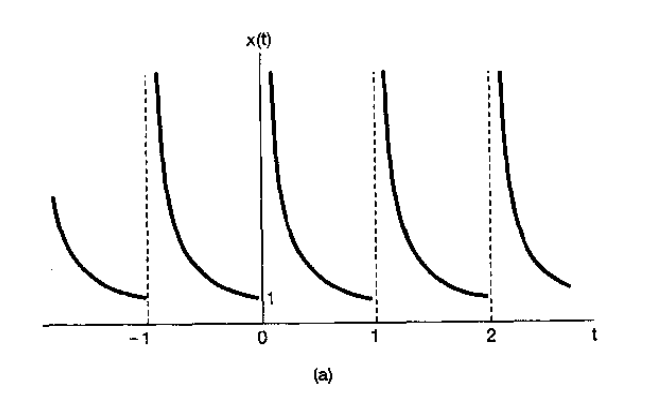
不满足狄里赫利第一条件的周期信号可以举例如下:
x(t)=t1,0<t⩽1(25)
-
在任意有限区间内, x(t) 具有有限个起伏变化,也就是说,在任何单个周期内, x(t) 的最大值和最小值的数目有限。
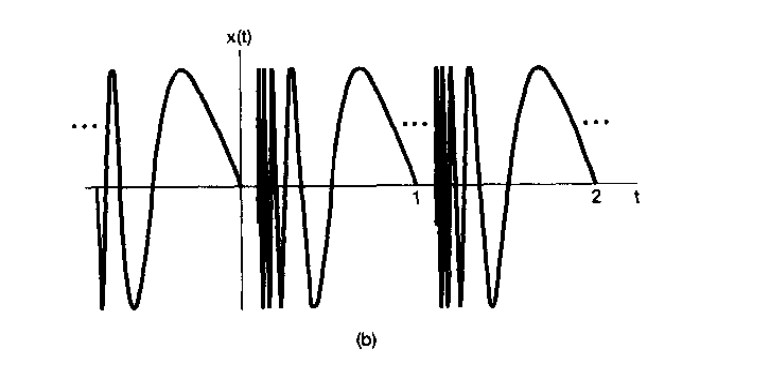
满足条件 1 而不满足条件 2 的一个函数是
x(t)=sin(t2π),0<t⩽1(26)
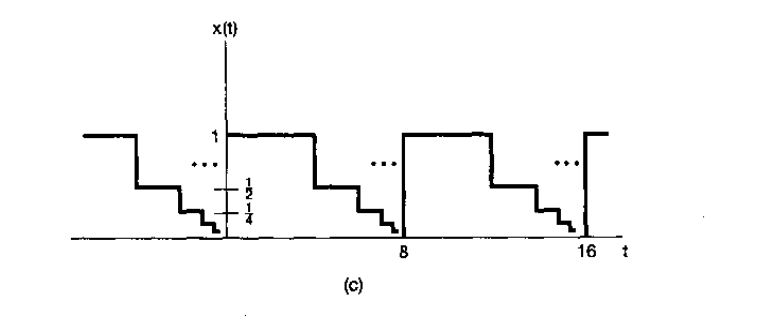
- 在 x(t) 的任何有限区间内,只有有限个不连续点,而且在这些不连续点上,函数都是有限值。
不满足条件 3 的一个例子如下所示,这个信号的周期为 T=8,它是这样组成的:后一个阶梯的高度和宽度都是前一个阶梯的一半。
2.4. 傅里叶级数的性质

3. 离散时间周期信号的傅里叶级数表示
3.1. 成谐波关系的复指数信号的线性组合
周期复指数信号
x[n]=ej(2π/N)n(27)
基波频率为 ω0=2π/N,基波周期为 N。与之有关的成谐波关系的复指数信号集就是
ϕk[n]=ejkω0n=ejk(2π/N)n,k=0,±1,±2,⋅⋅⋅(28)
这些信号中的每一个都有一个基波频率,它是 2π/N 的倍数。由式(28)给出的信号集中只有 N 个信号是不相同的,这是由于离散时间复指数信号在频率上相差 2π/N 的整数倍都是一样的缘故。因此有
ϕk[n]=ϕk+rN[n](29)
这就是说,当 k 变化一个的 N 整数倍时,就得到一个完全一样的序列。现在我们希望利用序列 ϕk[n] 的线性组合来表示更一般的周期序列,这样一个线性组合就有如下形式
x[n]=k∑akϕk[n]=k∑akejkω0n=k∑akejk(2π/N)n(30)
因为序列 ϕk[n] 只有在 k 的 N 个相继值的区间是不同的,因此,式(30)的求和仅仅需要包括 N 项。为了指出这一点,特将求和限表示成 k=<N>,即
x[n]=k=<N>∑akϕk[n]=k=<N>∑akejkω0n=k=<N>∑akejk(2π/N)n(31)
譬如说, k 即可以取 k=0,1,2,⋅⋅⋅⋅⋅⋅,N−1,也可以取 k=3,4,⋅⋅⋅⋅⋅⋅,N+2,不管怎样取,式(31)右边的求和都是一样的。式(31)称为离散时间傅里叶级数,而系数 则称为傅里叶级数系数。
3.2. 离散时间周期傅里叶级数表示的确定
离散时间傅里叶级数对就为
x[n]=k=<N>∑akejkω0n=k=<N>∑akejk(2π/N)n
ak=N1k=<N>∑x[n]e−jkω0n=N1k=<N>∑x[n]e−jk(2π/N)n
和连续时间周期信号一样,第一个式子称为综合公式,第二个式子称为分析公式。系数 ak 往往称为 x[n] 的频谱系数。
再回到式(31),我们看到若从 0 到 N−1 范围内取 k,则有
x[n]=a0ϕ0[n]+a1ϕ1[n]+⋅⋅⋅+aN−1ϕN−1[n](32)
相类似地,若从 1 到 N 范围内取 k,则有
x[n]=a1ϕ1[n]+a2ϕ2[n]+⋅⋅⋅+aNϕN[n](33)
因为 $ \phi_0[n] = \phi_N[n]$,将式(32)和式(33)作一比较,就可以得出 a0=aN。类似地,若 k 取任何一组 N 个相连的整数,就一定有
ak=ak+N(34)
这就是说,倘若我们考虑的 k 值多余 N 的话,那么 ak 的值必定以 N 为周期,周期性重复。
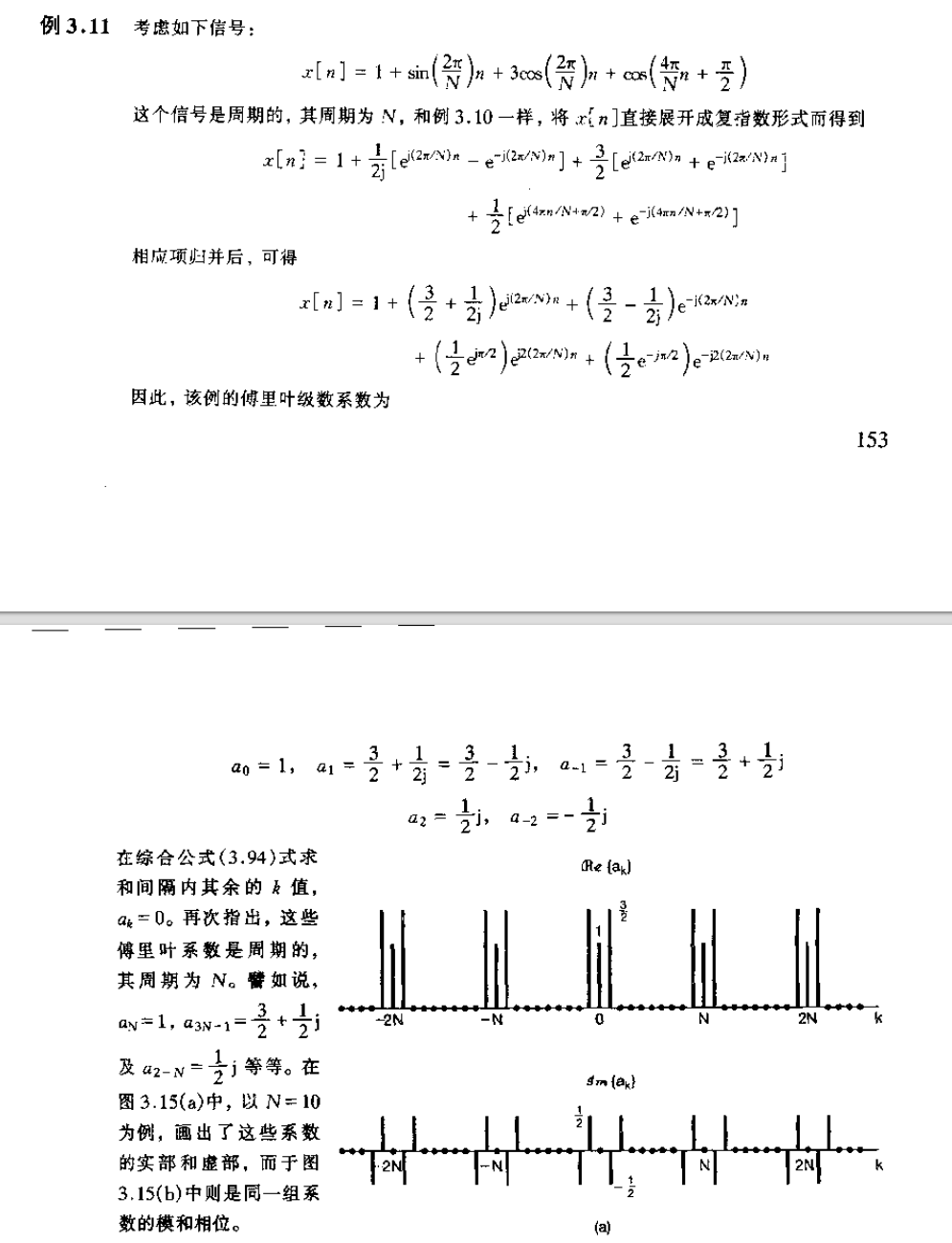
- 例 1
3.3. 离散时间傅里叶级数的性质

获取更多精彩,请关注「seniusen」!
















 京公网安备 11010502036488号
京公网安备 11010502036488号