描述
题目描述
这个题目是一道很不错的题目, 先是给了我们一颗树, 让我们求取树上最远点两个点的距离比如这样的一颗树
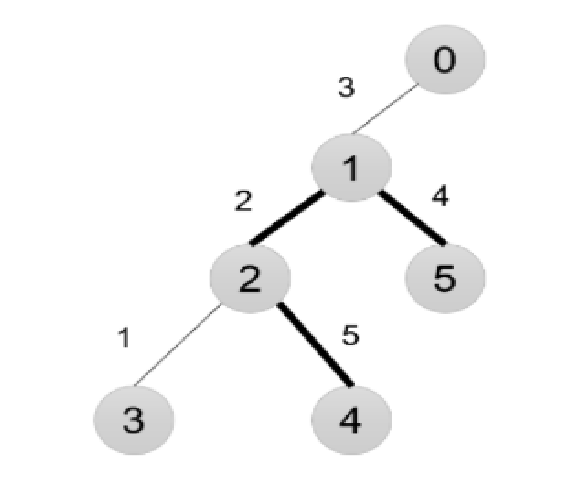
我们发现从到的权值是最大的, 所以我们输出他们的权值
然后我们仔细思考这个, 他没有规定我们应该是从哪一个点到哪一个点, 那么我们就是可以把他当成一个无向图来做, 这样我们就涉及到了建图
图论小课堂
首先我们建图, 一般来讲是两大类
第一种就是邻接矩阵, 这样其实就是开了一个二维数组来表示
那我么二维数组又是怎么表示的, 其实就是我们第一维到第二维就是代表了我们一个点, 到另一个点, 然后权值就是这个位置的值
第二种就是邻接表, 这个的实现方式有很多种, 其实本质就是一个个的链表, 然后我们直接开了很多个链表头, 然后每一个头可以拉出来一个链表
临界矩阵适合点少边多的图, 邻接表适合边少点多的图
然后邻接表其实就是这样的一个结构

然后每一个链表头代表这个点可以到他的链表里面的点
题解
解法一 : 暴力求解
实现思路
这个既然变成了一个无向图, 那么我们可以直接套一个Floyd的板子, 直接求取出来所有的路径长度, 然后找一个最长的就是我们的答案, 这个想法很简单写起来也很好写, 但是事实上这个时间复杂度和空间复杂度都是超标的
代码实现
class Solution {
public:
#define LL long long
void floyd(int& n, vector<vector<LL>>& G) {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
G[i][j] = min(G[i][j], G[i][k] + G[k][j]);
}
// Floyd的板子
int solve(int n, vector<Interval>& Tree_edge, vector<int>& Edge_value) {
vector<vector<LL>> G(n + 1, vector<LL>(n + 1, INT_MAX));
// 初始值设置为INT_MAX, 不开longlong计算会有溢出
for (int i = 0; i < Tree_edge.size(); i++) {
G[Tree_edge[i].start][Tree_edge[i].end] =
G[Tree_edge[i].end][Tree_edge[i].start] = Edge_value[i];
}
// 邻接矩阵建图
floyd(n, G);
int maxx = INT_MIN;
for (auto& it : G) {
for (auto& it1 : it)
if (it1 != INT_MAX) maxx = max(maxx * 1ll, it1);
}
// 找到我们的最大值
return maxx;
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们调用了Floyd算法, 这个三重循环
空间复杂度:
理由如下: 我们用的邻接矩阵存的图, 是点数的平方
解法二
实现思路
我们可以选取一个起点, 然后我们找到最长的路径, 得到终点之后, 我们再从终点进行第二次dfs, 这样找到的最长路就是我们的直径
然后我们可以想一下
如果我们从走到恰好就是我们最后的直径这个是最好的
如果不是的话, 那么我们从找, 我们可以保证一定是直径的一个端点, 然后我们找到另一个点假设是
然后我们可以直到, 和 一定有一段是重合的, 所以我们最后就是直径
代码实现
class Solution {
public:
void dfs(int cur, int pre, int sum, vector<vector<pair<int, int>>>& G, int &u, int &maxx) {
if (G[cur].size() == 1 and G[cur][0].first == pre) {
if (maxx < sum) maxx = sum, u = cur;
// 如果更长久进行更新
return;
}
for (auto &it : G[cur]) {
if (it.first != pre) dfs(it.first, cur, sum + it.second, G, u, maxx);
// 遍历边上的点
}
}
int solve(int n, vector<Interval>& Tree_edge, vector<int>& Edge_value) {
vector<vector<pair<int, int>>> G(n);
for (int i = 0; i < Tree_edge.size(); i++) {
G[Tree_edge[i].start].emplace_back(Tree_edge[i].end, Edge_value[i]);
G[Tree_edge[i].end].emplace_back(Tree_edge[i].start, Edge_value[i]);
}
// 邻接表建图
int maxx = INT_MIN, u = -1;
dfs(0, -1, 0, G, u, maxx);
// 正向搜索
dfs(u, -1, 0, G, u, maxx);
// 得到最后的点反过来搜索
return maxx;
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们遍历了所有的点两次
空间复杂度:
理由如下: 邻接表存图是点数加边数的空间






 京公网安备 11010502036488号
京公网安备 11010502036488号