Sumdiv
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 18877 | Accepted: 4745 |
Description
Consider two natural numbers A and B. Let S be the sum of all natural divisors of A^B. Determine S modulo 9901 (the rest of the division of S by 9901).
Input
The only line contains the two natural numbers A and B, (0 <= A,B <= 50000000)separated by blanks.
Output
The only line of the output will contain S modulo 9901.
Sample Input
2 3
Sample Output
15
Hint
2^3 = 8.
The natural divisors of 8 are: 1,2,4,8. Their sum is 15.
15 modulo 9901 is 15 (that should be output).
The natural divisors of 8 are: 1,2,4,8. Their sum is 15.
15 modulo 9901 is 15 (that should be output).
Source
题意:给定两个正整数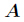
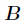

分析:很容易知道,先把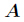
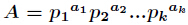
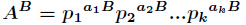
的所有因子和的表达式如下
所以我们有两种做法。第一种做法是二分求等比数列之和。
代码:
- #include <iostream>
- #include <string.h>
- #include <stdio.h>
- using namespace std;
- typedef long long LL;
- const int N = 10005;
- const int MOD = 9901;
- bool prime[N];
- int p[N];
- int cnt;
- void isprime()
- {
- cnt = 0;
- memset(prime,true,sizeof(prime));
- for(int i=2; i<N; i++)
- {
- if(prime[i])
- {
- p[cnt++] = i;
- for(int j=i+i; j<N; j+=i)
- prime[j] = false;
- }
- }
- }
- LL power(LL a,LL b)
- {
- LL ans = 1;
- a %= MOD;
- while(b)
- {
- if(b & 1)
- {
- ans = ans * a % MOD;
- b--;
- }
- b >>= 1;
- a = a * a % MOD;
- }
- return ans;
- }
- LL sum(LL a,LL n)
- {
- if(n == 0) return 1;
- LL t = sum(a,(n-1)/2);
- if(n & 1)
- {
- LL cur = power(a,(n+1)/2);
- t = (t + t % MOD * cur % MOD) % MOD;
- }
- else
- {
- LL cur = power(a,(n+1)/2);
- t = (t + t % MOD * cur % MOD) % MOD;
- t = (t + power(a,n)) % MOD;
- }
- return t;
- }
- void Solve(LL A,LL B)
- {
- LL ans = 1;
- for(int i=0; p[i]*p[i] <= A; i++)
- {
- if(A % p[i] == 0)
- {
- int num = 0;
- while(A % p[i] == 0)
- {
- num++;
- A /= p[i];
- }
- ans *= sum(p[i],num*B) % MOD;
- ans %= MOD;
- }
- }
- if(A > 1)
- {
- ans *= sum(A,B) % MOD;
- ans %= MOD;
- }
- cout<<ans<<endl;
- }
- int main()
- {
- LL A,B;
- isprime();
- while(cin>>A>>B)
- Solve(A,B);
- return 0;
- }
第二种方法就是用等比数列求和公式,但是要用逆元。用如下公式即可
因为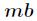
代码:
- #include <iostream>
- #include <string.h>
- #include <stdio.h>
- using namespace std;
- typedef long long LL;
- const int N = 10005;
- const int MOD = 9901;
- bool prime[N];
- int p[N];
- int cnt;
- void isprime()
- {
- cnt = 0;
- memset(prime,true,sizeof(prime));
- for(int i=2; i<N; i++)
- {
- if(prime[i])
- {
- p[cnt++] = i;
- for(int j=i+i; j<N; j+=i)
- prime[j] = false;
- }
- }
- }
- LL multi(LL a,LL b,LL m)
- {
- LL ans = 0;
- a %= m;
- while(b)
- {
- if(b & 1)
- {
- ans = (ans + a) % m;
- b--;
- }
- b >>= 1;
- a = (a + a) % m;
- }
- return ans;
- }
- LL quick_mod(LL a,LL b,LL m)
- {
- LL ans = 1;
- a %= m;
- while(b)
- {
- if(b & 1)
- {
- ans = multi(ans,a,m);
- b--;
- }
- b >>= 1;
- a = multi(a,a,m);
- }
- return ans;
- }
- void Solve(LL A,LL B)
- {
- LL ans = 1;
- for(int i=0; p[i]*p[i] <= A; i++)
- {
- if(A % p[i] == 0)
- {
- int num = 0;
- while(A % p[i] == 0)
- {
- num++;
- A /= p[i];
- }
- LL M = (p[i] - 1) * MOD;
- ans *= (quick_mod(p[i],num*B+1,M) + M - 1) / (p[i] - 1);
- ans %= MOD;
- }
- }
- if(A > 1)
- {
- LL M = MOD * (A - 1);
- ans *= (quick_mod(A,B+1,M) + M - 1) / (A - 1);
- ans %= MOD;
- }
- cout<<ans<<endl;
- }
- int main()
- {
- LL A,B;
- isprime();
- while(cin>>A>>B)
- Solve(A,B);
- return 0;
- }



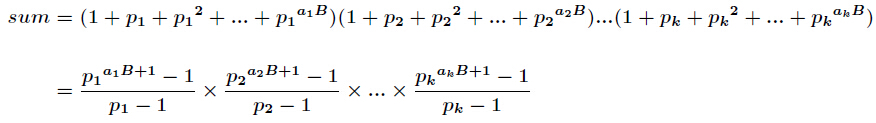
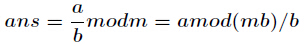

 京公网安备 11010502036488号
京公网安备 11010502036488号