1001 wa了两发,SPFA不熟练
1010 矩阵快速幂+分块,一看到这道题就有思路分块写,无奈能力对于n/i的特性还是不是很了解,调试了半天,花了好长时间才通过
1005 公式推出来了,化简不会了,对于容斥原理和莫比乌斯反演还是不够熟练
一个暑假过去了还是只会写水题,我好菜啊
1001
跑SPFA+set记录状态贼快,然后就没有然后了
#include <bits/stdc++.h>
#define mem(ar,num) memset(ar,num,sizeof(ar))
#define me(ar) memset(ar,0,sizeof(ar))
#define lowbit(x) (x&(-x))
#define Pb push_back
#define FI first
#define SE second
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define IOS ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int prime = 999983;
const int INF = 1e8;
const LL INFF =0x7FFFFFFFFFFFFFFF;
const double pi = acos(-1.0);
const double inf = 1e18;
const double eps = 1e-6;
const LL mod = 1e9 + 7;
LL qpow(LL a,LL b){LL s=1;while(b>0){if(b&1)s=s*a%mod;a=a*a%mod;b>>=1;}return s;}
LL gcd(LL a,LL b) {return b?gcd(b,a%b):a;}
int dr[2][4] = {1,-1,0,0,0,0,-1,1};
typedef pair<int,int> P;
const int maxn = 1e5+100;
vector<P> edge[maxn];
bool inq[maxn];
//int color[maxn];
int dis[maxn];
set<int> color[maxn];
int N,M;
void init(){
for(int i = 1;i <= N; ++i) edge[i].clear(),color[i].clear();
int u,v,w;
while(M--){
scanf("%d%d%d",&u,&v,&w);
edge[u].Pb(P(v,w));
edge[v].Pb(P(u,w));
}
}
int solve(){
me(inq);
me(color);
fill(dis+1,dis+N+1,INF);
dis[1] = 0;
queue<int> q;
q.push(1);
while(!q.empty()){
int u = q.front(); q.pop();
inq[u] = false;
// cout<<u<<endl;
for(int i = 0;i < edge[u].size(); ++i){
P &e = edge[u][i];
int t = 0;
if(color[u].find(e.SE) == color[u].end()) t++;
// cout<<t<<endl;
if(dis[u] + t <= dis[e.FI]){
if(dis[u] +t < dis[e.FI]) color[e.FI].clear();
if(color[e.FI].find(e.SE) != color[e.FI].end()) continue;
color[e.FI].insert(e.SE);
dis[e.FI] = dis[u]+t;
if(!inq[e.FI]){
q.push(e.FI);
inq[e.FI] = true;
}
}
}
}
if(dis[N] < INF) return dis[N];
else return -1;
}
int main(void)
{
while(cin>>N>>M){
init();
cout<<solve()<<endl;
}
return 0;
}
1002
字符串ST表
1003
不会QAQ
1004
概率题
1005
数论题,预处理+容斥
后面的部分可以用容斥做,令
倒着求F[K] 即可,复杂度O(nlog(n))
for(int i = N; i; --i){
F[i] = 1ll*(N/i)*(M/i);
// if(i == 1) cout<<F[i]<<endl;
for(int j = i+i;j <= N; j += i)
F[i] -= F[j];
}
#include <bits/stdc++.h>
#define mem(ar,num) memset(ar,num,sizeof(ar))
#define me(ar) memset(ar,0,sizeof(ar))
#define lowbit(x) (x&(-x))
#define pb push_back
#define FI first
#define SE second
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define IOS ios::sync_with_stdio(false)
#define DEBUG cout<<endl<<"DEBUG"<<endl;
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int prime = 999983;
const int INF = 0x7FFFFFFF;
const LL INFF =0x7FFFFFFFFFFFFFFF;
const double pi = acos(-1.0);
const double inf = 1e18;
const double eps = 1e-6;
// const LL mod = 1e9 + 7;
// LL qpow(LL a,LL b,LL mod){LL s=1;while(b>0){if(b&1)s=s*a%mod;a=a*a%mod;b>>=1;}return s;}
LL gcd(LL a,LL b) {return b?gcd(b,a%b):a;}
int dr[2][4] = {1,-1,0,0,0,0,-1,1};
// typedef pair<int,int> p;
const int maxn = 1e6+1000;
LL F[maxn],phi[maxn], inv[maxn];
LL N,M,P;
void init(int n){
for(int i = 1;i <= n; ++i) phi[i] = i;
for(int i = 2;i <= n; ++i){
if(i == phi[i]){
for(int j = i; j <= n; j += i) phi[j] = phi[j]/i*(i-1);
}
}
}
void init2(void){
inv[1] = 1;
for(int i = 2;i <= N; ++i)
inv[i] = (P - P/i*inv[P%i]%P)%P;
for(int i = N; i; --i){
F[i] = 1ll*(N/i)*(M/i);
// if(i == 1) cout<<F[i]<<endl;
for(int j = i+i;j <= N; j += i)
F[i] -= F[j];
}
//cout<<F[1]<<endl;
// DEBUG
/* for(int i = 1;i <= N; ++i) cout<<F[i]<<" "; cout<<endl; int FF[100]; me(FF); for(int i = 1;i <= N; ++i) for(int j = 1;j <= M; ++j) FF[gcd(i,j)]++; for(int i = 1;i <= N; ++i) cout<<FF[i]<<" "; cout<<endl;*/
}
LL solve(){
init2();
LL ans = 0;
for(LL i = 1;i <= N; ++i){
ans += (LL)i*inv[phi[i]]%P*(F[i]%P)%P;
assert(ans >= 0);
ans %= P;
}
// LL ans2 = 0;
/* DEBUG for(int i = 1;i <= N; ++i){ for(int j = 1;j <= M; ++j) ans2 += gcd(i,j)*inv[phi[gcd(i,j)]]%P; } ans2 %= P; if(ans2 != ans) { cout<<"ERROR"<<" "<<N<<" "<<M<<" "<<P<<endl; cout<<ans<<" "<<ans2<<endl; }*/
return ans%P;
}
// #define Debug
int main(void)
{
#ifdef Debug
freopen("input.txt","r",stdin);
freopen("output1.txt","w+",stdout);
#endif
init(maxn-1);
int T;
cin>>T;
while(T--){
cin>>N>>M>>P;
if( N < M) swap(N,M);
cout<<solve()<<endl;
}
return 0;
}
1006
异或+dp
1007
并查集+线段树
1008
LCA+树状数组
1009
LCT模板题
1010
分块+快速幂
#include <bits/stdc++.h>
#define mem(ar,num) memset(ar,num,sizeof(ar))
#define me(ar) memset(ar,0,sizeof(ar))
#define lowbit(x) (x&(-x))
#define Pb push_back
#define FI first
#define SE second
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define IOS ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int prime = 999983;
const int INF = 0x7FFFFFFF;
const LL INFF =0x7FFFFFFFFFFFFFFF;
const double pi = acos(-1.0);
//const double inf = 1e18;
const double eps = 1e-6;
const LL mod = 1e9 + 7;
//LL qpow(LL a,LL b){LL s=1;while(b>0){if(b&1)s=s*a%mod;a=a*a%mod;b>>=1;}return s;}
LL gcd(LL a,LL b) {return b?gcd(b,a%b):a;}
int dr[2][4] = {1,-1,0,0,0,0,-1,1};
//typedef pair<int,int> P;
LL A,B,C,D,P,N;
const int maxn = 4;
int n = 3;
struct Matrix{
Matrix(){ init();};
long long a[maxn][maxn];
void init(void)
{
memset(a,0,sizeof(a));
}
};
void print(const Matrix &a)
{
for(int i = 1;i <= n; ++i,cout<<endl)
for(int j= 1;j <=n; ++j)
cout<<a.a[i][j]<<" ";
}
Matrix operator*(Matrix a,Matrix b)
{
Matrix c;
c.init();
for(int i = 1;i <= n; ++i)
{
for(int j = 1;j <= n; ++j)
{
for(int k = 1;k <= n; ++k)
{
c.a[i][j] += a.a[i][k] * b.a[k][j];
c.a[i][j] %= mod;
}
}
}
// print(c);
return c;
}
Matrix qpow(Matrix a,long long b)
{
Matrix ans;
for(int i = 1;i <= n;++i)
ans.a[i][i] = 1;
// for(int j = )
while(b > 0)
{
if(b & 1)
ans = ans*a;
a = a*a;
b >>= 1;
}
return ans;
}
const int MAXN = 2e5+10;
LL F[MAXN];
LL solve(){
scanf("%lld %lld %lld %lld %lld %lld",&A,&B,&C,&D,&P,&N);
Matrix M;
if(N==1) return A;
if(N==2) return B;
F[1] = A;
F[2] = B;
LL m = sqrt(P);
for(int i = 3; i <= N&&i < MAXN; ++i){
F[i] = C*F[i-2]%mod+D*F[i-1]%mod+P/i;
F[i] %= mod;
}
if(N < MAXN) return F[N];
M.a[1][1] = F[MAXN-1],M.a[1][2] = F[MAXN-2];
Matrix MM;
MM.a[1][1] = D;
MM.a[2][1] = C;
MM.a[3][1] = 1;
MM.a[1][2] = MM.a[3][3] = 1;
int i;
LL com;
for( i = MAXN;i <= P&&i <= N; ){
com = P/i;
LL cc = P/com;
LL exp = P/com-i+1;
// cout<<exp<<endl;
M.a[1][3] = com;
exp = min(exp,N-i+1);
Matrix tmp = qpow(MM,exp);
// print(M);
// print(tmp);
M = M*tmp;
// print(M);
// cout<<exp<<endl;
i += exp;
}
// cout<<"i ="<<i<<endl;
if(i > N) return M.a[1][1];
com = 0;
M.a[1][3] = com;
LL exp = N-i+1;
Matrix tmp = qpow(MM,exp);
// print(M);
M = M*tmp;
// print(tmp);
// print(M);
return M.a[1][1]%mod;
}
int main(void)
{
int T;
cin>>T;
while(T--){
printf("%lld\n",solve());
}
return 0;
}
1011
优先队列+IO优化
#include <bits/stdc++.h>
#define mem(ar,num) memset(ar,num,sizeof(ar))
#define me(ar) memset(ar,0,sizeof(ar))
#define lowbit(x) (x&(-x))
#define Pb push_back
#define FI first
#define SE second
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define IOS ios::sync_with_stdio(false)
#define DEBUG cout<<endl<<"DEBUG"<<endl;
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int prime = 999983;
const int INF = 0x7FFFFFFF;
const LL INFF =0x7FFFFFFFFFFFFFFF;
const double pi = acos(-1.0);
const double inf = 1e18;
const double eps = 1e-6;
const LL mod = 1e9 + 7;
LL qpow(LL a,LL b){LL s=1;while(b>0){if(b&1)s=s*a%mod;a=a*a%mod;b>>=1;}return s;}
LL gcd(LL a,LL b) {return b?gcd(b,a%b):a;}
int dr[2][4] = {1,-1,0,0,0,0,-1,1};
typedef pair<int,int> P;
const int maxn = 1e5+100;
const int maxk = 6;
int N,K;
int ch[maxn][maxk];
int C[maxn][maxk];
LL V[maxk];
namespace io {
const int L = 1 << 20 | 1;
char ibuf[L], *iS, *iT, c, obuf[L], *oS = obuf, *oT = obuf + L - 1, qu[55]; int f, qr;
#ifdef whzzt
#define gc() getchar()
#else
#define gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, L, stdin), iS == iT ? EOF : *iS ++) : *iS ++)
#endif
template <class I>
inline void gi (I &x) {
for (f = 1, c = gc(); c < '0' || c > '9'; c = gc()) if (c == '-') f = -1;
for (x = 0; c <= '9' && c >= '0'; c = gc()) x = x * 10 + (c & 15); x *= f;
}
inline void flush () {
fwrite (obuf, 1, oS - obuf, stdout);
}
inline void putc (char x) {
*oS ++ = x;
if (oS == oT) flush (), oS = obuf;
}
template <class I>
void print (I x) {
if (!x) putc ('0'); if (x < 0) putc ('-'), x = -x;
while (x) qu[++ qr] = x % 10 + '0', x /= 10;
while (qr) putc (qu[qr --]);
}
struct io_ff { ~io_ff() { flush(); } } _io_ff_;
}
using io :: gi;
using io :: putc;
using io :: print;
void Add(int i){
for(int j = 0;j < K; ++j) V[j] += C[i][j];
}
//#define Debug
int main(void)
{
#ifdef Debug
freopen("1.in","r",stdin);
// freopen("output.txt","w+",stdout);
#endif
int T;gi(T);
// cin>>T;
// cout<<T<<endl;
while(T--){
gi(N),gi(K);
// cout<<N<<K<<endl;
// cout<<N<<" "<<
for(int i = 0;i < K; ++i)
// scanf("%lld",&V[i]);
gi(V[i]);
// for(int i = 0;i < K; ++i) cout<<V[i]<<endl;
rep(i,1,N+1){
rep(j,0,K){
// scanf("%d",&ch[i][j]);
gi(ch[i][j]);
}
rep(j,0,K)
// scanf("%d",&C[i][j]);
gi(C[i][j]);
// DEBUG;
}
// DEBUG;
// DEBUG;
priority_queue<P,vector<P>,greater<P> > q[5];
for(int i = 1;i <= N; ++i) q[0].push(P(ch[i][0],i));
bool t = true;
// DEBUG;
// DEBUG;
while(t){
t = false;
for(int i = 0;i < K-1; ++i){
while(!q[i].empty()&&q[i].top().FI <= V[i]){
t = true;
int e = q[i].top().SE;
q[i+1].push(P(ch[e][i+1],e));
q[i].pop();
}
}
while(!q[K-1].empty()&&q[K-1].top().FI <= V[K-1]){
Add(q[K-1].top().SE);
q[K-1].pop();
t = true;
}
}
int ans = N;
for(int i = 0;i < K; ++i)
ans -= q[i].size();
// IO::print(ans);
printf("%d\n",ans);
for(int i = 0;i < K; ++i) printf("%lld%c",V[i]," \n"[i==K-1]);
}
return 0;
}



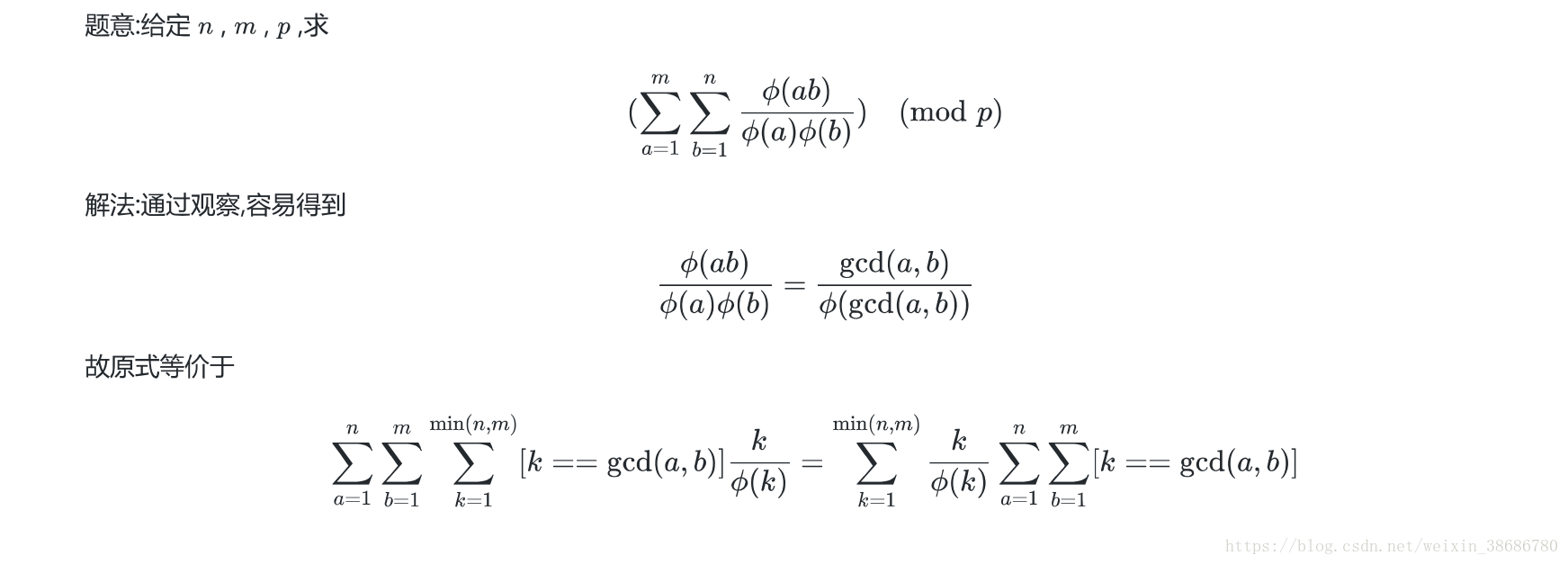

 京公网安备 11010502036488号
京公网安备 11010502036488号