Description

Priestess of the Moon (PotM) is a very interesting *** the game Defense of the Ancients (DotA). Here is the official description of PotM:

“A matriarch and high priestess of Elune’s blessed order, Mirana Nightshade serves as a light in darkness for the front line of the Sentinel ranks, raining arrows and falling stars alike upon the shambling undead masses of the Undead Scourge, while her very presence is said to be so holy that it melts away the fatigue of nearby allies, giving them greater haste on the battlefield. In times of need however, she can fade herself and others around her into the safety of invisibility, making her a potent supporter matched by few.”

She has a very powerful skill named Elune’s Arrow. When she uses this ability, she fires an arrow to a location with deadly precision, dealing large damage and stunning the first unit it strikes. A powerful skill, but hard to manage, because the enemy never stands still waiting for your arrow, and you can’t change the angle after you fires the arrow. For the sake of simplicity, you can assume that the enemy’s body area is a circle with radius r0, the effective range of your arrow is also a circle with radius r1, and the enemy always runs in a straight line. Now, PotM is standing at (x1, y1), while the enemy’s position is (x0, y0). The enemy’s speed in both x and y directions can be represent by a vector (dx, dy). So, after t minutes, the enemy’s position will be (x0+dxt, y0+dyt). The speed of PotM’s arrow is v. If the effective range of the arrow touches the enemy’s body area, it will be considered a strike, just like the collision of two circles. Now PotM wants to strike the enemy as soon as possible, could you help her to determine the time which the arrow takes to strike the enemy?

Input

The first line of the input contains a single number T (T <= 100), indicating the number of cases.

Each case consists of 5 lines, and each line contains the following decimal numbers:

x0, y0 (the enemy’s initial position)
x1, y1 (PotM’s initial position)
dx, dy (speed vector of the enemy)
r0, r1 (radii of the circles of the enemy’s body and the effective range of the arrow)
v, (positive speed of the arrow)

There is a blank line between the cases.
Note: the initial distance between PotM and the enemy will be larger than r0+ r1.

Output

For each case, output the least time (in minutes) PotM needs to strike the enemy(accurate up to 4 decimal places). If PotM cannot strike the enemy, just output “Impossible” in one line.

Sample Input

2
0.0 0.0
4.0 0.0
1.0 0.0
1.0 1.0
2.0

0.0 0.0
300.0 400.0
-3.0 -4.0
1.0 1.0
5.0

Sample Output

0.6667
Impossible

题目大意：

平面中一个半径为r1的圆的圆心初始在(x1, y1)，以速度向量(dx, dy)运动，另一个半径为r0的圆的圆心初始在(x0, y0)，可以向任何方向以速度v运动，求最小的时间t使得两圆相撞(也就是相切)。

解题思路：

令(x0, y0)与(x1, y1)之间的距离为l，即 l = l= l= ( x 0 − x 1 ) 2 + ( y 0 − y 1 ) 2 \sqrt{ (x0-x1)^{2}+(y0-y1)^{2} } (x0−x1)2+(y0−y1)2 ​。
半径为r1的圆以速度向量(dx, dy)运动，即该圆沿向量(dx, dy)所在直线运动。

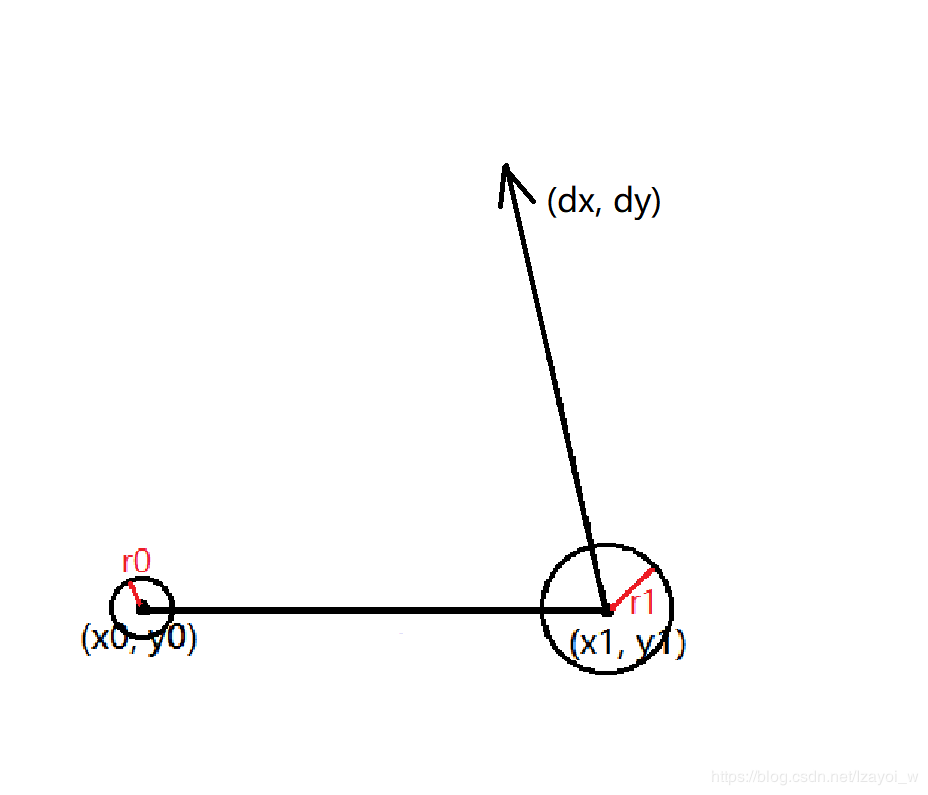
如图所示：

假设两圆相切时大圆位于图中的位置，小圆有可能在不同的位置与大圆相切，但它们的圆心距是恒定的，都是r0+r1，于是可以将两圆相切时小圆的圆心可能在的位置连起来，补全成为一个半径为r0+r1的圆，这个圆与大圆同心，它们的速度信息是一样的。
此时，问题就可以看成是在(x0, y0)处发射一个点，经过最短的时间击中那个半径为r0+r1的运动中的圆。而这个发射出的点可以经过的最短路径便是(x0, y0)与大圆圆心的连线。
如下图：设此三点分别为A、B、C，其对边分别为a、b、c
a的长度有两部分：从B点发射出的点的路径长度加上r0+r1
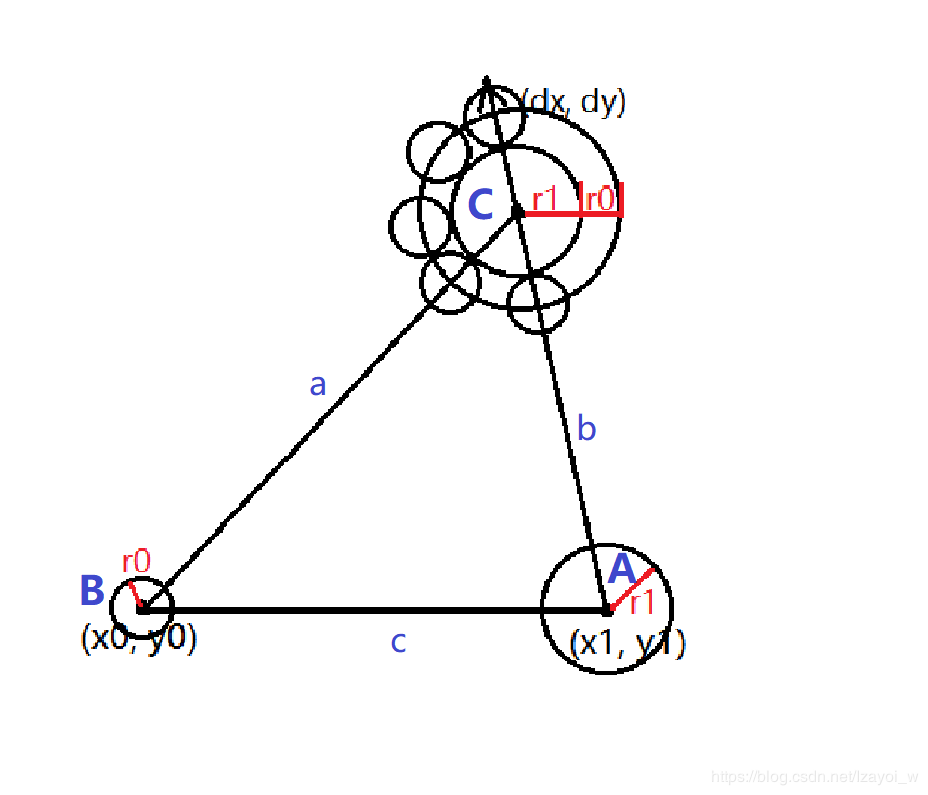
b的长度是B点和A点间的距离
c的长度是大圆圆心运动的路径长度
大圆和小圆运动的时间是相等的，设为t

那么，根据余弦定理： a 2 a^{2} a2 = = = b 2 + c 2 − 2 b c c o s A b^{2}+c^{2}-2bc cosA b2+c2−2bccosA

( v t + ( r 0 + r 1 ) ) 2 = ( x 0 − x 1 ) 2 + ( y 0 − y 1 ) 2 + ( d x 2 + d y 2 ) t 2 − 2 t [ ( x 0 − x 1 ) 2 + ( y 0 − y 1 ) 2 ] ( d x 2 + d y 2 ) ( x 0 − x 1 ) d x + ( y 0 − y 1 ) d y [ ( x 0 − x 1 ) 2 + ( y 0 − y 1 ) 2 ] ( d x 2 + d y 2 ) (vt+(r0+r1))^{2}=(x0-x1)^{2}+(y0-y1)^{2}+(dx^{2}+dy^{2})t^{2}-2t\sqrt{[(x0-x1)^{2}+(y0-y1)^{2}](dx^{2}+dy^{2})}\frac{(x0-x1)dx+(y0-y1)dy}{\sqrt{[(x0-x1)^{2}+(y0-y1)^{2}](dx^{2}+dy^{2})}} (vt+(r0+r1))2=(x0−x1)2+(y0−y1)2+(dx2+dy2)t2−2t[(x0−x1)2+(y0−y1)2](dx2+dy2) ​[(x0−x1)2+(y0−y1)2](dx2+dy2) ​(x0−x1)dx+(y0−y1)dy​

整理得：
[ v 2 − ( d x 2 + d y 2 ) ] t 2 + 2 ( v ( r 0 + r 1 ) − [ ( x 0 − x 1 ) d x + ( y 0 − y 1 ) d y ] ) t + ( r 0 + r 1 ) 2 − [ ( x 0 − x 1 ) 2 + ( y 0 − y 1 ) 2 ] = 0 [v^{2}-(dx^{2}+dy^{2})]t^{2}+2(v(r0+r1)-[(x0-x1)dx+(y0-y1)dy])t+(r0+r1)^{2}-[(x0-x1)^{2}+(y0-y1)^{2}]=0 [v2−(dx2+dy2)]t2+2(v(r0+r1)−[(x0−x1)dx+(y0−y1)dy])t+(r0+r1)2−[(x0−x1)2+(y0−y1)2]=0
是一个一元二次方程，带入求解公式判断即可。

AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <sstream>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <vector>
#define qcin ios::sync_with_stdio(false)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6+10;
const double eps = 1e-6;
const long long MOD = 1e9+7;



int main()
{
    int t;
    cin >> t;
    double x0, x1, y0, y1, dx, dy, r0, r1, v;
    while(t--)
    {
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf", &x0, &y0, &x1, &y1, &dx, &dy, &r0, &r1, &v);
        double a = v*v - dx*dx -dy*dy;
        double b = 2*(v*(r0+r1) - (x0-x1)*dx - (y0-y1)*dy);
        double c = (r0+r1)*(r0+r1) - (x0-x1)*(x0-x1) - (y0-y1)*(y0-y1);
        double delta = b*b - 4*a*c;
        if(a == 0)
        {
            if(b == 0) puts("Impossible");
            else
            {
                if(-c/b > 0) printf("%.4f\n", -c/b);
                else puts("Impossible");
            }
        }
        else if(delta < 0) puts("Impossible");
        else
        {
            double t1 = (-b - sqrt(delta))/(2*a), t2 = (-b + sqrt(delta))/(2*a);
            if(t1 > t2) swap(t1, t2);
            if(t1 >= 0) printf("%.4f\n", t1);
            else if(t2 >= 0) printf("%.4f\n", t2);
            else puts("Impossible");
        }
    }
    return 0;
}