利用分治策略解决 逆序对计数问题 Counting Inversion Problem
首先来看一下问题详情:


看完题目与例子后,大家对逆序对计数问题有了一个大概的了解,对于这个问题,如果我们用普通的算法即循环嵌套比较能确实能解决,但是不够高效,我们使用分治策略能更有效的解决这个问题,并且在解决这个问题的过程中理解分治、递归等思想。
简单理解分治策略与递归
(这里只简单讲述一下,如果完全没了解过可以看一下:【【算法】分治法归并排序】 )
分治策略的一般步骤:
- 分解原问题:将原问题分解成多个子问题
- 解决子问题:递归的求解各个子问题
- 合并问题解:将结果合并为原问题解
递归思想
这个思想我们可以用一个简单的问题来理解:写一个计算 !n (n 的阶乘)的程序
#include <bits/stdc++.h>
using namespace std;
int method(int n){
if(n==1) return 1;
return n*method(n-1);
}
int main(){
cout<<method(5);
return 0;
}
method()方法就是递归思想的最简单形式
解题开始:
思路:
先来说正常的逆序对计算问题的思想:两个循环嵌套,将第一个元素与第一个元素之后的元素比较大小,然后再用第二元素与第二个元素之后的元素比较大小,问题就解决了
我们利用分治策略解答逆序对计数问题,思路其实就是将长度为 n 的数组分为两个数组,再将两个数组分为 4 个数组,反复操作,直到每个数组中只有一个元素为止,我们就获得了 n 个长度为 1 的子数组,然后将相邻的子数组比较并排序,比较后计数逆序对个数。
代码实现:
我们用文字来解释思路可能大家觉得很简单,但是在代码中利用递归思想来实现还是有一定难度的,以下是我的代码实现并配有详细注释:
//
// Created by ASUS on 2024/10/12._
//
#include <iostream>
#include <vector>
using namespace std;
//利用分治策略解决计算数组中 ---**逆序对计数问题**Counting Inversion Problem_
//归并两个 **有序** 数组,并且计算逆序对
int MergeAndSort(vector<int>& arr,vector<int>& temp,int left,int mid,int right) {
int count = 0;
int i = left; //定义左子数组的起始点_
int k = left; //合并后的数组的起始点_
int j = mid+1; //定义右子数组的起始点_
while( i<=mid && j<=right) {
if(arr[i]<= arr[j]) {
temp[k]=arr[i];_//注意这里k的作用,我们将较小的元素放入我们一开始定义的_**空数组temp**_中_
k++; //k向后移位_
i++; //i向后移位 之后的移位操作不再注释_
}else {
temp[k]=arr[j];
count += (mid-i+1);_//这一步很重要,我们把右子数组中比左子数组中当前元素小的元素个数,加到count中,
//因为此时右子数组中元素比左子数组中当前元素小,所以此时左子数组中当前元素和右子数组中元素构成逆序对
k++;
j++;
}
}
//在上面的while循环中,i<=mid 和 j<=right这两个条件只要有一个不成立循环就会结束,
//换言之就是两个子数组中的元素 **不能全部复制** 到temp数组中去,我们需要把剩下的元素复制到temp数组中,如下操作:_
while(i<=mid) {
temp[k]=arr[i];
k++;
i++;
}
while (j<=right) {
temp[k]=arr[j];
k++;
j++;
}
//到这里,temp数组中是有序数组了,但是之后的操作中我们还是以arr为操作目标,而arr中的顺序 **还是混乱状态**
//我们需要把已经操作过的元素进行排序操作,最简单的方法就是从temp中将元素复制到arr中,如下:_
for(int i=left;i<=right;i++) {
arr[i]=temp[i];
}
//返回我们再排序过程中记录的逆序对个数_
return count ;
}
//利用递归思想拆分数组,并调用MergeAndSort方法计数逆序对个数 注意理解递归思想在这里面的实现_
int MergeCountAndSort(vector<int> &arr,vector<int>& temp,int left,int right) {
int count = 0 ;
//判断递归结束的条件,左右指针重合的时候,即数组中只有一个元素_
if(left<right) {
int mid = (left+right)/2;
//递归操作继续拆分 左部数组,并计算逆序对个数_
//如果能理解这里的调用MergeCountAndSort可以计数逆序对个数,恭喜你,就理解了这里的递归思想了!_
count += MergeCountAndSort(arr,temp,left,mid);
//递归操作继续拆分 右部数组,并计算逆序对个数_
count += MergeCountAndSort(arr,temp,mid+1,right);
//合并两个有序数组,并计算 两个部分_**总的**_逆序对个数_
//这里也是本题中递归的思想的重点 好好想一想这三行代码的执行先后逻辑!_
count += MergeAndSort(arr,temp,left,mid,right);
}
return count;
}
//主函数,也可以没有这一个函数,这是为了main函数中代码的简洁加上的_
int CountInversion(vector<int>& arr) {
//这里定义了我们的目标数组,_
//注意这个数组定义之后只有长度没有值_
vector<int> temp(arr.size());
//调用MergeCountAndSort计算逆序对方法并返回结果_
return MergeCountAndSort(arr,temp,0,arr.size()-1);
}
int main() {
vector<int> arr = {7,5,6,4,9,1,3};
int result = CountInversion(arr);
cout << "数组中的逆序对个数为: " << result << endl;
return 0;
}
例子带入解释:
如果你看了代码之后处于懵懂状态,那我们将{7,5,6,4,9,1,3}这个例子数组带入来理解
这里是文字较多,我尽量加一些逻辑图,做到逻辑清晰,麻烦大家耐心看。
我们通过调用 CountInversion 函数来调用 MergeCountAndSort 这个递归函数(转递的参数大家自己去代码中看),将我们的原数组 arr = {7,5,6,4,9,1,3}转递进去,这里 left=0,right=6,符合 MergeCountAndSort 函数中 if 的判断条件,进入递归。
我们先不管“count +=”,理解这个三行递归思想的代码:
count += MergeCountAndSort(arr,temp,left,mid);
count += MergeCountAndSort(arr,temp,mid+1,right);
count += MergeAndSort(arr,temp,left,mid,right);
这里联系我之前讲递归思想时给的阶乘的例子:我们在定义的 method()函数中再次调用 method 方法,直到 n=1 时才停止递归,通过这样的操作来实现 n*(n-1)*...21 的计算,
而这里我们通过同样的思想来实现分治策略中将问题分为子问题的操作-----通过 1,2 行代码再调用 MergeCountAndSort 方法,但是注意传递给函数的参数改变了;第一行代码中”(arr,temp,left,mid)“,把 mid 索引作为第一次拆分数组中,左数组的结束索引(结合我画的图来看),第二行代码中”(arr,temp,mid+1,right)“,把 mid+1 作为第一次拆分数组中,右数组的开始索引;然后再在调用的 MergeCountAndSort 再次调用 MergeCountAndSort 函数第二次拆分,反复操作直到得到所有的子数组。
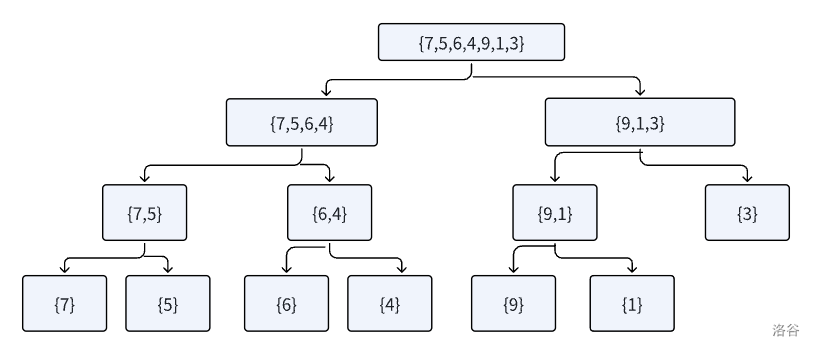
这里有一个很重要的点!!!我画出来的数组是为了方便大家理解,在程序的运行中实际上并没有这些子数组存在,从始至终都只有 arr 和 temp 这两个数组,子数组在我们脑海中的出现只是因为我们对起始索引和结束索引的值的改变来达到拆分数组的效果!!!!!!!
这个点可以很好的解释 MergeAndSort 中的操作,大家想不明白 MergeAndSort 函数中的代码时,可以好好想想 left 和 rigth 变量不同数组中是什么值,你就会明白了
**好好想一想这三行代码的执行先后逻辑! **我的代码注释中这样写的,我们解释一下:
提问:你能想出这这些拆分出的数组的出现先后顺序吗?
三行代码中第一行毫无疑问第一个运行,但是由于递归操作,函数再调用函数本身,导致第一行调用 MergeCountAndSort 函数之后,第一个出现的是 {7,5,6,4},代码执行还在第一行代码内,没有轮到第二行代码,故第二个出现的数组并不是 {9,1,3},第一行代码的执行中再次调用函数,出现了 {7,5},再调用出现 {7},返回上一次调用函数的第二行代码出现{5},再返回上一次调用函数的第二行代码出现{6,4},然后才依次是{6},{4}, {9,1,3}, {9,1}, {9}, {1}, {3} (这个顺序倒是和二叉树的某种遍历方式暗合哈哈)
再次强调实际上并没有这些数组存在,从始至终都只有 arr 和 temp 这两个数组
如果你把上一段描述看明白了的话,就应该知道第一次调用 MergeAndSort 函数是什么时候了
没错,就是在{5}这个数组出现之后,那一次调用函数方法第一次来到了第三行代码----对两个子数组{7}和{5}进行排序与计数逆序对,然后操作的是{6},{4}两个子数组,经这两次操作之后, {7,5}{6,4}这两个数组其实变成了{5,7}{4,6}(这里想不明白的话反复思考我说的子数组实际不存在这个事实)。
然后在反复的操作中,我们的count=1+1+3+1+1+8=15 (我给的数字的顺序就是 count 从 0 变成 15 的顺序,可以带入例子自己思考一下是不是这样的)
结束
希望能帮助到大家理解分治策略和递归的思想,我也是一个算法小白,自己解决了这个问题之后把思路记录了下来,如果代码或讲解有误的话欢迎大家提出来哦!谢谢大家的观看!!!




 京公网安备 11010502036488号
京公网安备 11010502036488号