搜索算法

前言-INTRODUCTION

简单来讲，任何可以看成图的数据集合在查找和统计中，都会用到搜索，也就是查找特定数据，这是一个非常朴素的概念， 就像统计班上有多少玩 暗区突围 的人一样，去查找，并统计。

当然，搜索总是用在图论上。

假如搜索有固定方式，那么搜索可以分为两种，也就是 深度优先搜索 和 广度优先搜索 。

一、BFS 和 DFS 的理解-THE DEFINITION OF BFS AND DFS：

DFS :全称 深度优先搜索 （Depth First Search），简称 深搜 ，其原理简述为对每一个可能的分支路径深入到不能再深入时停下，回溯并对其他分支路径再次深入，直到无分支路径可走为止。

BFS :全称 广度优先搜索 （Breadth First Search)，简称 广搜 ，其原理简述为系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

以走迷宫为例，

我们的一种策略是，在分叉路口随便选一条路走下去，一直如此，如果最后没路，就回到上一个岔路口选另一条路走，直到目的地，或者在回到上一岔路口时发现回到了起点，说明无法走出迷宫。

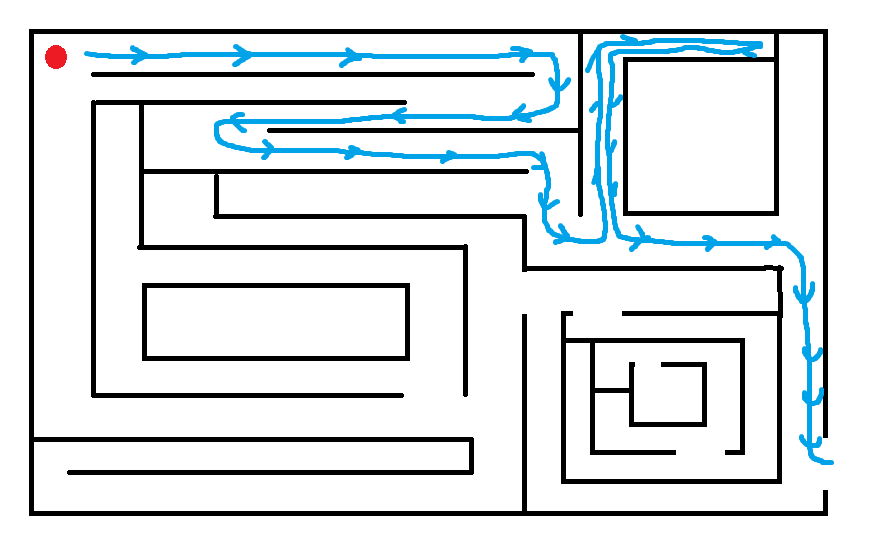
另一种策略是，记录每种可能，并同时走每条路，找到终点。

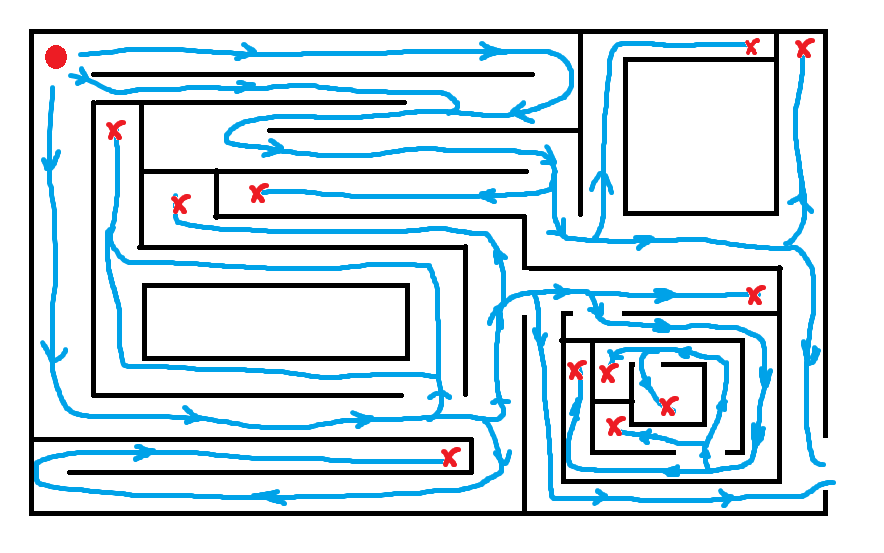
其实我们总是会选择第一种策略，这是因为DFS在一定概率下更快，所需的记忆空间更少，并且走迷宫的目的不是找出最短路，而是走出去。

那么在导航系统中，忽略路况时间限行等问题时，用的是BFS，毕竟要找到最短的路径。

由上我们可以简单的比较一下深搜和广搜，

算法	空间复杂度	时间复杂度	代码实现难度	搜索效率
DFS		~	较低	不稳定，可快可慢
BFS			较高	稳定，较慢

其实，深搜的局限性还是很大的，因为无论是找路径数量还是找最短路，深搜总是慢于广搜；且在越来越难的题中，递归的使用将更有限，后面将说到“深搜即递归”；其次，在后面，更多的算法都是基于广搜。

二、BFS & DFS 的代码实现-THE PRACTICE OF BFS AND DFS:

由于深搜总是相对于每一个点来遍历，所以深搜的主体采用了递归的方式： 对于当前每一个点来讲，是否继续向下遍历，是否回溯，是否剪枝……

当然，有遍历就有可能会重复遍历，所以还要加上一个标记。

bool ……;//标记是否遍历过 

void dfs(int u){//总是需要记录一下当前步数 
	if(__){//判断 是否到达终点 或 达到指定步数 
		……//操作
		return ;//回溯 
	} 
	for(……){//遍历相连的点 
		if(__) {//看是否遍历过 
			……;//先标记
			……;dfs(……);……;//后操作
			……;//最后复原 
		} 
	} 
}

在做题的过程中，深搜的代码样式由题目性质决定，什么时候深搜？如何深搜？有没有必要再搜？通过这些问题来编写最优代码是极好的，因为这就是普遍意义上的剪枝。

那么广搜要复杂一点，因为广搜就像是水波在水面荡漾，一圈一圈向外扩张，所以广搜是一层一层的，我们可以用一队列来储存即将遍历的一层点，遍历操作完后就弹出，这时对于每一个点来讲操作又是相同的，但还有下一层要遍历，所以广搜用递归的话每次递归时对于上下队列的处理繁琐，较复杂，不易使用，那就只用一个队列，这个队列不断弹出上一层遍历过的点，又不断加入下一层要遍历的点。

假如你学过图论最短路，那么你会发现这 BFS 与 算法十分类似，尤其是堆优化的 算法，并且，可以发现，对于到起点的距离来讲，BFS 的队列是永久单调递增且分为两段的，此时 BFS 与 相互证明了正确性。

bool ……;//标记是否遍历过
 
struct kkk{
	……; 
}queue[N];//遍历队列，这里用手打队列
int hh=0,tt=0;//头指针，尾指针 

void queueinit(){
	……;//初始化使指针可以正常运行 
}
//注意，这里的指针运用与常规使用不同，所以不要混淆 

void bfs(int u){//记录一下当前步数，也可以无输入 
	while(hh!=tt){//队列不空 
		//当前操作队头 
		if(……){//判断是否遍历过 
			……;hh++;//操作,要队头弹出 
			continue; 
		}
		……;//操作
		……;tt++;……;//更新队列
		hh++;//队头弹出 
	}
}

可以看出宽搜的主体就是一个循环。

假如想使用 ：

struct node{
	…… 
};

… st …; 

void bfs(……){
	queue<node> q;
	memset(st,…,sizeof st);
	//init
	q.push( …);
	st …= …;
	
	while(!q.empty()){
		node u=q.front();
		q.pop();
		for(……){
			……;
			if( …){
				q.push( …);
				…… 
			}
		}
	}
	
	…… 
}

三、DFS 的优化剪枝-THE IMPROVEMENT OF THE DFS

上面提到在编写 DFS 代码时代码样式往往由题目性质决定，剪枝就是对 DFS 的优化，那么有五种常见的优化方式：

• 优化搜索顺序

一般情况下，应当 。

我们知道，DFS 是以递归的形式呈现的，那么这就涉及到爆栈的问题，优先搜索分支节点少的节点可能更快的得到。

什么意思呢？

拿luogu P10483 小猫爬山来讲，我们的搜索或枚举方式是，以深搜的方式遍历每只小猫，对于每只小猫可以合理放到已有的任意缆车中，或者新开一辆缆车。

其优化方式在于，对于质量轻的小猫来讲，它能够放到的缆车多，即深搜分支节点多，而质量重的小猫的选择更少，即分支节点少，所以，这里我们优先从重的小猫开始搜索，即降序搜索。

可别小看了这点优化，即使是上面的例题，时间可以优化到 ，这是对比：排序深搜与普通深搜。

• 排除等效冗余

应当 。

以luogu P1120 小木棍为例。

我们的搜索策略与luogu P10483 小猫爬山类似，即以分组的形式来还原最初的木棍，这中间还可以加一个可行性剪枝——每一组的长度必须为总长度的约数，否则得不到整数个组；

其次，与小猫爬山类似，我们从较大的木棍开始尝试组合；

然后，由于此时长度相同的木棍较多，所以对于两个长度相同的木棍来讲，没有必要都枚举一遍，所以我们需要设置一个转跳点，直接到达下一个不同长度的木棍;

接着，可以发现，在每一组木棍内部，任意木棍交换顺序是等效的，这意味着如果当前枚举的木棍之后枚举失败，那就没有必要再往后枚举，不应跳过当前木棍深入，应当回溯。

• 可行性剪枝

。

• 最优性剪枝

。

• 记忆化搜索（DP）

字面意思。

• 状态压缩

以二进制压缩为例，

另提一嘴，二进制压缩在 DP 里面还是应用广泛的，然而有的时候我们能感受到，深搜与 DP 本质上是变形的枚举。

回归正题，以luogu P1784 数独为例，

我们的搜索策略是，每一次深入选择可能填数最少的空格开始搜索，并且可行性剪枝。然而难点在于如何判断可行性，此时就用上二进制压缩，我们把每行每列每个九宫格的未填数字压缩到一个整数里，这个整数的第几位为 几就可以被填入，那么对于一个格子来讲，将他的列状态、行状态与宫格状态 & 起来，即可判得可放那些数。

这是笔者的样例代码：luogu P1784 数独 题解 。

• 总结与练习-CONCLUSION AND EXERCISE

从玄学剪枝到理论深搜

四、迭代加深——DFS 的回首-ITERATIVE DEEPENING SEARCHING : DFS'S HEAD BACK

前面我们讲过，对于朴素的 DFS 搜索方式，是有一定局限性，当答案位于搜索树较浅的一层而搜索过程中到了更深的非解道路时，这是费时费力的，并不高效。

然而迭代加深是指自发的限制一个搜索范围，或说深度，在这一范围内以深搜的形式搜索，如果最终未得到解，则扩大搜索范围。

迭代加深是对 DFS 的一种改进，显然他不适用于 BFS 。

那么，当答案在最深处时，迭代加深的时间复杂度是否很高呢？以二叉树为例，在第 层应有 个节点，其之前的节点有 个节点，就算再怎么搜，时间复杂度只会接近 ，那么对于多叉树来讲，时间复杂度必小于 。

但说老实话，DFS 基本只用于简单题，一般到不了用迭代加深的地步，而难题一般都用 BFS 或 算法。

五、拓扑序列—— BFS 的应用-TOPOLOGICAL ORDER FOR THE USE OF BSF

• 1.拓扑序的定义-THE DEFINITION OF THE TOPOLOGICAL ORDER

拓扑次序( )的序列，简称拓扑序列，是一种线性序列，只存在于有向图中。

若一个由图中所有点构成的序列 满足：对于图中的每条边 ， 在 中都出现在 之前，则称 是该图的一个拓扑序列。

由定义可知，若一个有向图存在环，则此图一定不存在拓扑序列；反之亦然，若一个图存在拓扑序列，则此图一定不存在环。同时可以证明，一个有向无环图一定存在拓扑序列，因此，有向无环图也被称为拓扑图。

• 2.拓扑序的求解-SOLOVING TOPOLOGICAL ORDER

显然，凡是涉及拓扑序列，总是会想到如何求一个有向图的拓扑序列。

我们发现，在拓扑序列中，对于一个非头非尾的点 来讲， 之后的节点 一定不存在有边由 指向 ， 之前的节点 一定不存在边由 指向 。

那么，对于第一个点 来讲，没有任何点有边指向 ， 之前没有任何起点， 一定不为任何起点；对于最后一个点 来讲， 不指向任何边，且 只作为终点，不是任何边的起点。

翻译一下，就是拓扑序列的第一个点一定是入度为 的点，最后一个点一定是出度为 的点。（度数：图论芝士）。

结合BFS，是否有点想法？从一个入度为 的点开始，到一个出度为 的点结束，我们的策略是：

显然，所有入度为0的点都是可以作为起点的，因为没有任何一条边指向它，即没有任何一个点能在它的前面,所以我们先让所有入度为0的点入队，此时剩下的节点一定就为入度不为0的节点了。

你看，所有入度为0的点都已经放在前面了，假设其中有个节点A，有条边由A指向B，那意思是不是说，B一定在A的后面？答案是肯定的，这样我们就保证了节点A的所有出边所连的节点都是一定满足以上规律的，

既然这样，这些边对于A便没有任何作用了，我们将这些边删掉。删掉后，如果B也变成了入度为0的点，那又可以将B放入队列，以此类推。

例题：B3644

代码：

#include<iostream>
#include<cstring>
using namespace std;
const int N=110;
int n;
int h[N],e[N*N],ne[N*N],ids;//领接表 
int d[N];//度数
int q[N],hh=0,tt=-1;
 
void add(int a,int b);

void tpsort(){
	for(int i=1;i<=n;i++)
		if(!d[i])
			q[++tt]=i;
	while(hh<=tt){
		int t=q[hh++];
		for(int i=h[t];i>=0;i=ne[i]){
			int j=e[i];
			d[j]--;
			if(!d[j])	q[++tt]=j;
		}
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin>>n;
	memset(h,-1,sizeof h);
	for(int i=1;i<=n;i++){
		int v;
		cin>>v;
		while(v!=0){
			add(i,v);
			d[v]++;
			cin>>v;
		}
	}
	tpsort();
	for(int i=0;i<=tt;i++)
		cout<<q[i]<<' ';
	return 0;
} 

void add(int a,int b){
	e[ids]=b;
	ne[ids]=h[a];
	h[a]=ids++;
}

六、BFS 的应用模型-THE APPLICATION MODEL OF BSF:

• 回顾-REVIEW

可以发现 BFS 的以下特征：

1. 趋向于“求最小”问题
2. 基于迭代（非递归，不会爆栈）

在深度剧大、节点较多的情况下我们会更倾向于用 BFS。

• 模型1 Flood Fill

如其名，就像洪水填充一样，在最开始的点“注入水”（标记），然后在点能到达的地方“注入水”，直到再也无法“覆盖”更多的点。

当然，这样一种模型不仅可以用 BFS 实现，DFS 也是可以的，但有爆栈的风险，一般用 BFS 。

这样一个用 BFS 实现的模型可以在线性时间复杂度内，找到某个点所在的连通块。

这样看来，此模型相当简单 只恨码力不足 ，但很常见。

• 例题-Example for Flood Fill

• luogu P1331 海战

• luogu P1457 [USACO2.1] 城堡 The Castle ：结构体，特殊性质判断与应用，二进制压缩

• 模型2-Solving the shortest path

BFS 确实与图论有着不可忽视的孽缘，然而，BFS 实际只能解决的边权为 或相同的图的最短路问题。

要求出最短距离很简单，然而假如我们想求出任意一条最短路径时，对于 BFS 来讲这有一点麻烦，

如何求最短路径？ 为了方便，我们把 st 数组改为 node 类型，并一般使用负数来表示未走过，走过时用从哪里走来的那个点来标记 st ，这样我们能通过 st 反向推得路径，为了方便，我们需要从终点开始 BFS ，然后从起点反向推路径。于是上述的 st 就变为 pre 。

如何更新 pre呢？ 取第一次到达的“来时路”，显然，对于一个从队列里拿出来的新节点 a ，当更新到其指向节点 b 时，此时队列里的其余节点到起点的距离大于等于 a 到起点的距离，那么假若 b 在最短路径中，就必然有一条路径通过 a 、 b ，那怕有与 a “同层”（到起点相同）的点可通往 b ， a 、 b 这条路径也一定是一条解。

• 例题-Example for solving the shortest path

• luogu P1746 离开中山路

• 模型3-The least steps

例如luogu P1379 八数码难题这样以全局状态为起点和终点的题，称其为“最小步数”问题类型，考虑自定义状态压缩和 unoredered_map 或 map 的使用。

以例题为例：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int g[3][3];
unordered_map<string,int> dis;

void setn(string x){
	int z=0;
	for(int i=0;i<3;i++){
		for(int j=0;j<3;j++){
			g[i][j]=int(x[z++]-'0');
		}
	}
}

string getn(){
	string res;
	for(int i=0;i<3;i++){
		for(int j=0;j<3;j++){
			res+=char(g[i][j]+'0');
		}
	}
	return res;
}

string moven(string x,int v){
	setn(x);
	int x0,y0;
	for(int i=0;i<3;i++)
		for(int j=0;j<3;j++)
			if(g[i][j]==0){
				x0=i,y0=j;
				break;
			}
	int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};
	if(x0+dx[v]>=0 && x0+dx[v]<=2 && y0+dy[v]>=0 && y0+dy[v]<=2){
		int gh=g[x0][y0];
		g[x0][y0]=g[x0+dx[v]][y0+dy[v]];
		g[x0+dx[v]][y0+dy[v]]=gh;
	}
	return getn();
}

void bfs(string st,string ed){
	if(st==ed)	return ;
	queue<string> q;
	q.push(st);
	dis[st]=0;
	while(q.size()){
		string u=q.front();
		q.pop();
		
		string uto[5];
		for(int i=0;i<4;i++)
			uto[i]+=moven(u,i);
		
		for(int i=0;i<4;i++){
			if(dis.count(uto[i])==0){
				dis[uto[i]]=dis[u]+1;
				if(uto[i]==ed)	return ;
				q.push(uto[i]);
			}
		}
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	string st,ed;
	cin>>st;
	ed="123804765";
	bfs(st,ed);
	cout<<dis[ed]<<endl;
	return 0;
}

变态者要求求其路径，此时参考模型2。

七、多源BFS·超级原点思想-MULTISOURCE BFS ·THE THOUGHT OF SUPER ORIGINAL POINT

以例题为例：AcWing 173.矩阵距离

我们反过来想，假设有一个超级原点与所有的 1 相连且边权为 ，于是我们求超级原点到任意 0 的最短路，并储存到对应位置上，即得答案。

八、双端队列BFS-DEQUE BFS

当遇到边权只有 或 的图时，可以使用双端队列BFS来求解最短路，例如：AcWing 175.电路维修。

有点类似与动态规划的图论理解。

对于双端队列的用法为，在更新节点 到其所连接节点 时，若当前边权为 时，插入队头；若为 ，则插入队尾。

九、双向搜索-MEET IN THE MIDDLE

双向广搜-two-way BFS

显然，同时从起点和终点开始广搜可以大大减少加入到队列中的状态或节点，于是可以达到大于等于 的优化率。

然而，双向广搜也是有使用范围限制的，综合考虑实用性，双向广搜的代码十分复杂（相对普通广搜来讲），难以实现；然而当数据范围十分大时，就只能用双向广搜来优化。

当然，双向广搜还可以优化，为了平衡两头的搜索规模，每次扩展总是选队列长度较小的一方来扩展，这样有几率大大优化。

例如例题：luogu P1032 字串变换

代码样例：

#include<bits/stdc++.h>
using namespace std;
const int N = 10;
string a,b;
string x[N],y[N];
int n;
typedef unordered_map<string,int> unmapsi;

int extend(queue<string> &q,unmapsi &sst,unmapsi &sed,string sa[],string sb[]){
	//注意，这里引用了扩展队列，两个标记数组这样方便
	//在本题中，显然字串的变换是由方向性的，所以从起点开始和从终点开始规则不一样 
    string u=q.front();
    q.pop();
    for(int i=1;i<n;i++){
        for(int j=0;j<u.length();j++){
            if(u.substr(j,sa[i].length())==sa[i]){
                string got=u.substr(0,j)+sb[i]+u.substr(j+sa[i].length());
                if(sed.count(got))   return sed[got]+1+sst[u];
				//在“终点”里找到当前转移点 
                if(sst.count(got))   continue;
                //已经在更短的距离下到达这个点，无需加入 
                sst[got]=sst[u]+1;
                q.emplace(got);
            }
        }
    }
    return 25;//扩展结束 
}

int bfs(){
    queue<string> st,ed;//双向搜索的两个队列 
    unmapsi sst,sed;//两个队列分别对应的标记，用的unordered_map 
    st.emplace(a,0);
    ed.emplace(b,0);
    sst[a]=0;sed[b]=0;//init 

    while(!st.empty() && !ed.empty()) {
        int t; 
        if(st.size()<=ed.size()) t=extend(st,sst,sed,x,y);//折半优化 
        else    t=extend(ed,sed,sst,y,x);
        if(t<=10)   return t;
    }

    return 34;//无答案 
}


int main(){
    cin>>a>>b;
    n=1;
    while(cin>>x[n]>>y[n])  n++;//无限制输入 
	
    int step=bfs();
    if(step>10) puts("NO ANSWER!");
    else printf("%d\n",step);
    return 0;
}

双向深搜-two-way DFS

例题：luogu P4799 [CEOI2015 Day2] 世界冰球锦标赛

由于深搜的特殊方式，即一直搜而少回头，所以双向深搜往往需要将“搜索树”（非 ,指的是搜索时的状态转移形成的似树结构）分成两半，每一半分开搜索，来减少时间复杂度。

例如例题的枚举，实际上最多要枚举 状态，但实际上当枚举到 状态时，就已经有很多情况不符合条件了，由此我们把这里的枚举分成两个用相同方法枚举的部分，一个部分枚举 大约 级别的样子，

同时在合并时，显然当我们知道其中一部分的花费时，另一部分的花费就有了一个最大值，而所有比这个最大值小的方案都可以，所以我们使用排序与二分。

这样总体下来时间复杂度为 。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e8;
int n;
ll m;
ll w[50];

ll f[N],s[N];
int cntf,cnts;

void dfs(int l,int r,ll val,ll sum[],int &cnt){
	if(val>m)	return ;
	if(l>r){
		sum[++cnt]=val;
		return ;
	}
	dfs(l+1,r,val+w[l],sum,cnt);
	dfs(l+1,r,val,sum,cnt);
}

int main(){
	scanf("%d%lld",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%lld",&w[i]);
	int mid=n/2;
	dfs(1,mid,(ll)0,f,cntf);
	dfs(mid+1,n,(ll)0,s,cnts);
	sort(f+1,f+cntf+1);
	sort(s+1,s+cnts+1);
	ll ans=0;
	for(int i=1;i<=cnts;i++)
		ans+=upper_bound(f+1,f+cntf+1,m-s[i])-f-1;
	printf("%lld",ans);
	return 0;
}

十、最后的神明·A*-THE LAST GOD:A*

在一开始，不同的搜索方式影响了搜索效率，即DFS、BFS；后来随着搜索规模的增大，我们想到了双向搜索；当搜索规模继续扩大时，这时我们便需要用到搜索里面最强大的搜索方式—— 。

简单来讲，带有估价函数（又称启发函数）的优先队列 BFS 就称为 算法。

从字面意思上来讲，估价函数就是对当前状态到目标状态的距离的估计范式，而此时优先队列 BFS 的队列存各个状态到起始状态的距离和到目标状态的估计距离之和，并以此优先排序。

看起来，与 算法很像，我们甚至可以说 就是所有状态的估价函数为 的 算法。

算法的核心便是估价函数，而估价函数应当满足估计值小于等于实际值且大于等于，否则 不成立。

证明：反证法——设取出一个节点且通过此节点的路径长度 大于最优解 ，由估价函数估计值小于等于实际值的性质可知，对于得到最优路径时取出的节点 来讲，其得到的路径长度（到起点的实际距离和估价函数之和） 满足 ，则可知 ，这显然违背优先队列的性质。得证。

估价函数的估值与实际值越接近， 算法的效率显然越高。

注意， 一般用于搜索空间巨大的情况，倘若空间过小，还不一定为最优解。

以例题luogu P2901 [USACO08MAR] Cow Jogging G为例：

此时我们将提到 的另一个性质：当终点第几次在队列中被取出，即得第几短路的距离。

证法与上述证明类似。

这里直接将每个点到终点的距离当做估价函数。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;//注意数据范围 
const int N = 1010,M = 1e5;
#define x first
#define y second
typedef pair<ll,ll> PII;
typedef pair<ll,PII> PIII;

int h[N],rh[N],ed[M],ne[M];
ll len[M];
int idx;
void add(int he[],int st,int fi,ll le){
	ed[idx]=fi,ne[idx]=he[st],len[idx]=le,he[st]=idx++;
}

int n,m,k,a,b;

ll dis[N];
bool s[N];


void dijistra(){
	priority_queue<PII,vector<PII>,greater<PII> > q;
	memset(dis,0x3f,sizeof dis);
	dis[b]=0;
	q.push({0,b});
	while(!q.empty()){
		PII u=q.top();
		q.pop();
		
		if(s[u.y])	continue;
		s[u.y]=true;
		
		for(int i=rh[u.y];~i;i=ne[i]){
			int v=ed[i];
			if(dis[v]>dis[u.y]+len[i]){
				dis[v]=dis[u.y]+len[i];
				q.push({dis[v],v});
			}
		}
	}
}

int astar(){
	priority_queue<PIII,vector<PIII>,greater<PIII> > q;
	q.push({dis[a],{0,a}});
	
	int cnt=k;
	while(q.size()){
		PIII u=q.top();//按估值取点 
		q.pop();

		if(u.y.y==b)	cnt--,printf("%lld\n",u.y.x);	
		if(cnt==0)	return 0;
		
		for(int i=h[u.y.y];~i;i=ne[i]){
			int j=ed[i];
			q.push({u.y.x+len[i]+dis[j],{u.y.x+len[i],j}});//疯狂入队 
		}
	}
	
	return cnt;
}

int main(){
	memset(h,-1,sizeof h);//图初始化 
	memset(rh,-1,sizeof rh);//反向图初始化 
	scanf("%d%d%d",&n,&m,&k);
	a=n,b=1;
	for(int i=1;i<=m;i++){
		int u,v;
        ll l;
		scanf("%d%d%lld",&u,&v,&l);
		add(h,u,v,l);//建边 
		add(rh,v,u,l);//反向建边 
	}
	dijistra();//估价函数初始化 
	int t=astar();//A*
	while(t--)	printf("-1\n"); 
	return 0;
}

显然，这里并没有详细说明如何构造估价函数，但这正是 算法的难点。

带有估价函数的迭代加深 DFS 算法就是 。

关于 算法：，跟 DFS 类似的是，能用 不用 。当然特殊情况下只能用 而不能用 ,例如当状态极其庞大以至于队列难以容纳的情况，并且 一般也比 好写。

当你的状态十分难以维护并且搜索深度相对较深，而且答案还比较浅时，那就用 。

以 UVA 1343 旋转游戏 The Rotation Game 为例：

当然，需要使用迭代加深，那么如何维护一个如此复杂的结构呢？答案是自定义加打表，如代码所示。

那么这里的估价函数，我们期望，初时情况下中间八个格子中数量最多的数字 便是最终时的数字，那么在无视合法操作的情况下，我们至少需要 次操作（换一个数为一次操作，因为按照合法操作，一次操作后八个格子中必变一个数，当然这个数不一定是我们想要的），于是，就把这个当做估价函数。

最后有一点排除等效冗余，即操作一次 A 后不该操作 Z 。

#include<bits/stdc++.h>
using namespace std;
struct code{
	int sp[24];
};
code in;
int ans[10010000];
int ans2=114514;

bool same(int a,int b){//等效冗余判断打表
	if(a>b)	swap(a,b);
	if(a==1 && b==6)	return true;
	if(a==2 && b==5)	return true;
	if(a==3 && b==8)	return true;
	if(a==4 && b==7)	return true;
	return false;
}

int chor[8]={6,7,8,11,12,15,16,17};

int check(code x){//得到估价函数
	int s[4]={0};
	bool flag=true;
	for(int i=0;i<8;i++){
		s[x.sp[chor[i]]]++;
		if(i<7 && x.sp[chor[i]]!=x.sp[chor[i+1]])
			flag=false;
	}
	if(flag)	return 0;//八个格子数字相同
	else{
		int nu=-1;
		for(int i=1;i<4;i++)
			if(nu<s[i])	nu=s[i];
		return 8-nu;
	}
}

char couten(int x){//打表
	if(x==1)	return 'A';
	if(x==2)	return 'B';
	if(x==3)	return 'C';
	if(x==4)	return 'D';
	if(x==5)	return 'E';
	if(x==6)	return 'F';
	if(x==7)	return 'G';
	if(x==8)	return 'H';
}

int moor[8][7]={{0,2,6,11,15,20,22},
			   {1,3,8,12,17,21,23},
			   {10,9,8,7,6,5,4},
			   {19,18,17,16,15,14,13},
			   {23,21,17,12,8,3,1},
			   {22,20,15,11,6,2,0},
			   {13,14,15,16,17,18,19},
			   {4,5,6,7,8,9,10}};//打表

void modify(code &x,int g){
	g--;
	int h=x.sp[moor[g][0]];
	for(int i=0;i<6;i++)
		x.sp[moor[g][i]]=x.sp[moor[g][i+1]];
	x.sp[moor[g][6]]=h;
}

bool dfs(int u,int depth,code a){
	int cc=check(a);
	if(!cc){//发现答案
		ans2=a.sp[6];
		return true;
	}
	if(u && cc+u>depth)	return false;//估价函数剪枝
	if(u>depth)	return false;//迭代加深边界
	
	for(int i=1;i<=8;i++){
		if(!u || !same(i,ans[u-1])){//排除等效冗余
			code b=a;
			modify(b,i);
			ans[u]=i;
			if(dfs(u+1,depth,b))	return true;
		}
	}
	
	return false;
}

int main(){
	while(1){
		scanf("%d",&in.sp[0]);
		if(in.sp[0]==0)	break;
		for(int i=1;i<24;i++)
			scanf("%d",&in.sp[i]);
		if(!check(in))	printf("No moves needed\n%d\n",in.sp[6]);//无需操作
		else{
			int depth=1;
			while(!dfs(0,depth,in))	depth++;//迭代加深
			for(int i=0;i<depth;i++)
				printf("%c",couten(ans[i]));
			puts("");
			printf("%d\n",ans2);
		}
	}
	return 0;
}