问题描述：每次可以爬1个或2个台阶，问爬到第 n 个台阶，一共有多少种不同的方法？

方法一：斐波那契数列；

方法二：动态规划O(n)；

方法三：

可以利用矩阵乘法的特性将时间复杂度优化到O(logN)。
在线性代数中，斐波那契数列通项公式被表述成以下形式：

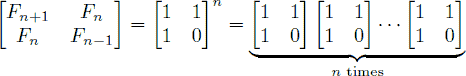
优化：快速地求矩阵的n次方
（1）利用二分的思想：假设要求矩阵的n次方为A(n)，设i=n/2，若n%2==1，则 A(n)=A(i)*A(i)*A(1)，若n%2==0，则A(n)=A(i)*A(i)；
（2）利用二进制思想：将N拆为二进制数，譬如13=(1101)2，那么 A^13= A^8 * A^4 * A^1。这个方法在求快速幂模的时候经常用。

方法四：