离散化树状数组求逆序对

离散化树状数组求逆序对

今天在学校 $oj$oj上看见一道求逆序对的题，上一次企图用冒泡排序做，结果wa了几发。学习树状数组时，猛然发现树状数组还可以求逆序对，于是打开了新的大门。
传送门：39.106.31.26/problem.php?id=3677（洛谷也有这道题P1908）

猫猫TOM和小老鼠JERRY最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。最近，TOM老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中 $a_i\&lt;a_j$ai​<aj​且 $i\&lt;j$i<j的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。
$Input$Input
$第一行，一个数n，表示序列中有n个数。（n\le 40000)$第一行，一个数n，表示序列中有n个数。（n≤40000)
$第二行n个数，表示给定的序列。$第二行n个数，表示给定的序列。
$Output$Output
$给定序列中逆序对的数目。$给定序列中逆序对的数目。
$Sample$Sample $Input$Input
6
5 4 2 6 3 1
$Sample$Sample $Output$Output
11

解题思路

我们针对样例来理解如何采用树状数组求逆序对。

1：

最初的条件如下：

2：

我们利用update(5)，将第5个位置置为1。计算 $[1,5]$[1,5]上比5小的数字，这里用到了树状数组的 $getsum\left(x\right)$getsum(x)操作，现在用输入的下标 $i-getsum\left(x\right)$i−getsum(x) 就可以得到对于逆序数。即： $getsum\left(5\right)=1,res=i-getsum\left(5\right)=1-1=0。$getsum(5)=1,res=i−getsum(5)=1−1=0。

update函数：
void update(ll x){
	while(x<=n){
		ans[x]++;
		x+=lowbit(x);
	}
}

getsum函数：
ll getsum(ll x){
	ll res=0;
	while(x){
		res+=ans[x];
		x-=lowbit(x);
	}
	return res;
}

3：

跟上面情况相同，先把第4个位置置为1， $getsum\left(4\right)=1,res=i-gesum\left(4\right)=2-1=1$getsum(4)=1,res=i−gesum(4)=2−1=1

4：

把第2个位置置为1， $getsum\left(2\right)=1,res=i-gesum\left(2\right)=3-1=2。$getsum(2)=1,res=i−gesum(2)=3−1=2。

5：

把第6个位置置为1， $getsum\left(6\right)=4,res=i-gesum\left(6\right)=4-4=0。$getsum(6)=4,res=i−gesum(6)=4−4=0。

6：

把第3个位置置为1， $getsum\left(3\right)=2,res=i-gesum\left(3\right)=5-2=3。$getsum(3)=2,res=i−gesum(3)=5−2=3。

6：把第1个位置置为1， $getsum\left(1\right)=1,res=i-gesum\left(1\right)=6-1=5。$getsum(1)=1,res=i−gesum(1)=6−1=5。

7：

把每一步的res加起来就是最后的答案了， $sum=0+1+2+0+3+5=11。$sum=0+1+2+0+3+5=11。

这道题看似仿佛已经讲完了，但是仔细思考思考里面居然有一个大坑。这个坑是我们树状数组造成的。当我们输入的值 $a_i=999999999$ai​=999999999这样庞大的值是，数组 $ans\left[x\right]$ans[x]是肯定存不下的。取一个极端情况，有两个值： $a_1=1,a_2=10^{10}$a1​=1,a2​=1010,按照上面的要求我们需要使 $ans\left[10^{10}\right]=1$ans[1010]=1,那么这个数组大部分内存都浪费了，并且也不支持你开这么大，在这样的情况下，我们将数组离散化。

推荐一篇写离散化的blog：
https://blog.csdn.net/qq_41754350/article/details/81199993

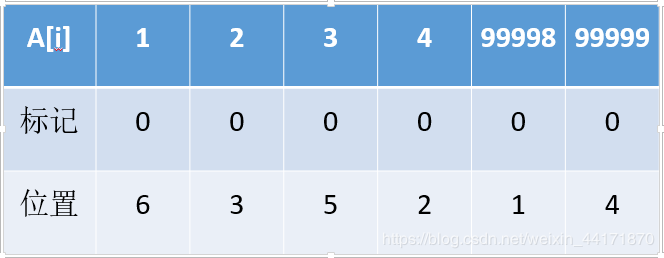
简单的说就是我们用数值下标替代了它的值进行操作。

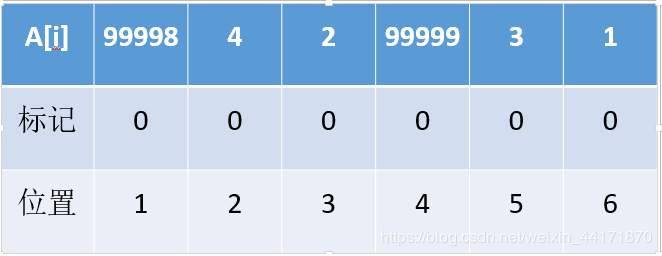
将上述的 $A\left[i\right]$A[i]进行排序，用位置 $b\left[i\right]$b[i]代替自己的原来的值，起到离散化作用。

没想到吧，这里居然还有个坑，离散化的数据一定要去重，不然在求逆序数时会得到错误的解。为了能够偷懒，给大家推荐一个排序：stable_sort()用法和sort()差不多，好处是能去重嘛，要是不懂大家可以百度一下。

最后上代码：

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll maxn=5*1e5+10;
ll b[maxn],n,ans[maxn];
struct code{
	ll val,wz;
}a[maxn];
bool cmp(code a,code b)
{
	return a.val<b.val;
}
ll lowbit(ll x){
	return x&(-x); 
}
void update(ll x){
	while(x<=n){
		ans[x]++;
		x+=lowbit(x);
	}
}
ll sum(ll x){
	ll res=0;
	while(x){
		res+=ans[x];
		x-=lowbit(x);
	}
	return res;
}
int main(){
	ll res=0,i;
	scanf("%lld",&n);
	for(i=1;i<=n;i++){
		scanf("%lld",&a[i].val);
		a[i].wz=i;
	}
	stable_sort(a+1,a+1+n,cmp);//稳定排序 
	for(i=1;i<=n;i++){
		b[i]=a[i].wz;//离散化
	}
	for(i=1;i<=n;i++){
		update(b[i]);
		res+=i-sum(b[i]);
	}
	printf("%lld\n",res);
}