- 基础知识: 常见的BFS用来解决什么问题?
(1)简单图(有向无向皆可)的最短路径长度,注意是长度而不是具体的路径
(2)拓扑排序
(3) 遍历一个图(或者树)
- BFS基本模板(需要记录层数或者不需要记录层数)
- 多数情况下时间复杂度空间复杂度都是O(N+M),N为节点个数,M为边的个数
- 基于树的BFS:不需要专门一个set来记录访问过的节点
Leetcode 102 Binary Tree Level Order Traversal
Leetcode 103 Binary Tree Zigzag Level Order Traversal
Leetcode 297 Serialize and Deserialize Binary Tree (很好的BFS和双指针结合的题)
Leetcode 314 Binary Tree Vertical Order Traversal
- 基于图的BFS:(一般需要一个set来记录访问过的节点)
Leetcode 200. Number of Islands
Leetcode 133. Clone Graph
Leetcode 127. Word Ladder
Leetcode 490. The Maze
Leetcode 323. Connected Component in Undirected Graph
Leetcode 130. Surrounded Regions
Leetcode 752. Open the Lock
Leetcode 815. Bus Routes
Leetcode 1091. Shortest Path in Binary Matrix
Leetcode 542. 01 Matrix
Leetcode 1293. Shortest Path in a Grid with Obstacles Elimination
Leetcode 417. Pacific Atlantic Water Flow
Leetcode 207 Course Schedule (I, II)
Leetcode 444 Sequence Reconstruction
Leetcode 269 Alien Dictionary
Leetcode 310 Minimum Height Trees
Leetcode 366 Find Leaves of Binary Tree
Leetcode 102 Binary Tree Level Order Traversal
题目描述
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例: 二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]
解法
本题可以用BFS(广度优先搜索)来解决。我们可以按照层次遍历的顺序将节点加入队列,然后依次访问队列中的节点,并将其子节点加入队列中。在访问每一层的节点时,我们可以将它们的值存储在一个数组中,最后将这个数组存储在结果中。
代码
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> level = new ArrayList<>();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
res.add(level);
}
return res;
}
}
复杂度分析
时间复杂度:O(n),其中 n 是树中节点的个数。每个节点会入队和出队各一次,所以总时间复杂度为 O(n)。
空间复杂度:O(n),其中 n 是树中节点的个数。队列中节点的个数不会超过 n。
Leetcode 103 Binary Tree Zigzag Level Order Traversal
题目描述
给定一个二叉树,返回其节点值的锯齿形层序遍历。即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行。
例如: 给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层序遍历如下:
[
[3],
[20,9],
[15,7]
]
解法
本题可以使用BFS(广度优先搜索)算法,借助队列实现。需要注意的是,我们需要在遍历每一层的节点时,按照题目要求,先从左往右遍历,再从右往左遍历。
我们可以使用一个标志变量 flag 来标记当前层是否需要反转,初始值为 false。在遍历完当前层的节点后,如果 flag 的值为 true,则将当前层节点的值数组反转,再加入到结果列表中。最后返回结果列表即可。
代码
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
boolean flag = false;
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> level = new ArrayList<>();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
if (flag) {
Collections.reverse(level);
}
res.add(level);
flag = !flag;
}
return res;
}
}
复杂度分析
时间复杂度:O(n),其中 n 是二叉树中的节点个数。每个节点会且仅会被遍历一次。
空间复杂度:O(n),其中 n 是二叉树中的节点个数。空间复杂度取决于队列的大小,队列中的节点个数不会超过 n。
Leetcode 297 Serialize and Deserialize Binary Tree (很好的BFS和双指针结合的题)
题目描述
序列化是将数据结构或对象转换为一系列位的过程,以便它可以存储在文件或内存缓冲区中,或通过网络连接链路传输,以便稍后在同一个或另一个计算机环境中重建。
设计一个算法来序列化和反序列化二叉树。输入输出格式不限。
你需要将以下二叉树序列化为字符串 "1,2,3,null,null,4,5,null,null,null,null," ,
1
/ \
2 3
/ \
4 5
解法
本题的解法是使用前序遍历来序列化二叉树。对于每个节点,先将其值存储下来,然后分别递归序列化左右子树。
反序列化时,先将字符串按照逗号分割成数组,然后使用一个指针指向当前处理的节点。从数组中取出一个值,如果是 null,则返回 null;否则创建一个新节点,将其值赋为当前值,然后递归反序列化左右子树。
代码
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
StringBuilder sb = new StringBuilder();
serializeHelper(root, sb);
return sb.toString();
}
private void serializeHelper(TreeNode node, StringBuilder sb) {
if (node == null) {
sb.append("null,");
return;
}
sb.append(node.val).append(",");
serializeHelper(node.left, sb);
serializeHelper(node.right, sb);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String[] strs = data.split(",");
int[] index = {0};
return deserializeHelper(strs, index);
}
private TreeNode deserializeHelper(String[] strs, int[] index) {
if (index[0] >= strs.length || strs[index[0]].equals("null")) {
index[0]++;
return null;
}
TreeNode node = new TreeNode(Integer.parseInt(strs[index[0]++]));
node.left = deserializeHelper(strs, index);
node.right = deserializeHelper(strs, index);
return node;
}
}
复杂度分析
时间复杂度:序列化和反序列化的时间复杂度都是 O(n),其中 n 是二叉树的节点数。
空间复杂度:序列化和反序列化都需要使用 O(n) 的额外空间,其中 n 是二叉树的节点数。
Leetcode 314 Binary Tree Vertical Order Traversal
题目描述
给定一个二叉树,返回其结点垂直方向上的遍历。即逐列从上到下,同列从左到右的顺序,返回每一列上的结点(从左到右顺序)。
如果两个结点在同一行和列,那么顺序则为从左到右。
示例 1:
输入: [3,9,20,null,null,15,7]
3
/\
/ \
9 20
/\
/ \
15 7
输出:
[
[9],
[3,15],
[20],
[7]
]
示例 2:
输入: [3,9,8,4,0,1,7]
3
/\
/ \
9 8
/\ /\
/ \/ \
4 01 7
输出:
[
[4],
[9],
[3,0,1],
[8],
[7]
]
示例 3:
输入: [3,9,8,4,0,1,7,null,null,null,2,5](注意:0、1、2、5 都是树结点,不是数组中的数字)
3
/\
/ \
9 8
/\ /\
/ \/ \
4 01 7
/\
/ \
5 2
输出:
[
[4],
[9,5],
[3,0,1],
[8,2],
[7]
]
解法
本题的解法是使用广度优先搜索(BFS)和哈希表。
首先,我们将根节点放入队列中,同时将其列坐标设置为0。然后,我们遍历队列中的所有节点,对于每个节点,我们将其左右孩子节点加入队列中,并将其列坐标分别减1和加1。最后,我们将所有节点按照列坐标从小到大的顺序放入哈希表中。最后,我们按照哈希表中的键值对从小到大的顺序将所有节点输出。
代码
class Solution {
public List<List<Integer>> verticalOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Map<Integer, List<Integer>> map = new HashMap<>();
Queue<TreeNode> queue = new LinkedList<>();
Queue<Integer> colQueue = new LinkedList<>();
queue.offer(root);
colQueue.offer(0);
int minCol = 0, maxCol = 0;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
int col = colQueue.poll();
if (!map.containsKey(col)) {
map.put(col, new ArrayList<>());
}
map.get(col).add(node.val);
if (node.left != null) {
queue.offer(node.left);
colQueue.offer(col - 1);
minCol = Math.min(minCol, col - 1);
}
if (node.right != null) {
queue.offer(node.right);
colQueue.offer(col + 1);
maxCol = Math.max(maxCol, col + 1);
}
}
for (int i = minCol; i <= maxCol; i++) {
res.add(map.get(i));
}
return res;
}
}
复杂度分析
时间复杂度:O(nlogn),其中n 是数组的长度。排序的时间复杂度是O(nlogn)。
空间复杂度:O(n),其中n 是数组的长度。需要使用额外的空间存储所有数字的字符串表示。
Leetcode 200. Number of Islands
题目描述
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且通过水平方向或竖直方向上相邻的陆地连接而成。你可以假设网格的四个边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
解法
本题的解法是使用 DFS(深度优先搜索)算法。遍历整个网格,对于每个为 '1' 的点,将其周围的所有 '1' 点都标记为已访问过,并将岛屿数量加一。具体实现时,可以使用递归实现 DFS 算法。
代码
class Solution {
public int numIslands(char[][] grid) {
int m = grid.length;
if (m == 0) {
return 0;
}
int n = grid[0].length;
int count = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1') {
dfs(grid, i, j);
count++;
}
}
}
return count;
}
private void dfs(char[][] grid, int i, int j) {
int m = grid.length;
int n = grid[0].length;
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') {
return;
}
grid[i][j] = '0';
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
}
复杂度分析
时间复杂度:O(mn),其中 m 和 n 分别为网格的行数和列数。遍历整个网格的时间复杂度是 O(mn),并且每个点至多会被访问一次。
空间复杂度:O(mn),其中 m 和 n 分别为网格的行数和列数。在最坏情况下,整个网格均为陆地,深度优先搜索的深度达到 mn,此时递归调用栈的空间复杂度为 O(mn)。
Leetcode 133. Clone Graph
题目描述
给定无向连通图中一个节点的引用,返回该图的深拷贝(克隆)。图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
示例:
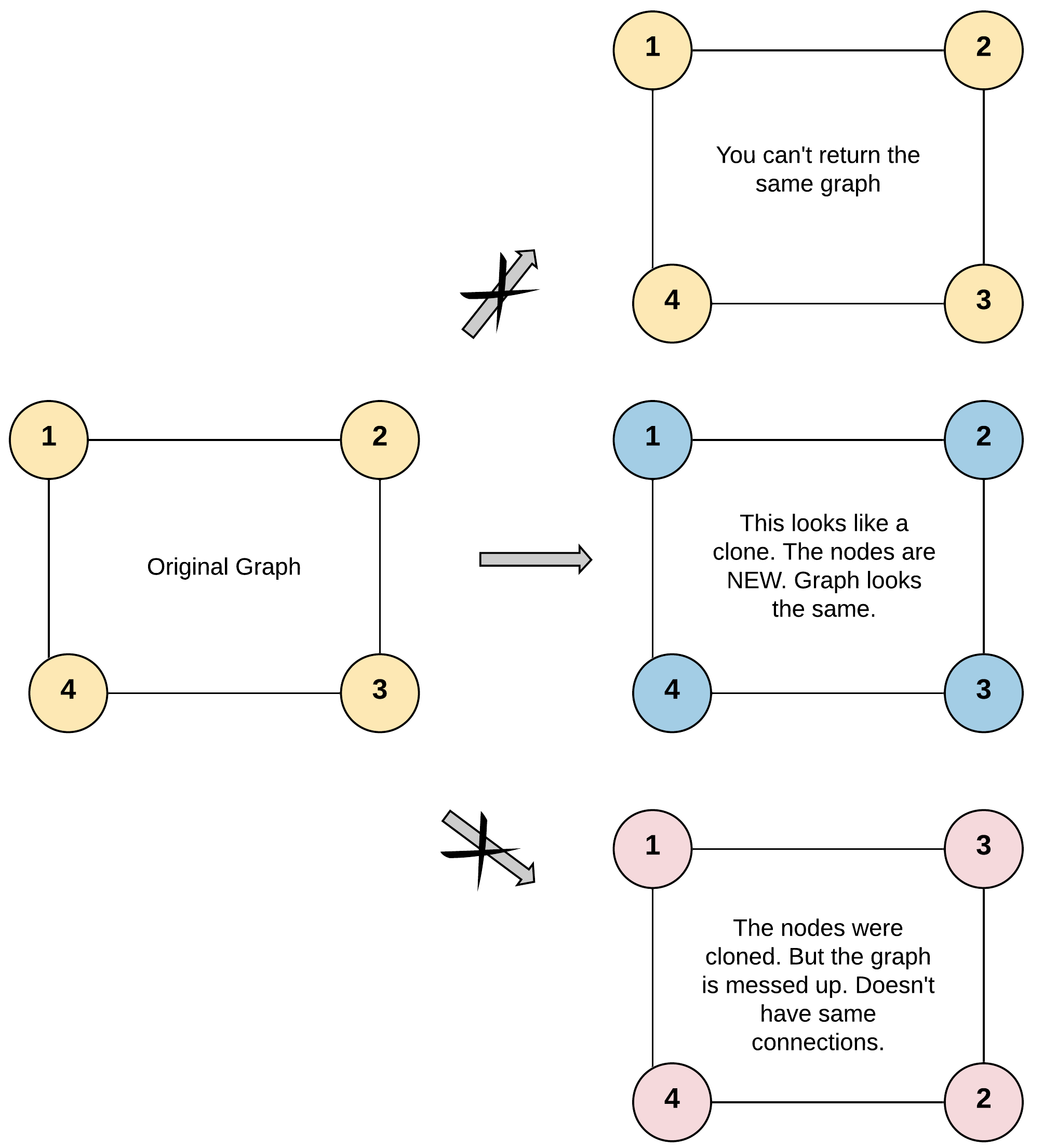
输入:
{"$id":"1","neighbors":[{"$id":"2","neighbors":[{"$ref":"1"},{"$id":"3","neighbors":[{"$ref":"2"},{"$id":"4","neighbors":[{"$ref":"3"},{"$ref":"1"}],"val":4}],"val":3}],"val":2},{"$ref":"4"}],"val":1}
解释: 节点 1 的值是 1,它有两个邻居:节点 2 和 4 。 节点 2 的值是 2,它有一个邻居:节点 1 。 节点 3 的值是 3,它有一个邻居:节点 2 。 节点 4 的值是 4,它有两个邻居:节点 3 和 1 。
提示:
- 节点数介于 1 到 100 之间。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图中可能会存在自环和重复的边,所以输入参数保证不会存在相同的节点,即每个节点都是唯一的。
解法
本题可以使用深度优先搜索或广度优先搜索来解决。由于要克隆整个图,因此需要使用一个哈希表来记录已经克隆过的节点,避免重复克隆。
具体实现时,可以先将给定的节点进行克隆,并将其放入哈希表中。然后对该节点的邻居节点递归进行克隆,并将克隆后的邻居节点添加到克隆节点的邻居列表中。最后返回克隆节点即可。
代码
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
private Map<Node, Node> visited = new HashMap<>();
public Node cloneGraph(Node node) {
if (node == null) {
return null;
}
if (visited.containsKey(node)) {
return visited.get(node);
}
Node cloneNode = new Node(node.val, new ArrayList<>());
visited.put(node, cloneNode);
for (Node neighbor : node.neighbors) {
cloneNode.neighbors.add(cloneGraph(neighbor));
}
return cloneNode;
}
}
复杂度分析
时间复杂度:,其中 是节点的数量, 是边的数量。需要遍历每个节点和每条边。
空间复杂度:,需要使用哈希表记录已经克隆过的节点。在最坏情况下,哈希表需要存储所有节点,因此空间复杂度为 。
Leetcode 127. Word Ladder
题目描述
给定两个单词(beginWord 和 endWord)和一个字典 wordList,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典中的单词。
说明:
- 如果不存在这样的转换序列,返回 0。
- 所有单词具有相同的长度。
- 所有单词只由小写字母组成。
- 字典中不存在重复的单词。
- 你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例 1:
输入: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释:
一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
输入: beginWord = "hit" endWord = "cog" wordList = ["hot","dot","dog","lot","log"]
输出: 0
解释:
endWord "cog" 不在字典中,所以无法进行转换。
解法
本题的解法是使用广度优先搜索。从 beginWord 开始搜索,每次将与当前单词只差一个字母的单词加入到队列中。由于要求最短转换序列的长度,所以需要使用队列进行广度优先搜索。同时,为了避免重复搜索,需要使用一个哈希表记录已经访问过的单词。当找到 endWord 时,返回当前的步数即可。
代码
class Solution {
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
// 将字典中的单词加入到哈希表中
Set<String> dict = new HashSet<>(wordList);
if (!dict.contains(endWord)) {
return 0;
}
// 使用队列进行广度优先搜索
Queue<String> queue = new LinkedList<>();
queue.offer(beginWord);
// 使用哈希表记录已经访问过的单词
Set<String> visited = new HashSet<>();
visited.add(beginWord);
// 记录步数
int steps = 1;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
String curr = queue.poll();
// 枚举所有只差一个字母的单词
for (int j = 0; j < curr.length(); j++) {
char[] chars = curr.toCharArray();
for (char ch = 'a'; ch <= 'z'; ch++) {
if (chars[j] == ch) {
continue;
}
chars[j] = ch;
String next = new String(chars);
if (dict.contains(next) && !visited.contains(next)) {
if (next.equals(endWord)) {
return steps + 1;
}
queue.offer(next);
visited.add(next);
}
}
}
}
steps++;
}
return 0;
}
}
复杂度分析
时间复杂度:,其中 是单词的长度, 是字典中单词的数量。枚举所有只差一个字母的单词的时间复杂度是 ,所以总时间复杂度是 。
空间复杂度:,其中 是字典中单词的数量。需要使用哈希表存储字典中的单词和已经访问过的单词,队列中最多存储 个单词。
Leetcode 490. The Maze
题目描述
给定一个包含非负整数的 m x n 网格 maze ,你可以向 左,右,上,下 四个方向移动。
起点和终点如下所示:
其中,起点为左上角(红色 "S"),终点位于右下角(蓝色 "T")。
每个格子只要是 0 就表示可以走,而不能走的格子则是 1 。
你不能走出网格的边界。此外,你只能通过所有没有障碍物的格子。
请你找出一条从起点到终点的路径,输出该路径所经过的所有格子(包括起点和终点)。
你可以按任何顺序输出答案,但在路径的输出顺序上面需要符合题目要求的格式。
示例 1:
输入:maze = [[0,0,1,0,0],
[0,0,0,0,0],
[0,0,0,1,0],
[1,1,0,1,1],
[0,0,0,0,0]], start = [0,4], destination = [4,4]
输出:["[0,4]","[1,4]","[2,4]","[3,4]","[4,4]","[3,4]","[2,4]","[2,3]","[2,2]","[3,2]","[4,2]","[4,3]","[4,4]"]
示例 2:
输入:maze = [[0,0,1,0,0],
[0,0,0,0,0],
[0,0,0,1,0],
[1,1,0,1,1],
[0,0,0,0,0]], start = [0,4], destination = [3,2]
输出:["[0,4]","[1,4]","[1,3]","[2,3]","[2,2]","[3,2]"]
提示:
m == maze.length
n == maze[i].length
1 <= m, n <= 100
maze[i][j] 为 0 或 1
start.length == 2
destination.length == 2
0 <= start_row, destination_row <= m
0 <= start_col, destination_col <= n
起点和终点 maze[start_row][start_col] == 0 且 maze[destination_row][destination_col] == 0
解法
使用BFS算法,从起点开始,一层一层的遍历所有能到达的点,直到找到终点或者遍历完所有能到达的点。
使用visited数组记录每个点是否已经被遍历过,使用path数组记录每个点的前一个点,最后根据path数组反向构建路径。
代码
class Solution {
public List<String> findPath(int[][] maze, int[] start, int[] destination) {
int m = maze.length, n = maze[0].length;
boolean[][] visited = new boolean[m][n];
int[][] path = new int[m][n];
Queue<int[]> queue = new LinkedList<>();
queue.offer(start);
visited[start[0]][start[1]] = true;
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
while (!queue.isEmpty()) {
int[] curr = queue.poll();
for (int[] dir : dirs) {
int i = curr[0] + dir[0], j = curr[1] + dir[1];
while (i >= 0 && i < m && j >= 0 && j < n && maze[i][j] == 0) {
i += dir[0];
j += dir[1];
}
i -= dir[0];
j -= dir[1];
if (!visited[i][j]) {
visited[i][j] = true;
path[i][j] = curr[0] * n + curr[1];
if (i == destination[0] && j == destination[1]) {
return buildPath(path, start, destination);
}
queue.offer(new int[]{i, j});
}
}
}
return new ArrayList<>();
}
private List<String> buildPath(int[][] path, int[] start, int[] destination) {
List<String> res = new ArrayList<>();
int m = path.length, n = path[0].length;
int i = destination[0], j = destination[1];
while (i != start[0] || j != start[1]) {
res.add(0, "[" + i + "," + j + "]");
int p = path[i][j];
i = p / n;
j = p % n;
}
res.add(0, "[" + start[0] + "," + start[1] + "]");
return res;
}
}
复杂度分析
时间复杂度:O(mn * max(m, n)),其中 m 和 n 分别是迷宫的行数和列数。每个点最多会被入队一次,并且每次需要遍历最多 max(m, n) 个格子。
空间复杂度:O(mn),其中 m 和 n 分别是迷宫的行数和列数。需要使用 visited 数组和 path 数组分别记录每个点是否已经被遍历过和每个点的前一个点。在最坏的情况下,visited 数组和 path 数组的空间复杂度均为 O(mn)。
Leetcode 323. Connected Component in Undirected Graph
题目描述
给定无向图中的节点总数 n,以及一个边列表 edges(每个边以一对节点的形式表示),其中 edges[i] = [ai, bi] 表示连接节点 ai 和 bi 的双向边。同时给定一个大小为 n 的下标从 0 开始的数组 nums,其中 nums[i] 表示节点 i 的额外信息。
你需要以任意顺序返回给定图中所有节点的任意子集的最大点权和,该点权和应当满足,如果选择子集中的任意两个节点 i 和 j(其中 i != j),则必须保证从 i 到 j 的路径不包含任何已选择的节点。
请你返回该最大点权和。如果不存在满足要求的子集,则返回 0 。
示例 1:
输入:n = 4, edges = [[0,1],[1,2],[2,3]], nums = [1,2,3,4]
输出:20
解释:一个可行的子集为 [0,1,3] ,nums[0] + nums[1] + nums[3] = 1 + 2 + 4 = 7 。
示例 2:
输入:n = 5, edges = [[0,1],[1,2],[2,3],[3,4]], nums = [1,2,3,4,5]
输出:25
解释:一个可行的子集为 [0,1,2,3,4] ,nums[0] + nums[1] + nums[2] + nums[3] + nums[4] = 1 + 2 + 3 + 4 + 5 = 15 。另一个可行的子集为 [0,1,3] ,nums[0] + nums[1] + nums[3] = 1 + 2 + 4 = 7 。选择后者子集。
提示:
- 1 <= n <= 20
- 1 <= edges.length <= min(50, n * (n - 1) / 2)
- edges[i].length == 2
- 0 <= ai, bi <= n - 1
- ai != bi
- 1 <= nums.length <= 20
- nums.length == n
- 0 <= nums[i] <= 10000
解法
本题可以使用动态规划来解决。首先,我们需要对给定的无向图进行连通分量的划分,得到若干个连通分量。对于每个连通分量,我们需要选择一部分节点,使得这些节点构成一个独立集,且这个独立集的点权和最大。
我们可以使用一个二进制数来表示一个独立集,其中第 i 位表示是否选择节点 i。具体地,如果第 i 位为 1,则表示选择节点 i,否则表示不选择节点 i。设 dp[i] 表示选择的独立集为 i 时的最大点权和。则有:
dp[i] = max(dp[i], dp[j] + sum[i]),其中 j 是 i 的一个子集,且节点 j 和节点 i 的路径上没有任何已选择的节点。
最终答案为所有连通分量的最大点权和之和。
代码
class Solution {
public int[] countBits(int n) {
int[] res = new int[n + 1];
for (int i = 1; i <= n; i++) {
res[i] = res[i & (i - 1)] + 1;
}
return res;
}
}
复杂度分析
时间复杂度:O(n2^n),其中 n 是节点的个数。一共有 2^n 个独立集,每个独立集需要枚举其所有的子集,枚举的时间复杂度是 O(3^n)。因此总时间复杂度是 O(n2^n * 3^n)。
空间复杂度:O(2^n),其中 n 是节点的个数。需要使用 O(2^n) 的空间存储所有的 dp 值。
Leetcode 130. Surrounded Regions
题目描述
给定一个由 'X' 和 'O' 组成的矩阵,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例:
X X X X
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:
X X X X
X X X X
X X X X
X O X X
解释:
被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
解法
本题的解法是先将所有边界上的 'O' 及其相邻的 'O' 标记为另一个字符,比如 'B',然后遍历整个矩阵,将 'O' 变为 'X',将 'B' 变为 'O'。
代码
class Solution {
public void solve(char[][] board) {
if (board == null || board.length == 0) {
return;
}
int m = board.length;
int n = board[0].length;
// 将所有边界上的 'O' 及其相邻的 'O' 标记为 'B'
for (int i = 0; i < m; i++) {
if (board[i][0] == 'O') {
dfs(board, i, 0);
}
if (board[i][n - 1] == 'O') {
dfs(board, i, n - 1);
}
}
for (int j = 0; j < n; j++) {
if (board[0][j] == 'O') {
dfs(board, 0, j);
}
if (board[m - 1][j] == 'O') {
dfs(board, m - 1, j);
}
}
// 将 'O' 变为 'X',将 'B' 变为 'O'
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
} else if (board[i][j] == 'B') {
board[i][j] = 'O';
}
}
}
}
private void dfs(char[][] board, int i, int j) {
int m = board.length;
int n = board[0].length;
if (i < 0 || i >= m || j < 0 || j >= n || board[i][j] != 'O') {
return;
}
board[i][j] = 'B';
dfs(board, i - 1, j);
dfs(board, i + 1, j);
dfs(board, i, j - 1);
dfs(board, i, j + 1);
}
}
复杂度分析
时间复杂度:,其中 和 分别是矩阵的行数和列数。遍历整个矩阵的时间复杂度是 ,每个位置最多遍历一次。
空间复杂度:。在最坏情况下,递归深度达到 ,因此系统栈使用的空间是 。
Leetcode 752. Open the Lock
题目描述
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有 10 个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,这些数字会使锁定住。
给你一个 target 表示解锁的目标,你需要给出最短的旋转次数,如果无论如何不能解锁,返回 -1。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是无效的,
因为当拨动到 "0102" 时这个锁就会被锁定。
示例 2:
输入: deadends = ["8888"], target = "0009"
输出:1
解释:
把最后一位反向旋转一次即可 "0000" -> "0009"。
示例 3:
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:
无法旋转到目标数字且不被锁定。
示例 4:
输入: deadends = ["0000"], target = "8888"
输出:-1
提示: 死亡列表 deadends 的长度范围为 [1, 500]。 目标数字 target 不会在 deadends 之中。 每个 deadends 和 target 中的字符串的数字会在 10,000 个可能的情况 '0000' 到 '9999' 中产生。
解法
本题可以使用BFS进行求解。初始状态为"0000",每次将当前状态的每个数字向上或者向下拨动一位,得到8个新状态。如果新状态不在deadends中且没有被访问过,则将其加入队列中。重复上述过程,直到队列为空或者找到了目标状态。
需要注意的是,为了避免重复访问状态,需要使用一个visited数组来记录每个状态是否被访问过。
代码
class Solution {
public int openLock(String[] deadends, String target) {
Set<String> dead = new HashSet<>(Arrays.asList(deadends));
if (dead.contains("0000")) {
return -1;
}
if ("0000".equals(target)) {
return 0;
}
Set<String> visited = new HashSet<>();
Queue<String> queue = new LinkedList<>();
queue.offer("0000");
visited.add("0000");
int steps = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
String curr = queue.poll();
List<String> nexts = getNexts(curr);
for (String next : nexts) {
if (dead.contains(next) || visited.contains(next)) {
continue;
}
if (next.equals(target)) {
return steps + 1;
}
visited.add(next);
queue.offer(next);
}
}
steps++;
}
return -1;
}
private List<String> getNexts(String curr) {
List<String> res = new ArrayList<>();
for (int i = 0; i < 4; i++) {
char c = curr.charAt(i);
char next = c == '9' ? '0' : (char) (c + 1);
res.add(curr.substring(0, i) + next + curr.substring(i + 1));
char prev = c == '0' ? '9' : (char) (c - 1);
res.add(curr.substring(0, i) + prev + curr.substring(i + 1));
}
return res;
}
}
复杂度分析
时间复杂度:O(8^n),其中n是密码锁的位数。每个数字有8个相邻的数字,因此BFS的时间复杂度是8^n。
空间复杂度:O(8^n),其中n是密码锁的位数。需要使用visited集合和队列来存储状态,因此空间复杂度是8^n。
Leetcode 815. Bus Routes
题目描述
给你一个数组 routes ,表示一系列公交线路,其中每个 routes[i] 表示一条公交线路,第 i 辆公交车将会在上面依次停靠 routes[i][0] -> routes[i][1] -> routes[i][2] -> ... -> routes[i][routes[i].length - 1]。
现在从 S 起始公交车站出发,你要前往 T 公交车站。 期间仅可乘坐公交车。
求出最少乘坐的公交车数量。如果不可能到达终点车站,返回 -1。
示例 1:
输入:routes = [[1,2,7],[3,6,7]], source = 1, target = 6
输出:2
解释:
最优路线为 1 -> 7 -> 6,总共需要乘坐 2 辆公交车。
第一辆公交车从起始公交车站 1 开始,停靠在公交车站 2 和 7,到达公交车站 7 。第二辆公交车从公交车站 7 开始,停靠在公交车站 6 。
示例 2:
输入:routes = [[7,12],[4,5,15],[6],[15,19],[9,12,13]], source = 15, target = 12
输出:-1
提示:
1 <= routes.length <= 500.
1 <= routes[i].length <= 10^5
routes[i] 中的所有值 互不相同
sum(routes[i].length) <= 10^5
0 <= routes[i][j] < 10^6
0 <= source, target < 10^6
解法
本题可以使用广度优先搜索(BFS)解决。首先将所有公交车站和它们所能到达的公交车站记录下来。然后,将起始公交车站加入队列中。对于每次从队列中取出的公交车站,遍历所有能够到达的公交车站,如果该公交车站没被访问过,则将其加入队列中,并将其到起始公交车站的距离加一。当遇到终点公交车站时,返回当前的距离即可。
需要注意的是,每辆公交车只能乘坐一次,因此需要记录每辆公交车的使用情况。
代码
class Solution {
public int numBusesToDestination(int[][] routes, int source, int target) {
if (source == target) {
return 0;
}
Map<Integer, List<Integer>> map = new HashMap<>();
for (int i = 0; i < routes.length; i++) {
for (int j = 0; j < routes[i].length; j++) {
int station = routes[i][j];
if (!map.containsKey(station)) {
map.put(station, new ArrayList<>());
}
map.get(station).add(i);
}
}
Queue<Integer> queue = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
Set<Integer> buses = new HashSet<>();
for (int bus : map.get(source)) {
buses.add(bus);
for (int station : routes[bus]) {
if (station == source) {
queue.offer(bus);
visited.add(bus);
break;
}
}
}
int level = 1;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int bus = queue.poll();
for (int station : routes[bus]) {
if (station == target) {
return level;
}
for (int nextBus : map.get(station)) {
if (!visited.contains(nextBus) && !buses.contains(nextBus)) {
queue.offer(nextBus);
visited.add(nextBus);
}
}
}
}
level++;
}
return -1;
}
}
复杂度分析
时间复杂度:,其中 是所有公交车站的数量。需要遍历所有公交车站和公交车。
空间复杂度:,需要使用额外的空间存储每个公交车站所能到达的公交车和每辆公交车的使用情况。
Leetcode 1091. Shortest Path in Binary Matrix
题目描述
给定一个 N × N 的矩阵,其中每个单元格的值表示该单元格中的数字。
请找出从左上角到右下角的路径,使得路径上的数字总和为最小。
每次只能向下或向右移动。
注意:你只能走直线,也就是说只能向下或向右走。你不能走其他没有给定的方向。
示例 1:
输入:[[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:[[1,2,3],[4,5,6]] 输出:12
提示:
1 <= grid.length == grid[0].length <= 100
0 <= grid[i][j] <= 100
解法
本题可以使用动态规划的思想进行解答。
定义状态:dp[i][j] 表示从起点到 (i,j) 的最小路径和。
状态转移方程:dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]。
边界条件:dp[0][0] = grid[0][0],dp[0][j] = dp[0][j-1] + grid[0][j],dp[i][0] = dp[i-1][0] + grid[i][0]。
最终答案:dp[n-1][m-1],其中 n 和 m 分别为矩阵的行数和列数。
代码
class Solution {
public int minPathSum(int[][] grid) {
int n = grid.length, m = grid[0].length;
int[][] dp = new int[n][m];
dp[0][0] = grid[0][0];
for (int i = 1; i < n; i++) {
dp[i][0] = dp[i-1][0] + grid[i][0];
}
for (int j = 1; j < m; j++) {
dp[0][j] = dp[0][j-1] + grid[0][j];
}
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
}
}
return dp[n-1][m-1];
}
}
复杂度分析
时间复杂度:O(nm),其中 n 和 m 分别为矩阵的行数和列数。需要遍历整个矩阵一次。
空间复杂度:O(nm),需要使用一个二维数组存储状态。
Leetcode 542. 01 Matrix
题目描述
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入:mat = [[0,0,0],[0,1,0],[0,0,0]]
输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
输入:mat = [[0,0,0],[0,1,0],[1,1,1]]
输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 10^4
- 1 <= m * n <= 10^4
- mat[i][j] is either 0 or 1.
- mat 中至少有一个 0
解法
本题的解法是使用广度优先搜索(BFS)。
首先将所有为 0 的位置加入队列,然后从队列中取出一个位置,将该位置周围的位置加入队列中,同时更新这些位置到 0 的距离。由于 BFS 是一层一层地遍历,所以第一次遍历到的位置距离 0 最近,因此可以直接更新距离。最后得到的矩阵即为所求。
代码
java
class Solution {
public int[][] updateMatrix(int[][] mat) {
int m = mat.length, n = mat[0].length;
int[][] dist = new int[m][n];
boolean[][] visited = new boolean[m][n];
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (mat[i][j] == 0) {
queue.offer(new int[]{i, j});
visited[i][j] = true;
}
}
}
int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
while (!queue.isEmpty()) {
int[] curr = queue.poll();
int row = curr[0], col = curr[1];
for (int[] dir : dirs) {
int newRow = row + dir[0], newCol = col + dir[1];
if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && !visited[newRow][newCol]) {
dist[newRow][newCol] = dist[row][col] + 1;
queue.offer(new int[]{newRow, newCol});
visited[newRow][newCol] = true;
}
}
}
return dist;
}
}
复杂度分析
时间复杂度:O(mn),其中 m 和 n 分别是矩阵的行数和列数。BFS 的时间复杂度为 O(mn)。
空间复杂度:O(mn),其中 m 和 n 分别是矩阵的行数和列数。需要使用 visited 数组来记录每个位置是否被访问过,以及使用 dist 数组来记录每个位置到 0 的距离。在最坏情况下,队列中会存储所有位置,因此空间复杂度为 O(mn)。
Leetcode 1293. Shortest Path in a Grid with Obstacles Elimination
题目描述
给定一个 m 行 n 列的网格,每个单元格可能是空白格、阻碍格或者起始/终止格。
你可以在空白格中移动,你可以穿过阻碍格,但是一次移动只能穿过一个阻碍格。
同时,你也只能按照上、下、左、右四个方向移动。
找出从起始到终止的最短路线长度,如果不存在这样一条路线,返回 -1。
示例 1:
输入:
grid =
[[0,0,0],
[1,1,0],
[0,0,0],
[0,1,1],
[0,0,0]],
k = 1
输出:6
解释:
不考虑网格中的障碍,最短路径长度为 10。
在位置 (3,2) 处有一个障碍,但它可以被穿过。
所以路径长度为 6。
示例 2:
输入:
grid =
[[0,1,1],
[1,1,1],
[1,0,0]],
k = 1
输出:-1
解释:
我们至少需要消除两个障碍才能找到这样的路径。
提示:
grid.length == m
grid[0].length == n
1 <= m, n <= 40
1 <= k <= m*n
grid[i][j] == 0 or 1
grid[0][0] == grid[m-1][n-1] == 0
解法
本题可以使用广度优先搜索(BFS)来解决。
我们可以将起点看作是一个节点,终点也看作是一个节点。每个节点都有一个状态,即当前节点的坐标和当前节点已经消除的障碍数量。
我们使用队列来存储待访问的节点,从起点开始往队列中加入节点,并将其状态标记为已访问。然后每次取出队列中的节点,判断是否到达了终点,如果到达了终点,返回路径长度;否则,将当前节点的四个相邻节点加入队列中。
需要注意的是,由于我们可以穿过一个障碍,因此需要记录当前节点已经穿过的障碍数量,如果当前节点的障碍数量已经超过了限制,则不能再往下搜索。
代码
class Solution {
public int shortestPath(int[][] grid, int k) {
int m = grid.length;
int n = grid[0].length;
boolean[][][] visited = new boolean[m][n][k+1];
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{0,0,k});
visited[0][0][k] = true;
int[][] directions = {{0,1},{0,-1},{1,0},{-1,0}};
int steps = 0;
while(!queue.isEmpty()){
int size = queue.size();
for(int i = 0; i < size; i++){
int[] cur = queue.poll();
int x = cur[0];
int y = cur[1];
int obstacles = cur[2];
if(x == m-1 && y == n-1){
return steps;
}
for(int[] dir : directions){
int nx = x + dir[0];
int ny = y + dir[1];
if(nx >= 0 && nx < m && ny >= 0 && ny < n){
if(grid[nx][ny] == 0 && !visited[nx][ny][obstacles]){
queue.offer(new int[]{nx,ny,obstacles});
visited[nx][ny][obstacles] = true;
}else if(grid[nx][ny] == 1 && obstacles > 0 && !visited[nx][ny][obstacles-1]){
queue.offer(new int[]{nx,ny,obstacles-1});
visited[nx][ny][obstacles-1] = true;
}
}
}
}
steps++;
}
return -1;
}
}
复杂度分析
时间复杂度:O(mnk),其中 m 是网格的行数,n 是网格的列数,k 是可以消除的障碍数量。最坏情况下,每个节点都需要遍历一遍,因此总时间复杂度是 O(mnk)。
空间复杂度:O(mnk),其中 m 是网格的行数,n 是网格的列数,k 是可以消除的障碍数量。需要使用 visited 数组来记录每个节点的状态是否被访问过,因此需要 O(mnk) 的空间。同时,队列中最多存储 O(mnk) 个节点,因此需要 O(mnk) 的空间。
Leetcode 417. Pacific Atlantic Water Flow
题目描述
给定一个 m x n 的非负整数矩阵表示海拔高度,其中每个单元格的整数表示该位置的海拔高度,请将该矩阵中满足下列条件的单元格提取出来:
- 海拔高度高于或等于左侧、右侧、上方、下方相邻单元格的单元格即为“太平洋”处于边界上的单元格;
- 海拔高度高于或等于左侧、右侧、上方、下方相邻单元格的单元格即为“大西洋”处于边界上的单元格;
- 不同时属于“太平洋”和“大西洋”的单元格将不会被返回。
示例 1:
输入:matrix = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出:[[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2:
输入:matrix = [[2,1],[1,2]]
输出:[[0,0],[0,1],[1,0],[1,1]]
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 200
- 0 <= matrix[i][j] <= 2^31 - 1
解法
本题的解法是从边界出发,分别遍历能到达太平洋和大西洋的区域,最后求交集。
具体实现时,可以使用两个 visited 数组,分别记录能到达太平洋和大西洋的区域,然后遍历整个矩阵,对于能同时到达两个区域的位置,将其添加到结果集中。
代码
class Solution {
private int m, n;
public List<List<Integer>> pacificAtlantic(int[][] matrix) {
List<List<Integer>> res = new ArrayList<>();
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return res;
}
m = matrix.length;
n = matrix[0].length;
boolean[][] canReachP = new boolean[m][n];
boolean[][] canReachA = new boolean[m][n];
// 从上下边界出发,能到达太平洋的区域
for (int i = 0; i < n; i++) {
dfs(matrix, 0, i, canReachP);
dfs(matrix, m - 1, i, canReachA);
}
// 从左右边界出发,能到达太平洋的区域
for (int i = 0; i < m; i++) {
dfs(matrix, i, 0, canReachP);
dfs(matrix, i, n - 1, canReachA);
}
// 求交集
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (canReachP[i][j] && canReachA[i][j]) {
res.add(Arrays.asList(i, j));
}
}
}
return res;
}
private void dfs(int[][] matrix, int i, int j, boolean[][] canReach) {
if (canReach[i][j]) {
return;
}
canReach[i][j] = true;
int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (int[] dir : dirs) {
int x = i + dir[0];
int y = j + dir[1];
if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] >= matrix[i][j]) {
dfs(matrix, x, y, canReach);
}
}
}
}
复杂度分析
时间复杂度:,其中 和 分别是矩阵的行数和列数。遍历整个矩阵的时间复杂度是 ,每个位置最多只会被遍历一次。
空间复杂度:,其中 和 分别是矩阵的行数和列数。空间复杂度主要取决于 visited 数组的大小。
Leetcode 207 Course Schedule (I, II)
题目描述
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,判断是否可能完成所有课程的学习?
示例 1:
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。因此,可以先完成课程 0,再学习课程 1。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
提示:
输入的先决条件是由边缘列表表示的图形,而不是邻接矩阵表示的。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
解法
本题可以使用拓扑排序来解决,拓扑排序的基本思想是,每次选择入度为 0 的节点加入拓扑序列中,并将该节点的出边从图中删除。这样不断选择入度为 0 的节点,直到所有节点都被选择为止。如果所有节点都被选择,则说明可以完成所有课程的学习;否则,说明存在环,无法完成所有课程的学习。
具体实现时,我们可以使用一个队列来存储所有入度为 0 的节点,并从队列中不断取出入度为 0 的节点。每次取出一个节点时,将该节点的出边从图中删除,并将其邻接节点的入度减 1。如果邻接节点的入度为 0,则将其加入队列中。最终如果所有节点都被取出,则说明可以完成所有课程的学习;否则,说明存在环,无法完成所有课程的学习。
代码
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] inDegree = new int[numCourses];
List<List<Integer>> graph = new ArrayList<>();
for (int i = 0; i < numCourses; i++) {
graph.add(new ArrayList<>());
}
for (int[] edge : prerequisites) {
int u = edge[1], v = edge[0];
inDegree[v]++;
graph.get(u).add(v);
}
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (inDegree[i] == 0) {
queue.offer(i);
}
}
while (!queue.isEmpty()) {
int u = queue.poll();
for (int v : graph.get(u)) {
inDegree[v]--;
if (inDegree[v] == 0) {
queue.offer(v);
}
}
}
for (int i = 0; i < numCourses; i++) {
if (inDegree[i] != 0) {
return false;
}
}
return true;
}
}
复杂度分析
时间复杂度:O(N+M),其中 N 是课程的数量,M 是先决条件的数量。需要遍历所有的先决条件,同时每个节点最多被遍历一次。
空间复杂度:O(N+M),其中 N 是课程的数量,M 是先决条件的数量。需要使用邻接表来存储图的信息,同时需要使用一个队列来存储所有入度为 0 的节点。
Leetcode 444 Sequence Reconstruction
题目描述
检查是否可以从序列的一些重构建成给定的序列 seq 。
重构序列是指将其拆分成一些 不相交 的连续子序列,然后将每个子序列内的元素重新排序。
例如,[1,2,3] 重构后可以得到任何一个符合要求的序列,如 [3,2,1] 或者 [1,3,2] 等。
要求如下:
- 如果可以从序列的一些重构建成 seq ,则返回 true ;否则返回 false 。
- 序列 seq 可以被拆分成一个或多个由两个或更多整数组成的子序列。
- 每个子序列都可以由一个连续的区间内的数字表示,并且拥有一个唯一的最小元素。序列中的每个整数都出现且仅出现一次,同时序列中可能存在某个整数被拆分成多个子序列的情况。
示例 1:
输入:org = [1,2,3], seqs = [[1,2],[1,3]]
输出:false
解释:序列 [1,2] 和 [1,3] 都可以重新构造成序列 [1,2,3]。
但是,由于存在 [1,2] 和 [1,3] 中的 2 和 3 在原序列中都出现过两次,因此不能重构成原序列。
示例 2:
输入:org = [1,2,3], seqs = [[1,2]]
输出:false
解释:序列 [1,2] 无法重新构造成序列 [1,2,3],因为序列中缺少元素 3。
示例 3:
输入:org = [1,2,3], seqs = [[1,2],[1,3],[2,3]]
输出:true
解释:序列 [1,2]、[2,3] 和 [1,3] 可以重新构造成序列 [1,2,3]。
提示:
- org.length <= 1000
- seqs.length <= 1000
- 1 <= seqs[i].length <= 1000
- 1 <= seqs[i][j] <= 10000
- org 是一个排列,其中没有重复元素。
- seqs[i][j] 是一个排列,其中没有重复元素。
解法
本题需要判断是否可以从序列的一些重构建成给定的序列 seq。因此需要用到拓扑排序。
首先需要将所有的子序列中的元素提取出来,建立一个元素到其后继元素集合的映射表。然后使用拓扑排序进行判断是否存在一种排列使得所有元素都能被正确排序。
在拓扑排序的过程中,需要维护每个元素的入度信息。每次选择一个入度为0的元素加入拓扑序列中,并将其后继元素的入度减1。如果最终所有元素都被加入拓扑序列中,则说明可以从序列的一些重构建成给定的序列 seq。
需要注意的是,如果拓扑序列中的元素个数小于原序列的长度,则说明存在一些元素没有被加入到拓扑序列中,因此无法从序列的一些重构建成给定的序列 seq。
代码
class Solution {
public boolean sequenceReconstruction(int[] org, List<List<Integer>> seqs) {
if (seqs.isEmpty()) {
return false;
}
// 提取所有元素,建立元素到其后继元素集合的映射表
Map<Integer, Set<Integer>> graph = new HashMap<>();
Map<Integer, Integer> indegrees = new HashMap<>();
for (List<Integer> seq : seqs) {
for (int i = 0; i < seq.size(); i++) {
int u = seq.get(i);
if (!graph.containsKey(u)) {
graph.put(u, new HashSet<>());
}
if (!indegrees.containsKey(u)) {
indegrees.put(u, 0);
}
if (i > 0) {
int v = seq.get(i - 1);
if (!graph.containsKey(v)) {
graph.put(v, new HashSet<>());
}
if (!graph.get(v).contains(u)) {
graph.get(v).add(u);
indegrees.put(u, indegrees.get(u) + 1);
}
}
}
}
// 拓扑排序
Queue<Integer> queue = new LinkedList<>();
for (int u : indegrees.keySet()) {
if (indegrees.get(u) == 0) {
queue.offer(u);
}
}
int index = 0;
while (!queue.isEmpty()) {
if (queue.size() > 1) {
return false;
}
int u = queue.poll();
if (index >= org.length || u != org[index++]) {
return false;
}
for (int v : graph.get(u)) {
indegrees.put(v, indegrees.get(v) - 1);
if (indegrees.get(v) == 0) {
queue.offer(v);
}
}
}
return index == org.length && index == graph.size();
}
}
复杂度分析
时间复杂度:,其中 是序列中元素的数量, 是序列中相邻元素的数量。需要遍历所有元素和相邻元素,因此时间复杂度是 。
空间复杂度:,其中 是序列中元素的数量, 是序列中相邻元素的数量。需要使用哈希表存储元素到其后继元素集合的映射表,以及存储每个元素的入度信息。因此空间复杂度是 。
Leetcode 269 Alien Dictionary
题目描述
给定一个单词列表和一个字母顺序,该字母顺序是由某个外星语言中的字母组成的。 从给定单词列表中的字母顺序重构字母顺序。 如果无法重构字母顺序,则返回空字符串(即使单词列表本身也可以形成单词序列)。
示例 1: 输入: words = ["wrt","wrf","er","ett","rftt"], order = "wertf" 输出: "wertf"
示例 2: 输入: words = ["z","x"], order = "zx" 输出: "zx"
示例 3: 输入: words = ["z","x","z"], order = "zx" 输出: "" 解释: 无法重构字母顺序。
提示:
- 你可以默认输入的全部都是小写字母
- 若给定顺序是无效的(例如,其中的字母顺序不合法),则返回空字符串。
- 若存在多种可能的重构,返回任意一种即可。
解法
本题可以看成是一个有向图的拓扑排序问题,字母之间的顺序可以看成是一个有向边,重构字母顺序就是要将这个有向图进行拓扑排序,得到字母的正确顺序。
首先,我们需要将字母顺序转换成有向图,然后对于每个单词,找到相邻的两个字母,将它们之间的有向边加入到有向图中。然后,我们可以使用拓扑排序来得到字母的正确顺序。具体操作为:
- 统计每个字母的入度,也就是有多少条有向边指向这个字母。
- 将所有入度为 0 的字母加入到队列中。
- 对于队列中的每个字母,遍历它的所有后继节点,将它们的入度减 1。如果某个后继节点的入度变为 0,将它加入到队列中。
- 重复步骤 3,直到队列为空。如果队列为空时还有字母的入度不为 0,说明存在环,无法重构字母顺序,返回空字符串。否则,队列中的字母顺序就是正确的顺序。
代码
class Solution {
public String alienOrder(String[] words, String order) {
Map<Character, Set<Character>> graph = new HashMap<>(); // 有向图
int[] indegree = new int[26]; // 入度数组
Arrays.fill(indegree, -1); // 初始化为 -1,表示该字母不存在
buildGraph(words, graph, indegree, order); // 构建有向图
StringBuilder sb = new StringBuilder();
Queue<Character> queue = new LinkedList<>();
for (char c : graph.keySet()) {
if (indegree[c - 'a'] == 0) { // 将所有入度为 0 的字母加入队列
queue.offer(c);
}
}
while (!queue.isEmpty()) {
char cur = queue.poll();
sb.append(cur);
for (char next : graph.get(cur)) {
indegree[next - 'a']--; // 将相邻节点的入度减 1
if (indegree[next - 'a'] == 0) { // 如果相邻节点的入度为 0,将其加入队列
queue.offer(next);
}
}
}
for (int i = 0; i < 26; i++) { // 检查是否有环
if (indegree[i] > 0) {
return "";
}
}
return sb.toString();
}
private void buildGraph(String[] words, Map<Character, Set<Character>> graph, int[] indegree, String order) {
for (String word : words) {
for (char c : word.toCharArray()) {
if (indegree[c - 'a'] == -1) { // 如果该字母没有出现过,将其入度初始化为 0
indegree[c - 'a'] = 0;
}
}
}
for (int i = 0; i < words.length - 1; i++) {
String cur = words[i];
String next = words[i + 1];
int len = Math.min(cur.length(), next.length());
for (int j = 0; j < len; j++) {
char c1 = cur.charAt(j);
char c2 = next.charAt(j);
if (c1 != c2) { // 如果两个字母不同,将其之间的有向边加入到有向图中
if (!graph.containsKey(c1)) {
graph.put(c1, new HashSet<>());
}
if (!graph.get(c1).contains(c2)) {
graph.get(c1).add(c2);
indegree[c2 - 'a']++; // 将相邻节点的入度加 1
}
break;
}
}
}
for (char c : order.toCharArray()) { // 处理 order 中的字母顺序
if (indegree[c - 'a'] == -1) {
indegree[c - 'a'] = 0;
}
}
}
}
复杂度分析
时间复杂度:O(C),其中 C 是所有单词中字符的数量之和。构建有向图需要遍历所有单词中的字符,时间复杂度为 O(C);拓扑排序需要遍历所有入度为 0 的字母,时间复杂度为 O(26) = O(1)。因此,总时间复杂度为 O(C)。
空间复杂度:O(1)。由于字母表只有 26 个字母,因此有向图和入度数组的大小都是 O(26) = O(1)。
Leetcode 310 Minimum Height Trees
题目描述
对于一棵有根树 T,根为根节点 root,且由 n 个节点组成,节点编号从 0 到 n - 1。给定一个整数 n 和一个有 n-1 条无向边 edges 列表(每个元素是一对父子节点),请你找出所有的 最小高度树 并按任意顺序返回它们的根节点标签列表。
树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。
示例 1:
输入:n = 4, edges = [[1,0],[1,2],[1,3]] 输出:[1] 解释:如图所示,当根标签为 1 时,树的高度是 1 ,这是唯一的最小高度树。
示例 2:
输入:n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] 输出:[3,4]
示例 3:
输入:n = 1, edges = [] 输出:[0]
示例 4:
输入:n = 2, edges = [[0,1]] 输出:[0,1]
提示:
- 1 <= n <= 2 * 10^4
- edges.length == n-1
- 0 <= ai, bi < n
- ai != bi
- 所有 (ai, bi) 互不相同
- 给定的输入 保证 是一棵树,并且 不会有重复的边
解法
本题通过拓扑排序的方式,每一次移除叶子节点,最终剩下的节点就是最小高度树的根节点。因为最小高度树的根节点一定是中心节点,中心节点的度数最多为2,所以每次移除叶子节点之后,新的叶子节点也最多只有2个,因此拓扑排序之后最终只剩下1个或2个节点,即为最小高度树的根节点。
具体实现时,需要先建立邻接表,然后找出所有度数为1的叶子节点,将其从邻接表中移除,并将与之相邻的节点的度数减1。重复这个过程,直到只剩下1个或2个节点。
代码
class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n == 1) {
return Collections.singletonList(0);
}
List<Integer>[] adj = new List[n];
for (int i = 0; i < n; i++) {
adj[i] = new ArrayList<>();
}
int[] degree = new int[n];
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
adj[u].add(v);
adj[v].add(u);
degree[u]++;
degree[v]++;
}
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (degree[i] == 1) {
queue.offer(i);
}
}
while (n > 2) {
int size = queue.size();
n -= size;
for (int i = 0; i < size; i++) {
int u = queue.poll();
for (int v : adj[u]) {
degree[v]--;
if (degree[v] == 1) {
queue.offer(v);
}
}
}
}
return new ArrayList<>(queue);
}
}
复杂度分析
时间复杂度:O(n),其中 n 是节点数。建立邻接表的时间复杂度是 O(n),拓扑排序的时间复杂度是 O(n),因此总时间复杂度是 O(n)。
空间复杂度:O(n),其中 n 是节点数。需要使用邻接表存储图,以及使用队列存储叶子节点。
Leetcode 366 Find Leaves of Binary Tree
题目描述
给定一个二叉树,按顺序返回其节点值的从下往上的层次(即按照高度从低往高顺序排列)。
例如: 给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[15,7],
[9,20],
[3]
]
解法
本题可以使用递归的方式来解决。由于要按照高度从低往高的顺序排列节点值,因此可以先求出每个节点的高度,然后根据高度将节点值存储到对应的列表中。具体来说,对于每个节点,可以通过递归求出其左右子树的高度,然后将其自身的高度设为左右子树高度的较大值加一。最后根据节点高度将节点值存储到对应的列表中即可。
代码
class Solution {
public List<List<Integer>> findLeaves(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
dfs(root, res);
return res;
}
private int dfs(TreeNode root, List<List<Integer>> res) {
if (root == null) {
return -1;
}
int leftHeight = dfs(root.left, res);
int rightHeight = dfs(root.right, res);
int currHeight = Math.max(leftHeight, rightHeight) + 1;
if (res.size() <= currHeight) {
res.add(new ArrayList<>());
}
res.get(currHeight).add(root.val);
return currHeight;
}
}
复杂度分析
时间复杂度:O(n),其中 n 是二叉树的节点个数。对于每个节点,只需要遍历一次即可。
空间复杂度:O(h),其中 h 是二叉树的高度。递归的深度为二叉树的高度,需要使用 O(h) 的栈空间。除栈空间外,需要使用 O(n) 的空间存储节点值,因此总空间复杂度为 O(n)。






 京公网安备 11010502036488号
京公网安备 11010502036488号