链接：https://ac.nowcoder.com/acm/contest/3002/F
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

有一天，maki拿到了一颗树。所谓树，即没有自环、重边和回路的无向连通图。
这个树有 个顶点， 条边。每个顶点被染成了白色或者黑色。
maki想知道，取两个不同的点，它们的简单路径上有且仅有一个黑色点的取法有多少？
注：
①树上两点简单路径指连接两点的最短路。
② 和 的取法视为同一种。
 
 
 

输入描述:

第一行一个正整数n。代表顶点数量。

第二行是一个仅由字符'B'和'W'组成的字符串。第 i个字符是B代表第 i 个点是黑色，W代表第 i个点是白色。
接下来的n-1行，每行两个正整数 x ， y，代表 x 点和 y点有一条边相连

输出描述:

一个正整数，表示只经过一个黑色点的路径数量。
示例1

输入

复制 
3
WBW
1 2
2 3

输出

复制 
3

说明

树表示如下：
其中只有2号是黑色点。
<1,2>、<2,3>、<1,3>三种取法都只经过一个黑色点。
 
思路：
　　　对于可以连边的白色节点，用并查集把节点合并，并且在合并时更新连通块大小。
　　　对于一条含有黑色节点的路径，我们易知： 路径数 = 黑色节点相邻的 白连通块内点的size * 该点相连的白连通块点的size···
　　　
　　　所以只需要先求出白连通块的大小，然后对于黑点，只需要计算出黑点相邻白连通块加上其的后继连通块即可。
　　　后继白连通块大小求法：
　　　

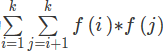
 　　　关于_find中为什么是sum += sz[r2]的问题，因为建的是无向图，不保证此时的fa[r1]一定是与fa[r2]相等的

 

　　

  1 #include <bits/stdc++.h>
  2 #define dbg(x) cout << #x << "=" << x << endl
  3 
  4 using namespace std;
  5 typedef long long LL;
  6 const int maxn = 1e6 + 7;
  7 
  8 int n;
  9 LL ans;
 10 int fa[maxn];
 11 int a[maxn];
 12 int head[maxn];
 13 char c[maxn];
 14 int cnt = 0;
 15 LL sz[maxn];
 16 LL num[maxn];
 17 int _count = 0;
 18 
 19 //vector <int> g[maxn];
 20 
 21 struct Edge {
 22     int to,nxt;
 23 }edge[maxn];
 24 
 25 void BuildGraph(int u, int v) {
 26     edge[cnt].to = v;
 27     edge[cnt].nxt = head[u];
 28     head[u] = cnt++;
 29 
 30     edge[cnt].to = u;
 31     edge[cnt].nxt = head[v];
 32     head[v] = cnt++;
 33 }
 34 
 35 void init()
 36 {
 37     memset(head, -1, sizeof(head));
 38     for(int i = 1; i <= n; i++) {
 39         fa[i] = i;
 40         sz[i] = 1;
 41     }
 42 }
 43 
 44 namespace _buff {
 45     const size_t BUFF = 1 << 19;
 46     char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
 47     char getc() {
 48         if (ib == ie) {
 49             ib = ibuf;
 50             ie = ibuf + fread(ibuf, 1, BUFF, stdin);
 51         }
 52         return ib == ie ? -1 : *ib++;
 53     }
 54 }
 55 
 56 int read() {
 57     using namespace _buff;
 58     int ret = 0;
 59     bool pos = true;
 60     char c = getc();
 61     for (; (c < '0' || c > '9') && c != '-'; c = getc()) {
 62         assert(~c);
 63     }
 64     if (c == '-') {
 65         pos = false;
 66         c = getc();
 67     }
 68     for (; c >= '0' && c <= '9'; c = getc()) {
 69         ret = (ret << 3) + (ret << 1) + (c ^ 48);
 70     }
 71     return pos ? ret : -ret;
 72 }
 73 
 74 int fid(int x)
 75 {
 76     int r = x;
 77     while(fa[r] != r) {
 78         r = fa[r];
 79     }
 80     int i,j;///路径压缩
 81     i = x;
 82     while(fa[i] != r) {
 83         j = fa[i];
 84         fa[i] =  r;
 85         i = j;
 86     }
 87     return r;
 88 }
 89 
 90 void join(int r1,int r2)///合并
 91 {
 92     int fidroot1 = fid(r1), fidroot2 = fid(r2);
 93     int root = min(fidroot1, fidroot2);
 94     sz[root] = sz[fidroot1] + sz[fidroot2];
 95     if(fidroot1 != fidroot2) {
 96         fa[fidroot2] = root;
 97         fa[fidroot1] = root;
 98     }
 99 }
100 
101 LL _find(int x) {
102     //dbg(x);
103     LL sum = 0;
104     for(int i = head[x]; ~i; i = edge[i].nxt) {
105         int v = edge[i].to;
106         if(a[v]) {
107             //num[v] = 0;
108             continue;
109         }
110         int r1 = fid(x), r2 = fid(v);
111         sum += sz[r2];
112         num[++_count] = sz[r2];
113     }
114     return sum;
115 }
116 
117 int main()
118 {
119     scanf("%d\n",&n);
120     init();
121     ans = 0;
122     scanf("%s",c);
123     for(int i = 0; i < n; ++i) {
124         if(c[i] == 'W') {
125             a[i+1] = 0;
126         }
127         else {
128             a[i+1] = 1;
129         }
130     }
131     for(int i = 1; i < n; ++i) {
132         int x, y;
133         scanf("%d %d",&x, &y);
134         BuildGraph(x,y);
135         if(!a[x] && !a[y]) {
136             join(x,y);
137         }
138     }
139     for(int i = 1; i <= n; ++i) {
140         if(a[i] == 0) continue;
141         _count = 0;
142         memset(num, 0, sizeof(num));
143         ans += _find(i);
144         for(int j = 1; j <= _count; ++j) {
145             for(int k = j+1; k <= _count; ++k) {
146                 ans += num[j] * num[k];
147             }
148         }
149     }
150 
151     printf("%lld\n",ans);
152 }
View Code