描述
题目描述
这个题目很简单, 就是一个简单的在一个数组中寻找第大的元素
解法
解法一: STL库函数
实现思路
直接调用我们的STL函数, 求取第大的元素
代码实现
class Solution {
public:
int findKth(vector<int> a, int n, int K) {
nth_element(a.begin(), a.begin() + K - 1, a.end(), greater<int>());
// 求取第k大的函数
return a[K - 1];
}
};
时空复杂度分析
时间复杂度:
理由如下: 这个函数只跟我们数组的大小有关系
空间复杂度:
理由如下: 我们未引入变量空间
解法二: 快速排序
实现思路
我们先把我们的数组排好序之后, 我们再进行输出第大的数
代码实现
class Solution {
public:
void quick_sort(vector<int> &q, int l, int r) {
if (l >= r) return;
// 递归的停止条件
int i = l - 1, j = r + 1, x = q[l + r >> 1];
// 分为子情况
while (i < j) {
do i++;
while (q[i] > x);
do j--;
while (q[j] < x);
if (i < j) swap(q[i], q[j]);
}
// 哨兵的移动交换
quick_sort(q, l, j), quick_sort(q, j + 1, r);
// 递归处理之后的问题
}
int findKth(vector<int> a, int n, int K) {
quick_sort(a, 0, n - 1);
return a[K - 1];
}
};
时空复杂度分析
时间复杂度:
理由如下: 因为我们执行的快速排序, 不断递归, 平均下来我们的时间复杂度就是
空间复杂度:
理由如下: 我们要考虑调用的递归栈的深度
解法三: 快速选择算法
实现思路:
其实我们的主要思想就是一个分治, 这里就是把我们快速排序的代码给优化了一下, 首先我们是划分一个分解点, 如图所示
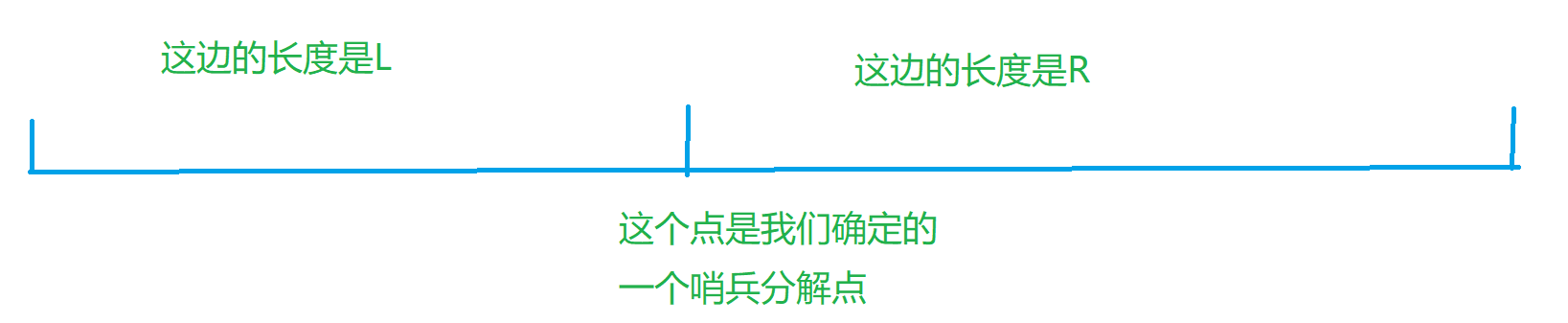
然后我们前面部分跟我们的快速排序的算法是一样的, 然后我们选定了一个作为我们的分界点之后, 我们就把比大的都放到左边, 比小的都放到右边, 然后我们可以得到左右区间的一个长度, 这里我们用表示我们左半区间的长度, 表示我们右半区间的长度
如果我们, 可以说明我们要找的是在我们的左半区间, 我们就可以只是递归我们的左半区间, 减少了右半区间的多余遍历
如果我们, 我们可以知道我们要找到的是在我们的右半区间, 我们可以只是递归我们的右半区间, 减少了左半区间的多余遍历
代码实现
class Solution {
public:
int quick_sort(vector<int> &q, int l, int r, int k) {
if (l >= r) return q[l];
// 到达了递归的终点, 我们返回最后的结果
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j) {
do i++;
while (q[i] > x);
do j--;
while (q[j] < x);
if (i < j) swap(q[i], q[j]);
}
// 快速排序, 根据我们的x, 把我们的区间划分为两部分
if (j - l + 1 >= k)
return quick_sort(q, l, j, k);
else
return quick_sort(q, j + 1, r, k - (j - l + 1));
// 把我们的区间长度和我们的k相比较, 看我们的k应该是在于哪一个区间, 少递归了一部分
}
int findKth(vector<int> a, int n, int K) {
return quick_sort(a, 0, n - 1, K);
}
};
时空复杂度分析
时间复杂度: 期望的时间复杂度:
理由如下: 首先我们先是不考虑我们的极端情况, 我们就是考虑一般情况, 那么我们第一次数组长度为, 然后我们第一次递归, 我们会遍历, 然后我们递归再次划分的时候, 我们会遍历, 以此类推, 最后我们把遍历的所有的相加, 我们可以知道这个数列是趋于的, 所以我们的时间复杂度均摊下来就是的, 但是其实快速选择算法跟快速排序算法一个很关键的问题就是他的一个基准点的选择, 这里参考算法导论的一个说明: 这个算法的最坏情况运行时间是, 即使找最小元素也是如此, 因为我们在每次划分的时候可能极不走运的总是按余下的元素中最大的来进行划分所以我们会出现最坏的情况, 这里如果想要优化可以考虑随机化的思想, 这题不做过多赘述
空间复杂度: 期望空间复杂度:
理由如下: 我们这里的空间复杂度跟我们上述的时间复杂度类似,当我们一切符合期望没有极端的最差的情况出现时,我们的空间复杂度期望就是,如果我们出现了我们上述的极端情况,那么我们递归栈的深度加深,我们的空间复杂度就会退化成为






 京公网安备 11010502036488号
京公网安备 11010502036488号