描述

题目描述

我们给定一个字符串的表达式, 我们的字符串中会有如下的几个有效字符

[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’， ‘)’,‘[’, ‘]’,‘{’ ,‘ }

然后让我们对我们的表达式求取值

题解

解法一：投机取巧

实现思路

这里我们讲一个投机取巧的做法，就是我们可以考虑用$PythonPython$来解决这个问题, 这里唯一需要注意的就是$PythonPython$中不识别我们的$[][]$和$\{\}$

那么我们就把他们都替换成为$()()$, 然后我们接下来就可以直接使用我们的$evaleval$函数求值, 最后把它转成整型就可以了

代码实现

str = input()

str = str.replace('[', '(').replace('{', '(').replace(']', ')').replace('}', ')')

print(int(eval(str)))

时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 我们还是需要遍历字符串把我们的括号进行一个替换

空间复杂度: $O(1)O(1)$

理由如下: 我们未使用额外的空间

解法二: 正常解法

实现思路

其实我们只是要遵从以下的几点, 这个题目我们其实就可以是迎刃而解了

1. 其实三种括号我们都可以看成是一种括号, 就是我们的小括号

   因为我们实际作用上来讲是没有区别的

2. 我们每次遇到括号我们就递归

   每一次递归我们就会脱掉一层括号

3. 我们用vector就可以实现栈的操作

图解代码

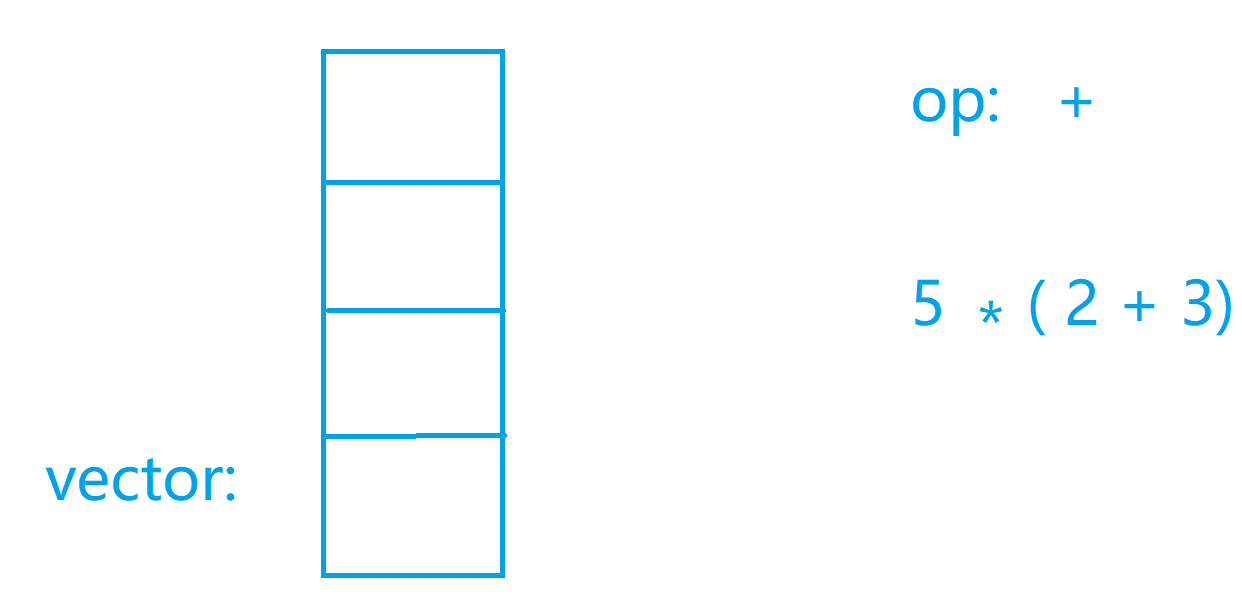
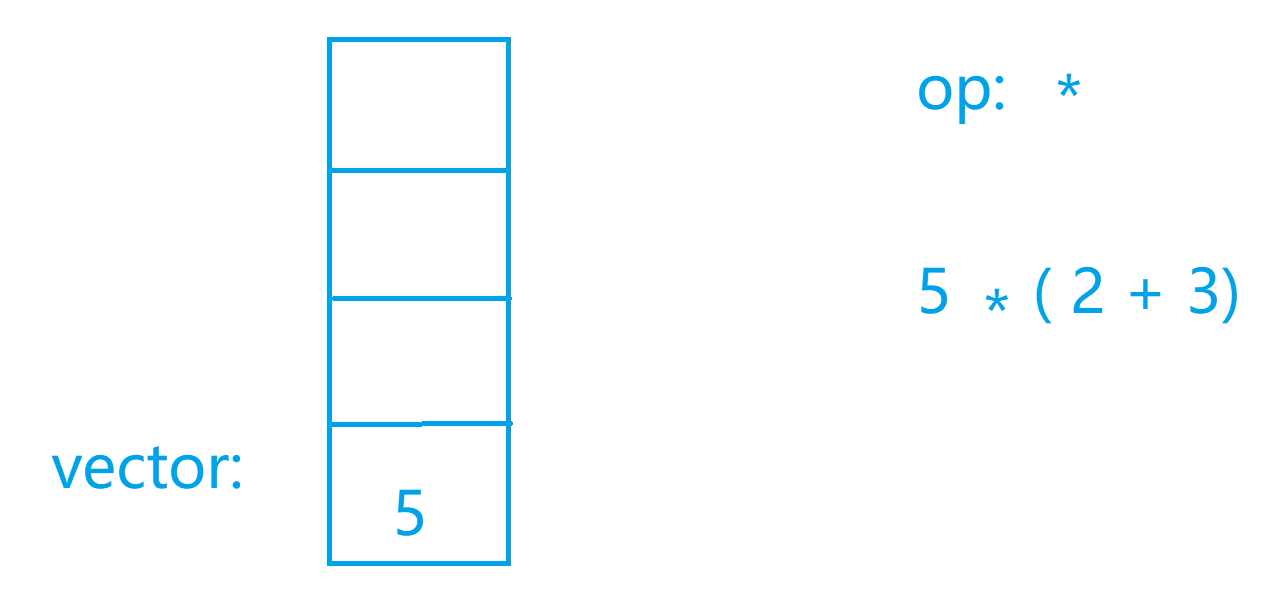
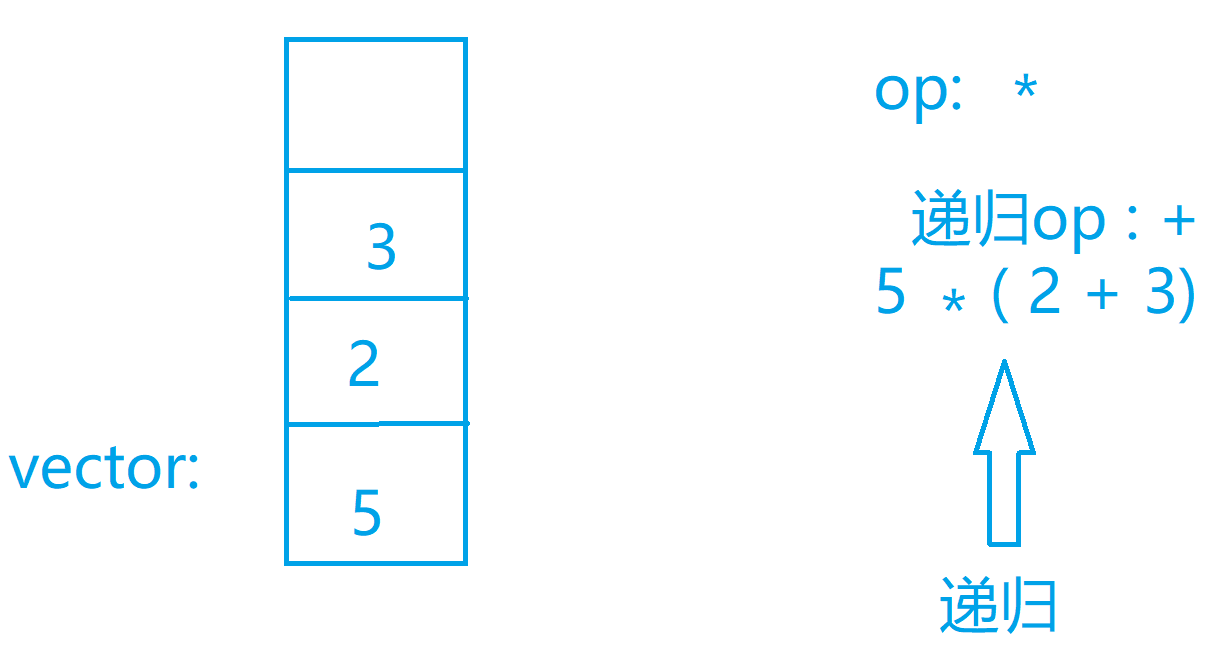
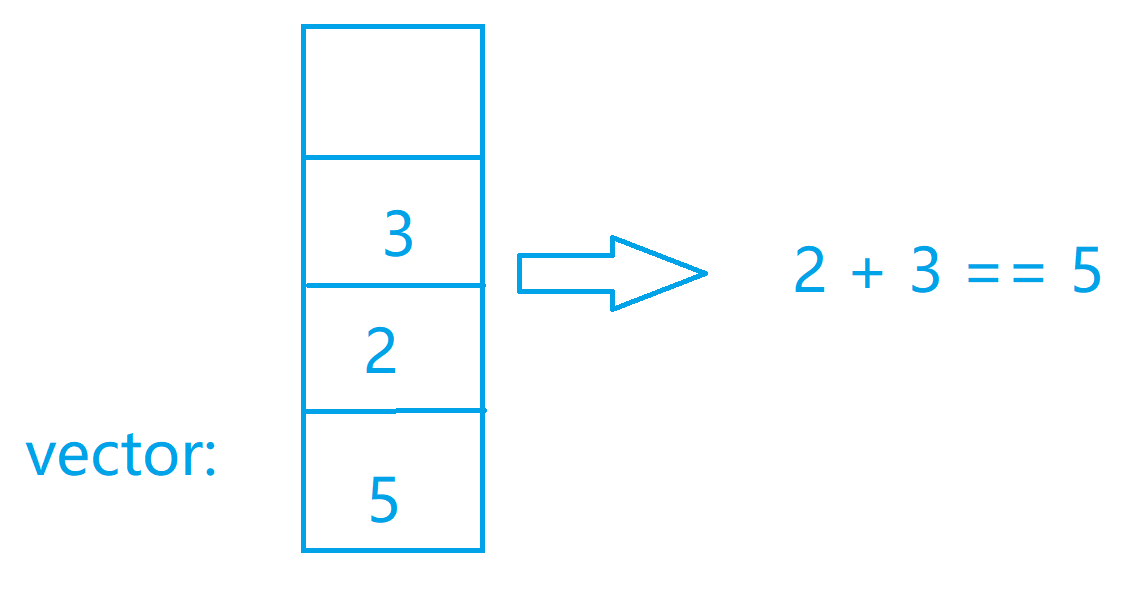
代码实现

#include <bits/stdc++.h>

using namespace std;

int dfs(string &s, int l, int r) {
    vector<int> st;
    // 这个代表的就是我们的栈
    int len = s.size(), res = 0;
    char op = '+';
    // c初始值是0, 假设初始的符号就是+
    for (int i = l; i <= r; i++) {
        if (isdigit(s[i])) res = res * 10 + (s[i] - '0');
        // 避免多位, 转换成为一个整数
        if (s[i] == '(' || s[i] == '[' || s[i] == '{') {
            int lv = 0;
            int j = i;
            for (; j <= r; j++) {
                if (s[j] == '(' || s[j] == '[' || s[j] == '{')
                    lv += 1;
                else if (s[j] == ')' || s[j] == ']' || s[j] == '}')
                    if (--lv == 0) break;
            }
            res = dfs(s, i + 1, j - 1);
            i = j + 1;
            // 如果是左括号, 我们继续向下递归, 如果我们不是左括号, 如果是右括号我们返回一层
        }
        if (!isdigit(s[i]) || i == r) {
            if (op == '+') {
                st.emplace_back(res);
            } else if (op == '-') {
                st.emplace_back(-res);
            } else if (op == '*') {
                st.back() *= res;
            } else if (op == '/') {
                st.back() /= res;
            }
            op = s[i];
            res = 0;
        }
        // 如果是符号位, 我们考虑出栈计算
    }
    return accumulate(st.begin(), st.end(), 0);
    // 返回整个的值
}

signed main() {
    string s;
    cin >> s;
    cout << dfs(s, 0, s.size() - 1) << "\n";
    return 0;
}

时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 我们会遍历一次我们的字符串

空间复杂度: $O(n)O(n)$

理由如下: 我们要考虑我们不断递归的递归栈的深度和我们每次的vector存了多少的东西