1. 四个基本子空间
- 行空间 C(AT),一个 Rn 的子空间,由所有行的线性组合构成,维数为 r
- 列空间 C(A),一个 Rm 的子空间,由所有列的线性组合构成,维数为 r
- 零空间 N(A),一个 Rn 的子空间,由所有 Ax=0 的解的线性组合构成,维数为 n−r
- 左零空间 N(AT),一个 Rm 的子空间,由所有 ATy=0 或者 yTA=0T 的解的线性组合构成,维数为 m−r
2. R 的四个基本子空间
假设 A 的最简行阶梯形式为 R,我们可以很容易地从 R 找到四个子空间。
矩阵 R 中有两个主元,因此其秩为 2。
行空间的维数等于秩,为 2,其中一个基可以取 R 的前两行。
列空间的维数等于秩,为 2,主元所在的列为第一列和第四列,因此其中一个基为 R 中对应的两列。
零空间的维数等于 n−r,为 3,有三个自由变量,因此对应着三个特解,它们就是零空间的一个基。
左零空间寻找的是 R 的行的线性组合来产生一个零向量。
显而易见, y1 和 y2 必须为 0,而 y3 可以取任意值。左零空间的一个基为 (0, 0, 1),维数为 m−r=1。
2. A 的四个基本子空间
R 和 A 有着相同的行空间、维数 r 和基。
EA=RA=E−1R
由矩阵乘法可知, R 的每一行都是对 A 的行的线性组合,而且 A 的每一行也都是对 R 的行的线性组合。因此,消元只是改变了行,并没有改变行空间。
Ax=0 当且仅当 Rx=0,它们的 r 个主列都是不相关的,它们的列空间维数都为 r。
其中 A 的列可以看作是对 E−1 的列的线性组合,因此 A 和 E−1 有着相同的列空间。
R 和 A 有着相同的零空间、维数和基,因为消元并不改变方程组的解。
A 的左零空间维数为 m−r。
因为 R 的最后 m−r 行为全零行,也就是 E 中最后 m−r 行对 A 的行的线性组合产生了零向量,因此它们是左零空间的一个基。
获取更多精彩,请关注「seniusen」!




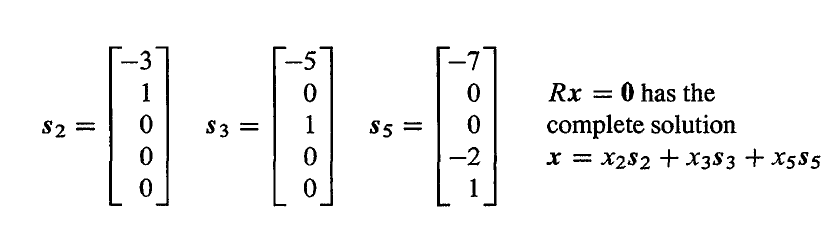




 京公网安备 11010502036488号
京公网安备 11010502036488号