描述

题目描述

给定我们一个排列, 排列的顺序就是我们的入栈的顺序, 然后我们需要入栈顺序不变的情况下, 使得我们的字典序最大

题解

解法一: 记录

实现思路

这里我们可以很容易的发现, 如果想要我们的字典序最大, 那么我们一定是要构成的排列第一个一定是我们的$nn$, 然后之后尽可能的获取最大的值, 那么我们应该怎么想呢?

假设我们预处理出来了给定我们的那个排列的每一个位置后面比他大的最大的数, 然后我们每次入栈的时候, 一定要保证每次出去最大的数字, 那么我们很容易就是可以想到, 只要我们没到达我们当前的位置后面最大的那个数字的时候, 我们就要一直向我们的答案数组里面塞入数字, 这样才是一个最优的解法

那最大的数字我们应该怎么求取呢, 我们可以采用递推的方式求取我们最大的这个数字, 然后这里用图解演示一下

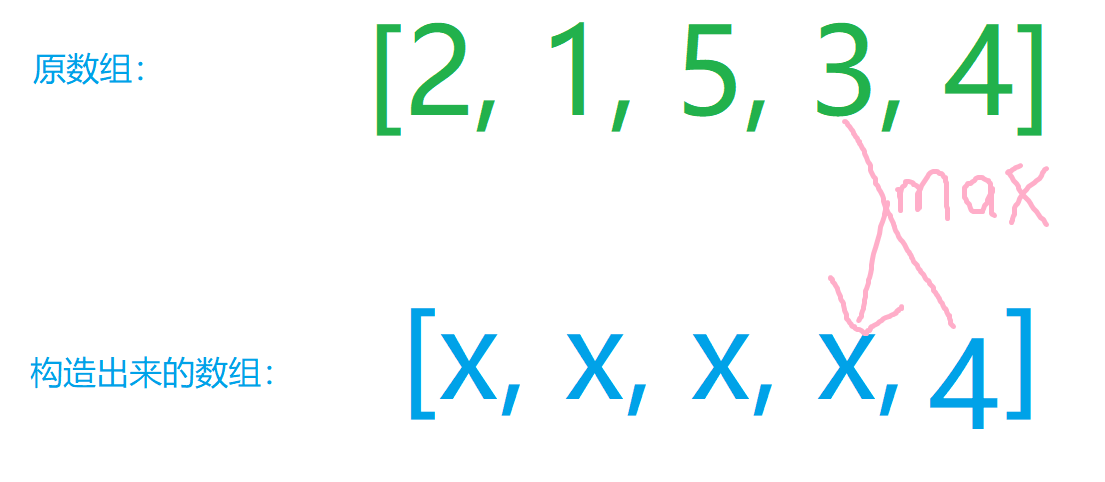
然后我们按照这样的方式, 进行一个递推可以得到这样的数组

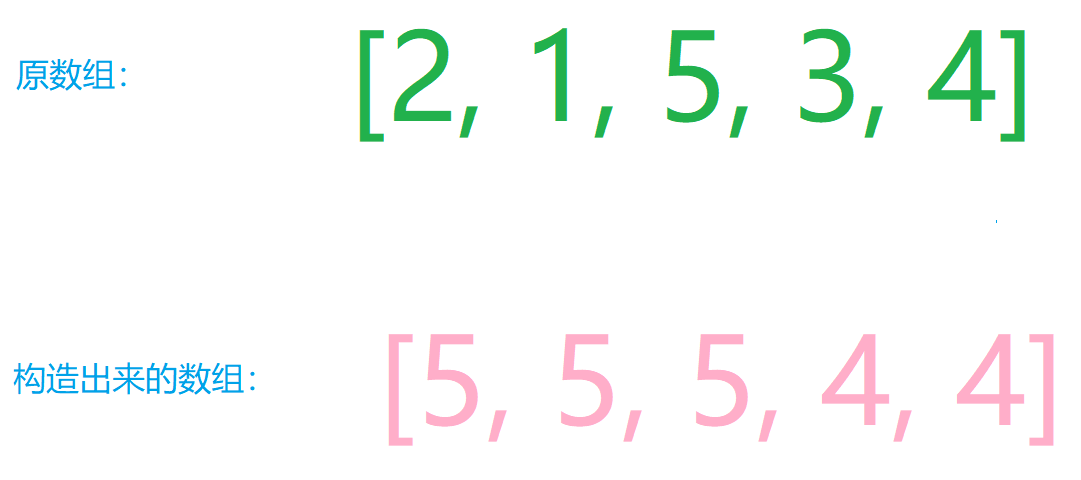
代码实现

class Solution {
   public:
    vector<int> solve(int* a, int aLen) {
        stack<int> st;
        vector<int> dp(aLen, 0), res(aLen, 0);
        int idx = 0;
        dp[aLen - 1] = a[aLen - 1];
        for (int i = aLen - 2; i >= 0; i--) dp[i] = max(a[i], dp[i + 1]);
        // 获得我们每一个元素后面的最大值
        for (int i = 0; i < aLen; i++) {
            while (st.size() and st.top() >= dp[i]) {
                res[idx++] = st.top();
                st.pop();
            }
            st.push(a[i]);
//             后插入是避免造成影响
//             我们一直放到这个值后面的最大值为止
        }
        while (st.size()) {
            res[idx++] = st.top();
            st.pop();
        }
//         如果最后不空的话，按照顺序放入我们的答案数组
        return res;
    }
};

时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 我们遍历了整个数组

空间复杂度: $O(n)O(n)$

理由如下: 开辟了一个辅助的数组

解法二

实现思路

跟我们做法一的思路差不多, 我们开一个标记数组, 用于记录我们的栈中有哪些元素, 然后我们定义一个最大值, 用于获取我们当前要找的最大值, 然后如果最大值在栈中, 我们不断出栈, 如果不在我们的栈中, 我们继续入栈直到最大值出现位置

代码实现

class Solution {
   public:
    vector<int> solve(int* a, int aLen) {
        stack<int> st;
        vector<int> res(aLen, 0);
        // 答案数组
        int idx = 0, maxx = aLen;
        // idx是我们每次插入的下标, maxx是我们要找的最大值
        bitset<50010> bt = 0;
        // 优化空间的标记数组
        for (int i = 0; i < aLen; i++) {
            st.push(a[i]);
            bt[a[i]] = 1;
            while (maxx and bt[maxx]) maxx--;
            // 当我们的n存在, 并且是在我们的栈中, 然后一直找到我们目前从大到小在栈中的元素
            for (;st.size() and maxx <= st.top();) {
                res[idx++] = st.top();
                st.pop();
            }
            // 把我们当前在栈内大的元素全部存入
        }
        while (st.size()) {
            res[idx++] = st.top();
            st.pop();
        }
//         如果栈内还有值，存入答案数组
        return res;
    }
};

时空复杂度分析

时间复杂度: $O(n)O(n)$

理由如下: 我们遍历了整个数组

空间复杂度: $O(n)O(n)$

理由如下: 开辟了一个辅助的数组