2020牛客暑期多校训练营（第五场）D

题目描述

Inaka composes music. Today's arrangement includes a chord of $n$ notes that are pairwise distinct, represented by a permutation $p_1,p_2,\cdots,p_n$ of integers from $1$ to $n$ (inclusive) denoting the notes from the lowest to the highest.
Her friend, Miyako, sneaks in and plays a trick by altering the chord with the following two operations. $\text{Drop-2}$ : Take out the second highest note and move it to the lowest position, i.e. change the permutation to $p_{n-1}, p_1, p_2, \cdots, p_{n-3}, p_{n-2}, p_n$ . Invert: Take out the lowest note and move it to the highest position, i.e. change the permutation to $p_2, p_3, \dots, p_{n-1}, p_n, p_1$ .
Any number of consecutive $\text{Drop-2}$ operations is considered a multi-drop. Miyako would like to change the permutation to an ordered permutation, $1, 2, \cdots, n$ , in the fewest number of $\text{multi-drops}$ possible. Please help her find the number of $\text{multi-drops}$ needed.

输入描述

The first line contains an integer $n$ $(2 \leqslant n \leqslant 500)$ — the number of notes.
The second line contains n space-separated integers $p_1, p_2, \cdots, p_n$ — the original permutation of notes.
The input guarantees each integer from $1$ to $n$ (inclusive) appears in the permutation exactly once.

输出描述

Output one integer — the number of $\text{multi-drops}$ required to change the permutation to an ordered one.

示例1

输入

6
2 4 5 1 3 6

输出

说明

An optimal solution with two multi-drops is:
Invert, $5$ times, changing the permutation to $6,2,4,5,1,3$ ;
$\text{Drop-2}$ , $3$ times, changing the permutation to $4,5,1,6,2,3$ ;
$\text{Invert}$ , $4$ times, changing the permutation to $2,3,4,5,1,6$ ;
$\text{Drop-2}$ , $1$ time, changing the permutation to $1,2,3,4,5,6$ .

示例2

输入

8
8 4 7 3 6 2 5 1

输出

分析

对于操作 $\text{Drop-2}$ ，可以将 $p_1\sim p_{n-1}$ 看作一个环，环的长度为 $n-1$ ，即进行 $n-1$ 次操作 $\text{Drop-2}$ ，排列还原；对于操作 $\text{Invert}$ ，可以将 $p_1\sim p_n$ 看作一个环，环的长度为 $n$ ，即进行 $n$ 次操作 $\text{Invert}$ ，排列还原。形成的两个环如图所示， $\color{red}\surd$ 代表当前排列 $p$ 的第一个数， $\color{red}\times$ 代表位于大环（长度为 $n$ 的环）上，而在小环（长度为 $n-1$ 的环）外的数。

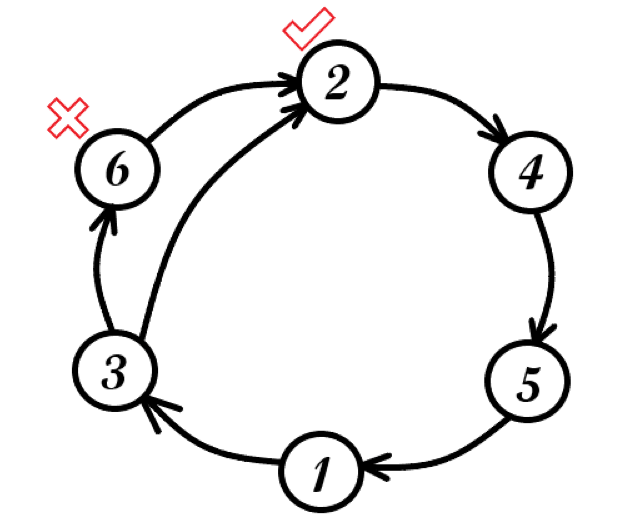
小环和大环可以独立顺时针转动，两个指针 $\color{red}\times$ 和 $\color{red}\surd$ 的位置是固定不动的；当转动小环，视为进行了一次 $\text{multi-drops}$ ，当转动大环，视为进行多次 $\text{Invert}$ 。可以发现，当转动小环，可以将位于小环外的数字，插入任意两个数字之间。在图中，当前 $6$ 位于 $3$ 和 $2$ 之间，转动一次小环， $6$ 就在 $1$ 和 $3$ 之间了；显然，进行一次 $\text{multi-drops}$ ，可以将 $6$ 放入任何你想要的位置。更一般的，若要该边数字 $x$ 在大环中的相对其他数字位置，应该首先用多次 $\text{Invert}$ 将 $x$ 放入 $\color{red}\times$ 标记的位置，然后进行一次 $\text{multi-drops}$ 。我们要对大环上的数字进行排序，那么只需要通过若干次操作，利用小环调整一些数字的相对位置，令大环上形成 $1\to2\to\cdots\to n\to 1\to\cdots$ 这样的环，再进行几次 $\text{Invert}$ 即可将原序列 $p$ 完成排序。
那么问题就变得简单：每次调整一个数的位置就要进行一次 $\text{multi-drops}$ ，因此要调整尽可能少的数字。不妨找出大环上的一个 $\text{LIS}$ （最长上升子序列），其长度为 $len$ ；对于在 $\text{LIS}$ 上的 $len$ 个数字不作调整，只需要调整 $n-len$ 个数字的相对位置；显然，这样的方案使得需要调整的数字个数最小。对于不在 $\text{LIS}$ 上的 $n-len$ 个数字，用 $n-len$ 次 $\text{multi-drops}$ 和若干次 $\text{Invert}$ ，即可将这 $n-len$ 个数字一一放入正确的位置，完成排序。
计算环上的 $\text{LIS}$ 长度时，可以枚举环的起点，对 $n$ 个起点各求一次 $\text{LIS}$ ，取长度最大的即可。时间复杂度为 $O(n^2\log n)$ 。

代码

/******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营（第五场） Problem D
Date: 8/20/2020
Description: Circle, LIS
*******************************************************************/
#include<algorithm>
#include<iostream>
#include<cstdio>
using namespace std;
const int N=504;
int n;
int p[N];
int a[N];
int dp[N];
int main(){
    cin>>n;
    int i,j;
    for(i=1;i<=n;i++){
        scanf("%d",p+i);
    }
    int ans=0x3f3f3f3f;
    //枚举环的起点
    for(i=1;i<=n;i++){
        for(j=1;j<=n;j++){
            //环确定了起点为i
            //于是可以环拉成链
            a[j]=p[i+j-1-n*(i+j-1>n)];
        }
        //求LIS
        int len=1;
        dp[1]=a[1];
        for(j=2;j<=n;j++){
            if(a[j]>dp[len]){
                dp[++len]=a[j];
            }else{
                *lower_bound(dp+1,dp+1+len,a[j])=a[j];
            }
        }
        ans=min(n-len,ans);//最小调整次数
    }
    cout<<ans<<endl;
    return 0;
}