牛客多校第一场总结

1 A Monotonic Matrix

先备知识
LGV 算法 (Lindström–Gessel–Viennot lemma)
求

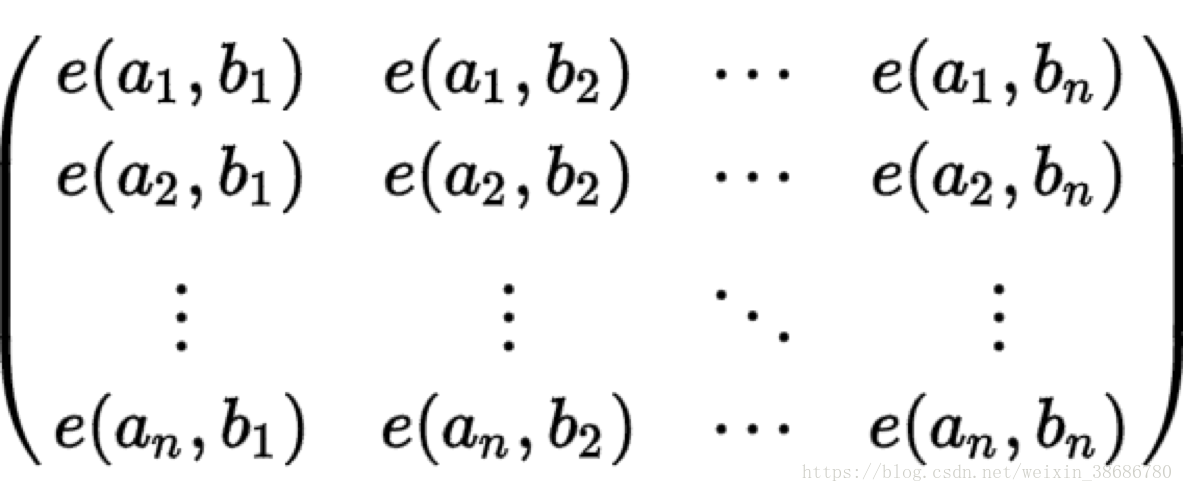
求以上矩阵的行列式，其中 e(a,b) 是a-b的方法数，带入就能求(a1,a2,…an) - (b1,b2,…bn) 的所有不相交路径的种数

考虑01和12的分界线
是(n, 0)到(0，m)的两条不相交（可重合）路径
分界线以及分界线以上的点是一种，分界线下是一种
平移其中一条变成(n-1, -1)到(-1，m-1);
变成(注意下面图片有个m-1写成n-1了,懒癌不想改了)
起点 { a 1 , a 2 } = { ( n , 0 ) , ( n − 1 , − 1 ) } \
终点 { b 1 , b 2 } = { ( 0 , m ) , ( − 1 , m − 1 ) }

做法 2 http://oeis.org/(网络赛）
仔细找规律
原题地址https://codeforces.com/problemset/problem/348/D
关于LGV的博客
https://www.cnblogs.com/jszkc/p/7309468.html
http://www.cnblogs.com/joyouth/p/5607781.html

2 B Symmetric Matrix

把构造的邻接矩阵变成图结构，通过观察规律递推求出公式
把矩阵和图联系起来（双向）
对邻接矩阵以及题目特殊要求的敏感性
http://oeis.org/(网络赛）

  1. 题意
    求满足下面条件的n*n的矩阵的个数

    2.分析
    仔细分析转换成图的邻接矩阵，可知n个点组成若干个环的方案种数
    边界条件
    d p [ 0 ] = 1 , d p [ 1 ] = 0 , d p [ 2 ] = 1

    下面去递推式，dp[n] 表示节点数为n时的方案数
  2. 前n-1个球取出来一个和第n个球组成一个环
    ( n − 1 ) ∗ d p [ n − 2 ]
  3. 前n-1个球取出来k个，剩下的n-k-1个旧求和第n个球组成一个环
    <munderover> ∑ i = 0 i < n − 2 </munderover> C ( n − 1 , k ) ∗ ( n − k − 1 ) ! / 2 ∗ d p [ i ]

    其中(n-k-i)个旧球 和一个新球组成环的种类的个数是(n-k-1)!,除以2是要去除对称

d p [ n ] = ( n − 1 ) ∗ d p [ n − 2 ] + <munderover> ∑ i = 0 i < n − 2 </munderover> C ( n − 1 , k ) ∗ ( n − k − 1 ) ! / 2 ∗ d p [ i ]

d p [ n ] = ( n − 1 ) ∗ d p [ n − 2 ] + <munderover> ∑ i = 0 i < n − 2 </munderover> ( n − 1 ) ! / k ! / 2 ∗ d p [ i ]

化简得
d p [ n ] = ( n − 1 ) ∗ d p [ n − 2 ] + ( n − 1 ) ∗ ( n − 2 ) / 2 ∗ d p [ n − 3 ] + ( n − 1 ) ∗ ( d p [ n − 1 ] − ( n − 2 ) ∗ d p [ n − 3 ] )
  1. 参考代码
             B.cpp

3 C Fluorescent 2

1 概率论期望的求解
题意： 有m个灯，n个开关，每一个开关都可以控制多个灯反转
用一个n*m ( C i j ) 的矩阵表示,这n个开关可以选择选或者不选，2^n种方法
用f(S) 表示用S这种方法最后灯还亮着的的个数
求

s u m ( f ( S ) 3 )

分析: 用 x i 表示i这个灯最后的状态
那么
f ( S ) 3 = ( x 0 + x 1 + . . . x n − 1 ) 3 = ∑ x i ∗ x j ∗ x j

s u m ( f ( S ) 3 ) = s u m ( ∑ x i ∗ x j ∗ x j ) = E ( ∑ x i ∗ x j ∗ x j ) ∗ 2 n = ∑ P ( x i ∗ x j ∗ x j == 1 ) ∗ 2 n

所以问题转变成了求任意 x i , x j , x k ，最后都亮着的概率和。
也即对于n*m矩阵的每一个列，任意选三个列，每一列异或和都为零的概率和。
根据线性代数秩的定义，先求出这个n*3矩阵的秩r，那么最后 x i ∗ x j ∗ x k 为1的概率就为 1 / 2 r ,这一点不好理解。先选出r个基向量，那么对于剩下的n-r个向量选或者不选，者r个基向量都可以选出一些和这些相同，即可由基向量组合成剩下的n-r个向量的异或和，那么总的异或就是0，符合条件。所以种类是 2 n − r ，概率 2 n − r / 2 n = 1 / 2 r
所以我们求出秩为0，1,3,4的个数，最后求和。
2. 参考代码 C.cpp

4. D Two Graphs

  • 看清楚数据范围
  • 根据榜单判断当前思路是否有问题，是否有更简单或者暴力试一发
  • 遇到新的概念不要慌，仔细审题
  • ————————
    1. 具体思路:
      暴力枚举所有可能的 ϕ ( ) 函数的所有情况 n ! 种情况，然后判断每一种情况是否能和G2图吻合，最重要的排除G1的自同构
  1. 参考代码 D.cpp

5 E Romovel

  1. 字符串删减，字符串匹配与动态规划

6 F Sum of Maximum

1 什么是拉格朗日多项式
大神博客
我的总结拉格朗日多项式及其应用
2 拉格朗日模板+ 本题代码

参考代码 F.cpp

7 G Dreyfus-Wagner

8 H

  1. 求最长路，向下求 down 和向上求 up 操作
  2. 斜率优化

9 I

后缀数组
题意：求一个字符串求所有不同构子串的个数，字符串仅有a,b,c
分析：比较本题与上一题，发现多了一个同构的限制，本字符串内的子串可能有同构的情况，首先想到的方法是除去同构，发现比较难实现，反其道而行之，枚举所有的同构情况，然后除以同构函数的个数6，就可以求出答案，注意特判单个字符的同构。

参考代码 I.cpp

10J

  1. 题意：
    求1-l,r-n这连个段中间不同数的个数

  2. 分析：
    树状数组的运用:将数组加倍,然后求区间(r,l+n)不同数

  3. 参考代码 I.cpp

参考代码 J.cpp