题目难度: 中等
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
存在一个 无向图 ,图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。
给定一个二维数组 graph ,表示图,其中 graph[u] 是一个节点数组,由节点 u 的邻接节点组成。形式上,对于 graph[u] 中的每个 v ,都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性:
- 不存在自环(graph[u] 不包含 u)。
- 不存在平行边(graph[u] 不包含重复值)。
- 如果 v 在 graph[u] 内,那么 u 也应该在 graph[v] 内(该图是无向图)
- 这个图可能不是连通图,也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图 定义:如果能将一个图的节点集合分割成两个独立的子集 A 和 B ,并使图中的每一条边的两个节点一个来自 A 集合,一个来自 B 集合,就将这个图称为 二分图 。
如果图是二分图,返回 true ;否则,返回 false 。
示例 1:
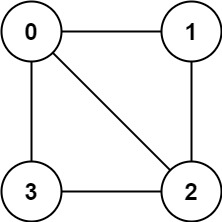
- 输入:graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
- 输出:false
- 解释:不能将节点分割成两个独立的子集,以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。
示例 2:

- 输入:graph = [[1,3],[0,2],[1,3],[0,2]]
- 输出:true
- 解释:可以将节点分成两组: {0, 2} 和 {1, 3} 。
提示:
- graph.length == n
- 1 <= n <= 100
- 0 <= graph[u].length < n
- 0 <= graph[u][i] <= n - 1
- graph[u] 不会包含 u
- graph[u] 的所有值 互不相同
- 如果 graph[u] 包含 v,那么 graph[v] 也会包含 u
题目思考
- 使用什么方法可以判断一条边的两个节点各自属于哪个集合?
解决方案
- 分析题目, 要想判断一条边的两个节点所属的集合, 我们可以采取下面的过程:
- 从任意一个节点 x 出发, 将其放入集合 A 中
- 然后从它开始遍历所有相邻的节点(y1,y2,y3...), 将它们放到集合 B 中
- 然后从所有这些相邻节点(y1,y2,y3...)开始, 继续遍历它们相邻的节点
- 假设现在遍历到了 y1, 它的相邻节点有 z1,z2 和 z3, 此时有以下三种情况:
- a. 假设相邻节点 z1 尚未被添加到集合, 则添加到集合 A, 后面可以从 z1 开始继续遍历相邻
- b. 假设相邻节点 z2 已经被添加到集合 A, 则说明它已经被遍历过且有效, 直接跳过它
- c. 假设相邻节点 z3 已经被添加到集合 B, 则 y1 和 z3 有边相连, 但属于相同集合, 不可能是二分图, 直接返回 false
- 继续上述过程, 直到 x 连通的所有节点都被遍历过, 此时 x 所在的连通分量就是二分图
- 然后我们继续处理图中的其他尚未遍历的节点, 直到所有节点都被遍历为止
- 如果在整个遍历过程中都没有提前返回 false, 则说明整个图都是二分图, 返回 true
- 具体代码实现时, 我们可以使用一个颜色字典来模拟集合, 如果一个节点对应的值是 0, 则位于集合 A, 如果是 1 则位于集合 B, 这就是经典的染色法
- 然后遍历 0~n-1 的节点, 如果当前节点不在字典中, 则说明它尚未被遍历, 以它为起点应用上面的流程, 这里可以用 BFS 或者 DFS 实现
- 下面的代码采用了 BFS, 并对必要步骤有详细的解释, 方便大家理解
复杂度
- 时间复杂度
O(N): N 是节点数目, 每个节点都只用染一遍颜色 - 空间复杂度
O(N): 使用了一个字典存储每个节点被染上的颜色
代码
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
### 染色法+BFS
# 颜色字典, 存储每个节点被染上的颜色
color = {}
for node in range(len(graph)):
if node not in color:
# 当前节点尚未被染色, 开始BFS
q = [node]
# 初始化该节点颜色为0
color[node] = 0
for cur in q:
for nex in graph[cur]:
# 遍历相邻节点
if nex not in color:
# 如果相邻节点尚未染色, 则染上和当前节点不同的颜色
color[nex] = 1 - color[cur]
# 然后将其加入队列中, 等待后续处理
q.append(nex)
elif color[nex] == color[cur]:
# 相邻节点已经被染上了和当前节点相同的颜色, 不可能是二分图, 直接返回false
return False
# 所有节点都被成功染色, 且保证了相邻节点颜色一定不同, 是有效的二分图
return True
大家可以在下面这些地方找到我~😊
我的公众号: 算法精选, 欢迎大家扫码关注~😊





 京公网安备 11010502036488号
京公网安备 11010502036488号