基础数据结构——1.4二叉树和堆(一)1
1.4.1 二叉树的基本概念2
树的基本概念
树是一种特殊的图,其是由 个结点, 条边连接而构成的连通图.
如下图1.4.1所示,图中的圆代表结点,线段代表边,结点中的字母是为了方便描述结点而设置的结点的编号.
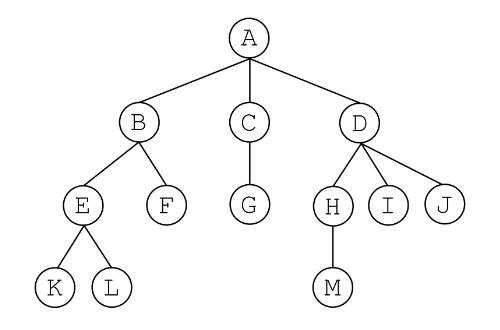
- 根结点(root):为了方便描述树,人为规定树中的某个结点为根结点.
- 父结点:在规定根结点后,除根结点外,每个结点都会有唯一的父结点.
- 子结点:若点 是点 的父结点,则称点 是点 的子结点.
- 根结点没有父结点.
- 与根结点直接相连的结点,它们的父结点都是根结点.
- 对于点 ,除了其父结点外,其他与点 直接相连的结点都是点 的子结点.
- 叶子结点:若点 没有子结点,则点 为叶子结点.
- 子树:规定根结点后,点 往下的部分也是一棵树,称为以点 为根结点的子树.
- 深度/层数(depth):若设根结点的深度 ,则从根结点开始,若点 是点 的子结点,则有 .
例如,如上图1.4.1所示,若设根结点为点 ,则:
- 点 是点 的父结点,点 是点 的子结点,且点 是叶子结点.
- 以点 为根结点的子树中的点有 .
- .
二叉树的基本概念
二叉树是一种特殊的树,其一定有根节点,并且每个结点至多有两个子结点,分别称为左子结点和右子结点,以左子结点为根的子树称为左子树,以右子结点为根的子树称为右子树.
如下图1.4.2所示,为一棵二叉树.
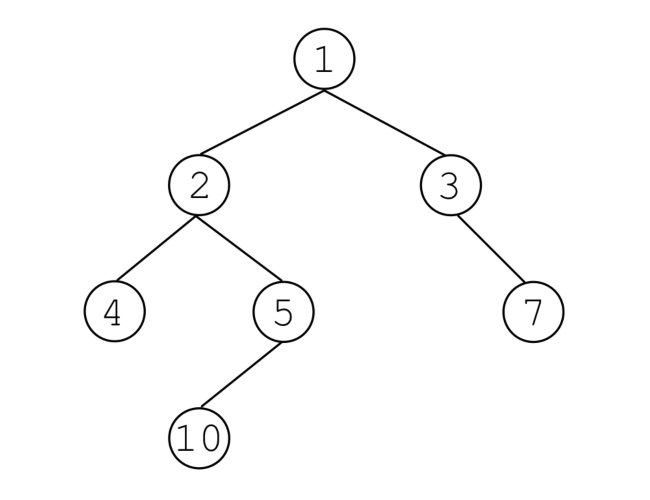
对于一棵层数最大为 的二叉树来说:
- 满二叉树:若除叶子结点外所有结点都有 个子结点,则称之为满二叉树.
- 二叉树的第 层(所有 的结点都在第 层)至多有 个结点,故满二叉树总共有 个结点.
- 完全二叉树:若只有第 层的最后几个结点缺失,则称之为完全二叉树.
- 对于一棵有 个结点的完全二叉树来说,其层数最多为 .
如下图1.4.3所示,图左为一棵满二叉树,图右为一棵完全二叉树.
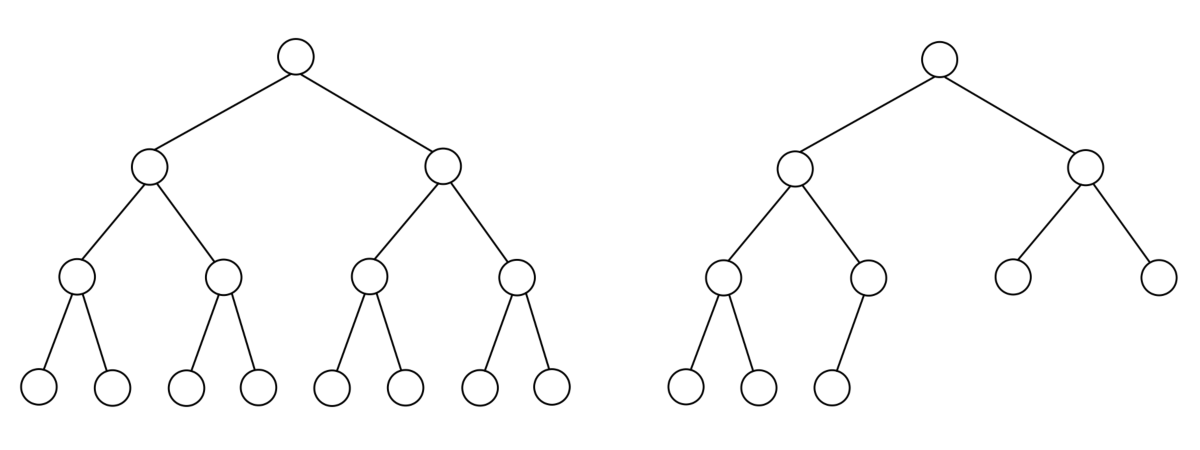
二叉树的存储
第一种存储方式是使用结构体或数组,存储编号为 的结点的左子结点和右子结点的编号.
有如下代码片段:
//代码片段-二叉树的结构体存储
struct Node {
int val, l, r;
} tr[N];
/*
二叉树的结点可能有点权,这里点权设为 val
对于二叉树的第 i 个结点 tr[i] 来说,其左子结点为 tr[i].l,其右子结点为 tr[i].r
*/
第二种存储方式,则是利用二叉树的结构特点.
设二叉树的根结点编号为 ,则有:
- 对于编号为 的结点,其左子结点的编号为 ,右子结点的编号为 .
- 对于编号为 的结点,其父结点的编号为 .
如此存储二叉树,结点编号互不冲突,但编号不一定连续.
若根结点编号为 ,则有:
- 对于编号为 的结点,其左子结点的编号为 ,右子结点的编号为 .
- 对于编号为 的结点,其父结点的编号为 .
二叉树的遍历
先序遍历
从二叉树的根结点开始,由如下规则打印出的序列为先序遍历序列,此遍历二叉树的方法为先序遍历:
- 打印当前结点的编号.
- 若当前结点有左子结点,则访问左子结点,访问后回到当前结点.
- 若当前结点有右子结点,则访问右子结点,访问后回到当前结点.
- 退出当前结点.
根据先序遍历的打印顺序,有口诀根左右.
有如下代码片段:
//代码片段-先序遍历
void PreOrder(int x) {
printf("%d ", x);
if (tr[x].l) PreOrder(tr[x].l);
if (tr[x].r) PreOrder(tr[x].r);
}
对于先序遍历序列来说,序列的第一个数即为二叉树根结点的编号.
中序遍历
从二叉树的根结点开始,由如下规则打印出的序列为中序遍历序列,此遍历二叉树的方法为中序遍历:
- 若当前结点有左子结点,则访问左子结点,访问后回到当前结点.
- 打印当前结点的编号.
- 若当前结点有右子结点,则访问右子结点,访问后回到当前结点.
- 退出当前结点.
根据中序遍历的打印顺序,有口诀左根右.
有如下代码片段:
//代码片段-中序遍历
void InOrder(int x) {
if (tr[x].l) PreOrder(tr[x].l);
printf("%d ", x);
if (tr[x].r) PreOrder(tr[x].r);
}
对于长度为 的中序遍历序列来说,若根结点为序列的第 个数,则
- 序列的 为二叉树根结点的左子树.
- 序列的 为二叉树根结点的
后序遍历
从二叉树的根结点开始,由如下规则打印出的序列为后序遍历序列,此遍历二叉树的方法为后序遍历:
- 若当前结点有左子结点,则访问左子结点,访问后回到当前结点.
- 若当前结点有右子结点,则访问右子结点,访问后回到当前结点.
- 打印当前结点的编号.
- 退出当前结点.
根据后序遍历的打印顺序,有口诀左右根.
有如下代码片段:
//代码片段-后序遍历
void PostOrder(int x) {
if (tr[x].l) PreOrder(tr[x].l);
if (tr[x].r) PreOrder(tr[x].r);
printf("%d ", x);
}
对于后序遍历序列来说,序列的最后一个数即为二叉树根结点的编号.
层序遍历
若一棵二叉树最多有 层,则从二叉树的第 层(只有一个根结点)开始,依次打印每层的结点编号,所得的序列为层序遍历序列.
有如下代码片段:
//代码片段-层序遍历
void DepthOrder(int x) {
if (depth_order.size() <= depth[x]) depth_order.push_back({x});
else depth_order[depth[x]].push_back(x);
if (tr[x].l) PreOrder(tr[x].l);
if (tr[x].r) PreOrder(tr[x].r);
}
void DepthOrderPrint() {
for (int i = 1; i < depth_order.size(); ++i)
for (auto &x : depth_order[i])
cout << x << ' ';
}
层序遍历序列还有其他方法得到,这个方法将在广度优先搜索BFS中介绍.
对于一棵二叉树来说:
- 若得知了中序遍历的情况下,再得知先序遍历或后序遍历的其中一种,就可以还原整棵二叉树.
- 若没有得到中序遍历,只知道先序遍历和后序遍历,则不一定能还原二叉树.
二叉树 习题
洛谷 P1305 新二叉树
时间限制:1.00s 内存限制:125.00MB题目描述
输入一串二叉树,输出其前序遍历。
输入格式
第一行为二叉树的节点数 。()
后面 行,每一个字母为节点,后两个字母分别为其左右儿子。特别地,数据保证第一行读入的节点必为根节点。
空节点用
*表示输出格式
二叉树的前序遍历。
样例输入
6 abc bdi cj* d** i** j**样例输出
abdicj
题解
按照结构体存储方法存储二叉树,之后进行先序遍历即可.
代码实现
注意这里的点的编号为字母,存储结点时需要进行处理.
如下为结构体存储二叉树的参考代码.
//洛谷P1305新二叉树
#include<bits/stdc++.h>
using namespace std;
const int N = 27;
struct Node {
int l, r;
} tr[N];
void PreOrder(char x) {
if (x + 'a' == '*') return;
cout << char(x + 'a');
PreOrder(tr[x].l);
PreOrder(tr[x].r);
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int n, ROOT; cin >> n;
for (int i = 1; i <= n; ++i) {
char root, lson, rson;
cin >> root >> lson >> rson;
tr[root - 'a'].l = lson - 'a';
tr[root - 'a'].r = rson - 'a';
if (i == 1) ROOT = root - 'a';
}
PreOrder(ROOT);
return 0;
}
时间复杂度分析
以时间复杂度为 .
洛谷 P1030 [NOIP2001 普及组] 求先序排列
时间限制:1.00s 内存限制:125.00MB题目描述
给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数 )。
输入格式
共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。
输出格式
共一行一个字符串,表示一棵二叉树的先序。
样例输入
BADC BDCA样例输出
ABCD题目来源
NOIP 2001 普及组第三题
题解
对于当前的中序遍历 和后序遍历 ,有:
-
后序遍历 的最后一个元素 即为当前子树的根结点.
-
在中序遍历 中找到该元素 ,则
-
为中序遍历中,当前子树的左子树,左子树大小为 .
-
为中序遍历中,当前子树的右子树.
-
为后序遍历中,当前子树的左子树.
-
为后序遍历中,当前子树的右子树.
-
按照先序遍历,先打印根结点,再遍历左子树,再遍历右子树即可.
代码实现
在代码实现时,不需要还原整个二叉树,只需要关心当前子树的根结点即可.
如下为参考代码.
//洛谷P1030求先序排列
#include<bits/stdc++.h>
using namespace std;
string InOrder, PostOrder;
void PreOrder(int In_L, int In_R, int Post_L, int Post_R) {
if (In_L > In_R) return; // 越界返回
int root = PostOrder[Post_R]; // 当前子树的根结点为 后序遍历 的最后一个元素
cout << PostOrder[Post_R]; // 打印根结点
int x = In_L;
while (InOrder[x] != root) ++x; // 在中序遍历中找到该根结点
int L_size = x - In_L;
PreOrder(In_L, x - 1, Post_L, Post_L + L_size - 1); // 遍历左子树
PreOrder(x + 1, In_R, Post_L + L_size, Post_R - 1); // 遍历右子树
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> InOrder >> PostOrder;
int n = InOrder.size();
PreOrder(0, n - 1, 0, n - 1);
return 0;
}
时间复杂度分析
考虑最坏情况,每个结点只有一棵子树,则每次只能去掉一个结点,考虑到还需要遍历一遍序列,最坏时间复杂度为 .
洛谷 P1229 遍历问题
时间限制:1.00s 内存限制:125.00MB题目描述
我们都很熟悉二叉树的前序、中序、后序遍历,在数据结构中常提出这样的问题:已知一棵二叉树的前序和中序遍历,求它的后序遍历,相应的,已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序遍历,你却不能确定其中序遍历序列,考虑如下图中的几棵二叉树:
所有这些二叉树都有着相同的前序遍历和后序遍历,但中序遍历却不相同。
输入格式
输入数据共两行,第一行表示该二叉树的前序遍历结果s1,第二行表示该二叉树的后序遍历结果s2。
输出格式
输出可能的中序遍历序列的总数,结果不超过长整型数。
样例输入
abc cba样例输出
4
题解
当某个结点只有一棵子树时,则这棵子树就不能确定是左子树还是右子树,故在中序遍历中,此子树范围内的所有元素,既可能在中序遍历的当前结点的左侧,也可能在当前结点的右侧.
一开始,假设只有一种中序遍历,即 .
对于当前先序遍历 和后序遍历 来说:
- ,即先序遍历的第一个结点和后序遍历的最后一个结点相同,为当前子树的根结点.
- 若当前结点的左子树存在,则其左子树的根结点为 .
- 在后序遍历中找到该结点 ,有
- 为后序遍历中,当前结点的左子树,左子树大小为 .
- 为后序遍历中,当前结点的右子树.
- 为先序遍历中,当前结点的左子树.
- 为先序遍历中,当前结点的右子树.
- 若 ,则说明当前结点没有右子树,换句话说,就是只有一棵子树,则让 .
遍历结束后输出 即可.
代码实现
如下为参考代码.
//洛谷P1229遍历问题
#include<bits/stdc++.h>
using namespace std;
int ans = 1;
string PreOrder, PostOrder;
void calc(int L_Pre, int R_Pre, int L_Post, int R_Post) {
if (L_Pre >= R_Pre) return; // 若只剩下一个结点,则其没有左右子树了,也需要返回
int L_root = PreOrder[L_Pre + 1];
int x = L_Post;
while (PostOrder[x] != L_root) ++x;
int L_size = x - L_Post + 1;
if (L_size == R_Pre - L_Pre) ans *= 2;
calc(L_Pre + 1, L_Pre + L_size, L_Post, x);
calc(L_Pre + L_size + 1, R_Pre, x + 1, R_Post - 1);
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> PreOrder >> PostOrder;
int n = PreOrder.size();
calc(0, n - 1, 0, n - 1);
cout << ans;
return 0;
}
时间复杂度分析
考虑最坏情况,每个结点只有一棵子树,则每次只能去掉一个结点,考虑到还需要遍历一遍序列,最坏时间复杂度为 .
洛谷 P1087 [NOIP2004 普及组] FBI 树
时间限制:1.00s 内存限制:125.00MB题目描述
我们可以把由 0 和 1 组成的字符串分为三类:全 0 串称为 B 串,全 1 串称为 I 串,既含 0 又含 1 的串则称为 F 串。
FBI 树是一种二叉树,它的结点类型也包括 F 结点,B 结点和 I 结点三种。由一个长度为 的 01 串 可以构造出一棵 FBI 树 ,递归的构造方法如下:
- 的根结点为 ,其类型与串 的类型相同;
- 若串 的长度大于 ,将串 从中间分开,分为等长的左右子串 和 ;由左子串 构造 的左子树 ,由右子串 构造 的右子树 。
现在给定一个长度为 的 01 串,请用上述构造方法构造出一棵 FBI 树,并输出它的后序遍历序列。
输入格式
第一行是一个整数 ,
第二行是一个长度为 的 01 串。
输出格式
一个字符串,即 FBI 树的后序遍历序列。
样例输入
3 10001011样例输出 #1
IBFBBBFIBFIIIFF提示
对于 的数据,;
对于全部的数据,。
noip2004普及组第3题
题解
如下图1.4.4所示,为样例按照题意说明构造出的 FBI 树.
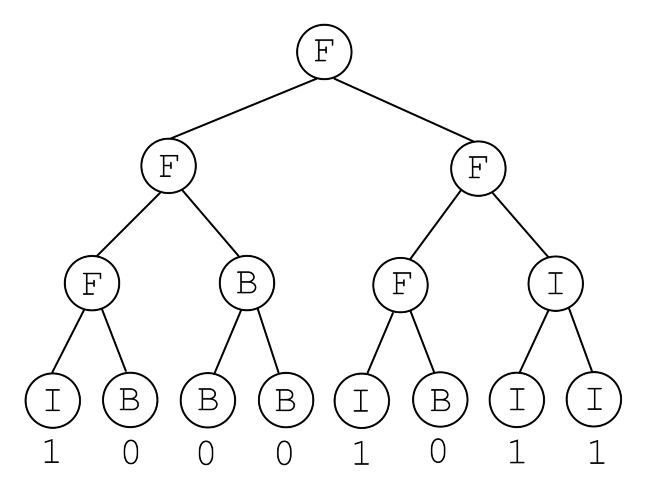
即对于当前区间 ,若:
- ,则即可根据 来确定叶子结点上的字符串.
- 否则的话,则根据左右子结点上的字符即可确定当前结点上的字符.
- 设当前结点上的字符为 ,左子结点上的字符为 ,右子结点上的字符为 .
- 若 ,有 ,否则有 .
这样 FBI 树就构造好了,进行后序遍历即可.
代码实现
//洛谷 P1087 FBI树
#include<bits/stdc++.h>
using namespace std;
const int N = (1 << 10) + 1;
string s;
char build_tree(int l, int r) {
char ch;
if (l == r) {
if (s[l - 1] == '0') ch = 'B';
else ch = 'I';
cout << ch;
return ch;
}
int mid = l + r >> 1;
char ch_L = build_tree(l, mid);
char ch_R = build_tree(mid + 1, r);
if (ch_L != ch_R) ch = 'F';
else ch = ch_L;
cout << ch;
return ch;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int n; cin >> n; n = (1 << n);
cin >> s;
build_tree(1, n);
return 0;
}
时间复杂度分析
想要到达叶子结点,则需要每次都对当前区间除以 ,需要进行 次除法才能到达叶子结点.
所以总的时间复杂度为 .
洛谷 P5597 【XR-4】复读
时间限制:1.00s 内存限制:500.00MB题目背景
赛时提醒:当机器人在这棵完全二叉树的根时,执行
U是非法的,即你需要保证不可能出现这种情况。赛时提醒:这棵二叉树是无限向下延伸的,即所有节点均有左子节点与右子节点,除了根的所有节点均有父亲。
题目描述
小 X 捡到了一台复读机,这台复读机可以向机器人发号施令。机器人将站在一棵完全二叉树的根上,完全二叉树是无限延伸的。你将向复读机录入一串指令,这串指令单个字符可以是:
L:命令机器人向当前节点的左子走;R:命令机器人向当前节点的右子走;U:命令机器人向当前节点的父亲走(若没有,则命令非法)。录入指令后,复读机将会把指令无限复读下去。比如命令为
LR,那么机器人会遵从LRLRLRLR...一直走下去。这棵完全二叉树上有一个 个节点的连通块,保证这个连通块包含根节点。连通块上的每个节点都埋有宝藏,机器人到达过的地方如果有宝藏,则会将其开采。如果一个地方没有宝藏,机器人也可以到那里去。机器人也可以反复经过一个地方。
显然,这个连通块本身也是一棵二叉树。
现在,有人告诉了小 X 埋有宝藏的这棵二叉树的前序遍历,小 X 需要寻找到一条尽量短的指令,使得机器人能够挖掘出所有宝藏。
输入格式
一行一个字符串,由
0123中的字符组成,表示埋有宝藏的这棵二叉树的前序遍历。
0:表示这是一个没有儿子的节点。1:表示这是一个只有左子的节点。2:表示这是一个只有右子的节点。3:表示这是一个既有左子又有右子的节点。输出格式
一个整数,表示最短指令的长度。
样例输入 #1
1313000样例输出 #1
3样例输入 #2
333003003300300样例输出 #2
15提示
【样例 1 说明】
一种可行的最短指令为
LRU。
本题采用捆绑测试。
- Subtask 1(31 points):。
- Subtask 2(32 points):。
- Subtask 3(37 points):无特殊限制。
对于 的数据,。
题解3
首先,对于一个合格的指令,有:
- 其出发点和结束点的相对位置应该是不变的(作为叶子结点的结束点可能会提前到达).
- 执行指令不会回到出发点和其往上的部分.
那么从根结点出发,根据出发点和结束点的位置,可以划分出几棵子树,将这些子树的根结点对齐后,可以得到一棵新的树,这里命名为指令树.
如下图1.4.5所示,左图为原本的树 ,右图为左图的一棵指令树 .
左图原本的树上的红色结点为出发点和结束点,这样整棵树被划分为了两棵子树,分别用橙色和蓝色表示.
右图指令树则是让两树的根结点对齐产生的新树,紫色部分为两棵子树重叠的部分.
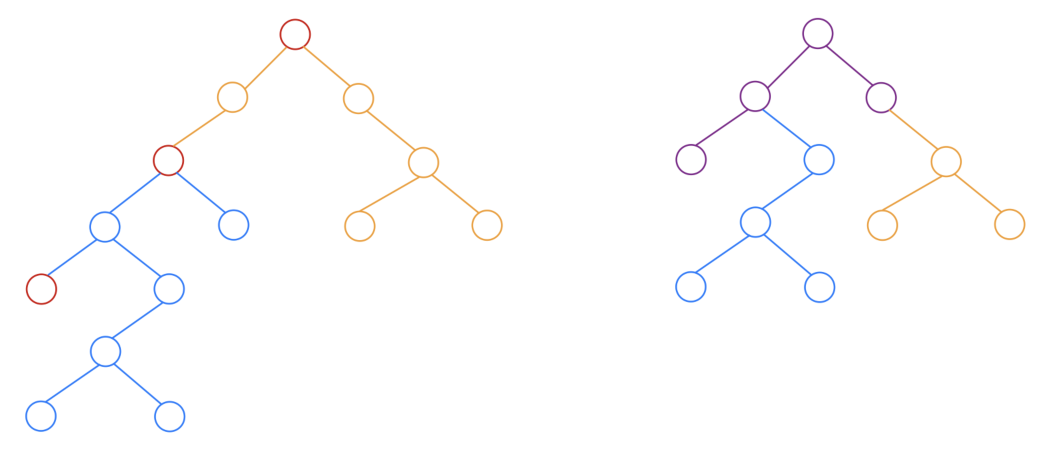
若指令树 的所有结点数量为 ,出发点到结束点的路径长度为 ,则这种指令的最短长度为 .
这里的出发点到结束点的路径长度可以理解为:从结束点开始不断走向父结点,一定能走回出发点,这一段路径走过的边数即为路径长度.
除了指令树的根结点外,其他每个结点都有唯一向父结点走的边,一共有 条.
若默认回到指令树的根结点,则需要走的边数为 .
但需要从指令树的根结点走到结束点,所以需要再减去这一段路径的边数,即 .
最终指令的最短长度为 .
所以可以通过枚举原本的树上的结束点,来确定所有种类的指令中,最短的指令长度即可.
代码实现
//洛谷P5597复读
#include<bits/stdc++.h>
using namespace std;
const int N = 2005;
string s;
int idx, root, tmp_root, tr_size, tmp_tr_size, path[N], ans = INT_MAX;
struct Node {
int l, r;
} tr[N], tmp_tr[N];
void build_tree(int &x) {
x = ++tr_size;
char ch = s[idx++];
if (ch == '1' || ch == '3') build_tree(tr[x].l);
if (ch == '2' || ch == '3') build_tree(tr[x].r);
}
void merge_tree(int &x, int u, int v) {
if (!x) x = ++tmp_tr_size;
if (u == v) return;
if (tr[u].l) merge_tree(tmp_tr[x].l, tr[u].l, v);
if (tr[u].r) merge_tree(tmp_tr[x].r, tr[u].r, v);
}
void calc(int u, int len) {
if (u != root) {
memset(tmp_tr, 0, sizeof(tmp_tr)); tmp_tr_size = 0; tmp_root = 0;
int tmp_u = root;
while (tmp_u) {
int tmp_v = tmp_u;
for (int i = 0; i < len; ++i) tmp_v = (path[i] == 0 ? tr[tmp_v].l : tr[tmp_v].r);
merge_tree(tmp_root, tmp_u, tmp_v);
tmp_u = tmp_v;
}
ans = min(ans, (tmp_tr_size - 1) * 2 - len);
}
if (tr[u].l) {
path[len] = 0;
calc(tr[u].l, len + 1);
}
if (tr[u].r) {
path[len] = 1;
calc(tr[u].r, len + 1);
}
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> s;
build_tree(root);
calc(root, 0);
cout << ans;
return 0;
}
时间复杂度分析
枚举结束点的时间是 ,在结束点确定的情况下划分原本的树的时间也是 的.
所以总的时间复杂度为 .
以下题目的解法已经在本节介绍过(或过于相似)
以下题目会在后继章节补充.



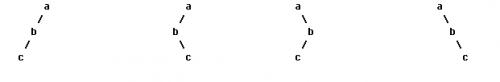


 京公网安备 11010502036488号
京公网安备 11010502036488号