目标函数
Lasso相当于带有L1正则化项的线性回归。先看下目标函数: RSS(w)+λ∥w∥1=∑i=0N(yi−∑j=0Dwjhj(xi))2+λ∑j=0D∣wj∣
这个问题由于正则化项在零点处不可求导,所以使用非梯度下降法进行求解,如坐标下降法或最小角回归法。
坐标下降法
本文介绍坐标下降法。
坐标下降算法每次选择一个维度进行参数更新,维度的选择可以是随机的或者是按顺序。
当一轮更新结束后,更新步长的最大值少于预设阈值时,终止迭代。
下面分为两部求解
RSS偏导
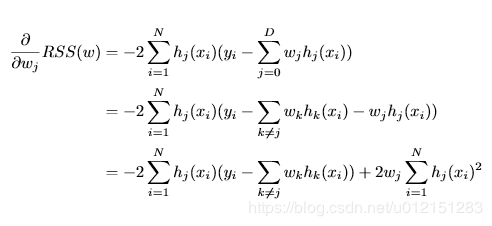
下面做一下标记化简
ρj=∑i=1Nhj(xi)(yi−∑k̸=jwkhk(xi))
zj=∑i=1Nhj(xi)2
上式化简为 ∂wj∂RSS(w)=−2ρj+2wjzj
正则项偏导
次梯度方法(subgradient method)是传统的梯度下降方法的拓展,用来处理不可导的凸函数。

λ∂wj∣wj∣=⎩⎪⎨⎪⎧−λ[−λ,λ]λwj<0wj=0wj>0
整体偏导数
λ∂wj[lasso cost]=2zjwj−2ρj+⎩⎪⎨⎪⎧−λ[−λ,λ]λwj<0wj=0wj>0=⎩⎪⎨⎪⎧2zjwj−2ρj−λ[−2ρj−λ,−2ρj+λ]2zjwj−2ρj+λwj<0wj=0wj>0
要想获得最有解,令
λ∂wj[lasso cost]=0。
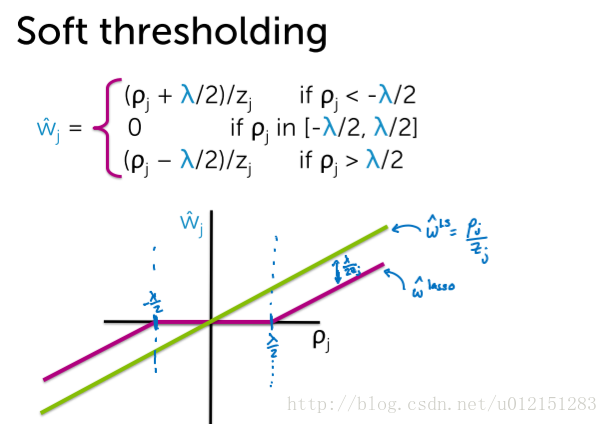
解得,
w^j=⎩⎪⎨⎪⎧(ρj+λ/2)/zj0(ρj−λ/2)/zjρj<−λ/2ρj in [−λ/2,λ/2]ρj>λ/2
伪代码
预计算 zj=∑i=1Nhj(xi)2
初始化参数w(全0或随机)
循环直到收敛:
for j = 0,1,…D
$ \space \space\space\space\rho_j=\sum_{i=1}^Nh_j(x_i)(y_i-\sum_{k \neq j }w_kh_k(x_i))$
update wj
选择变化幅度最大的维度进行更新
概率解释
拉普拉斯分布
随机变量 X∼Laplace(μ,b),其中 μ是位置参数, b>0是尺度参数。
概率密度函数为
f(x∣μ,b)=2b1exp(−b∣x−μ∣)
MAP推导
假设 ϵi∼N(0,σ2), wi∼Laplace(0,λ1)

等价于




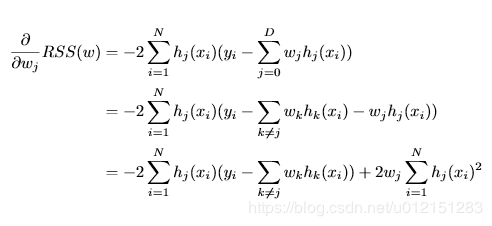





 京公网安备 11010502036488号
京公网安备 11010502036488号