描述
题目描述
给我们一个二叉搜索树,然后我们转换为有序的链表结构
首先明确这么几个概念:
- 二叉搜索树: 左子树上的所有节点的值均小于它的根节点的值, 右子树上所有节点的值均大于他的根节点的值
- 中序遍历: 首先遍历左子树, 再遍历根节点, 最后遍历右节点
- 这里我们中序遍历的顺序恰好就是我们排序后的链表中的节点顺序
这里讲述一下中序遍历的顺序
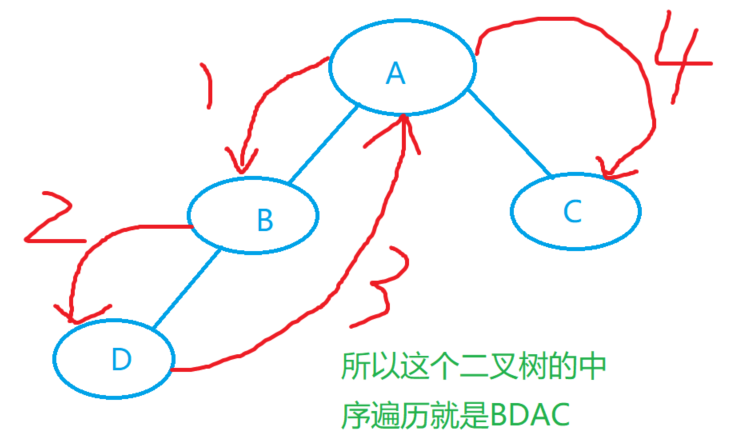
题解
解法一: 直接暴力存储
实现思路
既然我们二叉搜索树的中序遍历恰好就是我们最后的答案, 那么我们可以直接暴力把我们的结果都先放入一个数组中, 然后我们直接对这个数组里面的节点重新确立顺序就完成了
代码实现
class Solution {
vector<TreeNode*> res;
public:
void dfs(TreeNode* root) {
if (root == nullptr) return;
dfs(root->left);
res.emplace_back(root);
dfs(root->right);
}
// 这个是我们中序遍历的模板
TreeNode* Convert(TreeNode* pRootOfTree) {
if (pRootOfTree == nullptr) return pRootOfTree;
dfs(pRootOfTree);
for (int i = 0; i < res.size() - 1; i++)
res[i]->right = res[i + 1], res[i + 1]->left = res[i];
// 我们对我们的所有节点,作为一个链表去确定他们的左右节点
return res[0];
}
};
时空复杂度分析
时间复杂度:
理由如下: 我们中序遍历的时间复杂度就是, 同时我们遍历我们最后的所有的节点的时间复杂度也是
空间复杂度:
理由如下: 我们存入了所有的节点
解法二: 不增加新的空间
实现思路
这里我们可以直接在中序遍历的时候构建我们的链表, 我们可以这么想, 首先当我们的节点为空的时候, 代表到达了叶子节点的下一层, 我们直接返回, 然后我们构建链表的话, 如果为空, 代表访问的是链表的头节点, 不为空的时候, 我们就要考虑他的左右, 然后我们每次保存我们的
代码实现
class Solution {
TreeNode *pre, *res;
public:
void dfs(TreeNode* root) {
if (root == nullptr) return;
dfs(root->left);
pre == nullptr ? res = root : pre->right = root;
// pre记录双向链表中位于root左侧的节点, 如果pre不为空,cur左侧存在节点pre,所以把pre的右节点更新为root
root->left = pre, pre = root;
// pre是否为空对我们的root->left = pre无影响, 然后让pre指向当前的root
dfs(root->right);
}
// 这个是我们中序遍历的模板
TreeNode* Convert(TreeNode* pRootOfTree) {
if (pRootOfTree == nullptr) return pRootOfTree;
dfs(pRootOfTree);
return res;
}
};
时空复杂度分析
时间复杂度:
理由如下: 中序遍历的时间复杂度
空间复杂度:
理由如下: 极限情况下退化成链, 系统的递归栈使用的空间就是






 京公网安备 11010502036488号
京公网安备 11010502036488号