第二弹数据结构初步的主要内容有以下几部分:二叉搜索树、队列与优先队列、堆栈Stack、完全二叉树与满二叉树、哈希表。
一、二叉搜索树
1、 二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
(1)、若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
(2)、若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
(3)、它的左、右子树也分别为二叉查找树。
2、二叉查找树的基本运算
- /* bst - binary search/sort tree
- * by Richard Tang <tanglinux@gmail.com>
- */
- #include <stdio.h>
- #include <stdlib.h>
- typedef int data_type;
- typedef struct bst_node {
- data_type data;
- struct bst_node *lchild, *rchild;
- }bst_t, *bst_p;
(1)、插入
在二叉查找树中插入新结点,要保证插入新结点后仍能满足二叉查找树的性质。例子中的插入过程如下:
a、若二叉查找树root为空,则使新结点为根;
b、若二叉查找树root不为空,则通过search_bst_for_insert函数寻找插入点并返回它的地址(若新结点中的关键字已经存在,则返回空指针);
c、若新结点的关键字小于插入点的关键字,则将新结点插入到插入点的左子树中,大于则插入到插入点的右子树中。
- static bst_p search_bst_for_insert(bst_p *root, data_type key)
- {
- bst_p s, p = *root;
- while (p) {
- s = p;
- if (p->data == key)
- return NULL;
- p = (key < p->data) ? p->lchild : p->rchild;
- }
- return s;
- }
- void insert_bst_node(bst_p *root, data_type data)
- {
- bst_p s, p;
- s = malloc(sizeof(struct bst_node));
- if (!s)
- perror("Allocate dynamic memory");
- s -> data = data;
- s -> lchild = s -> rchild = NULL;
- if (*root == NULL)
- *root = s;
- else {
- p = search_bst_for_insert(root, data);
- if (p == NULL) {
- fprintf(stderr, "The %d already exists.\n", data);
- free(s);
- return;
- }
- if (data < p->data)
- p->lchild = s;
- else
- p->rchild = s;
- }
- }
(2)、遍历
- static int print(data_type data)
- {
- printf("%d ", data);
- return 1;
- }
- int pre_order_traverse(bst_p root, int (*visit)(data_type data))
- {
- if (root) {
- if (visit(root->data))
- if (pre_order_traverse(root->lchild, visit))
- if (pre_order_traverse(root->rchild, visit))
- return 1;
- return 0;
- }
- else
- return 1;
- }
- int post_order_traverse(bst_p root, int (*visit)(data_type data))
- {
- if (root) {
- if (post_order_traverse(root->lchild, visit))
- if (visit(root->data))
- if (post_order_traverse(root->rchild, visit))
- return 1;
- return 0;
- }
- else
- return 1;
- }
中序遍历二叉查找树可得到一个关键字的有序序列。
(3)、删除
删除某个结点后依然要保持二叉查找树的特性。例子中的删除过程如下:
a、若删除点是叶子结点,则设置其双亲结点的指针为空。
b、若删除点只有左子树,或只有右子树,则设置其双亲结点的指针指向左子树或右子树。
c、若删除点的左右子树均不为空,则:
1)、查询删除点的右子树的左子树是否为空,若为空,则把删除点的左子树设为删除点的右子树的左子树。

2)、若不为空,则继续查询左子树,直到找到最底层的左子树为止。

- void delete_bst_node(bst_p *root, data_type data)
- {
- bst_p p = *root, parent, s;
- if (!p) {
- fprintf(stderr, "Not found %d.\n", data);
- return;
- }
- if (p->data == data) {
- /* It's a leaf node */
- if (!p->rchild && !p->lchild) {
- *root = NULL;
- free(p);
- }
- /* the right child is NULL */
- else if (!p->rchild) {
- *root = p->lchild;
- free(p);
- }
- /* the left child is NULL */
- else if (!p->lchild) {
- *root = p->rchild;
- free(p);
- }
- /* the node has both children */
- else {
- s = p->rchild;
- /* the s without left child */
- if (!s->lchild)
- s->lchild = p->lchild;
- /* the s have left child */
- else {
- /* find the smallest node in the left subtree of s */
- while (s->lchild) {
- /* record the parent node of s */
- parent = s;
- s = s->lchild;
- }
- parent->lchild = s->rchild;
- s->lchild = p->lchild;
- s->rchild = p->rchild;
- }
- *root = s;
- free(p);
- }
- }
- else if (data > p->data) {
- delete_bst_node(&(p->rchild), data);
- }
- else if (data < p->data) {
- delete_bst_node(&(p->lchild), data);
- }
- }
4、二叉查找树的查找分析
同样的关键字,以不同的插入顺序,会产生不同形态的二叉查找树。
- int main(int argc, char *argv[])
- {
- int i, num;
- bst_p root = NULL;
- if (argc < 2) {
- fprintf(stderr, "Usage: %s num\n", argv[0]);
- exit(-1);
- }
- num = atoi(argv[1]);
- data_type arr[num];
- printf("Please enter %d integers:\n", num);
- for (i = 0; i < num; i++) {
- scanf("%d", &arr[i]);
- insert_bst_node(&root, arr[i]);
- }
- printf("\npre order traverse: ");
- pre_order_traverse(root, print);
- printf("\npost order traverse: ");
- post_order_traverse(root, print);
- printf("\n");
- delete_bst_node(&root, 45);
- printf("\npre order traverse: ");
- pre_order_traverse(root, print);
- printf("\npost order traverse: ");
- post_order_traverse(root, print);
- printf("\n");
- return 0;
- }
运行两次,以不同的顺序输入相同的六个关键字:


根据前序遍历的结果可得到两次运行所产生的二叉查找树的形态并不相同,如下图:

二、队列与优先队列
队列:
队列特性:先进先出(FIFO)——先进队列的元素先出队列。来源于我们生活中的队列(先排队的先办完事)。

队列有下面几个操作:
- InitQueue() ——初始化队列
- EnQueue() ——进队列
- DeQueue() ——出队列
- IsQueueEmpty()——判断队列是否为空
- IsQueueFull() ——判断队列是否已满
队列可以由数组和链表两种形式实现队列操作(c语言),下面仅以数组为例:
数组实现:
队列数据结构
typedef struct queue { int queuesize; //数组的大小 int head, tail; //队列的头和尾下标 int *q; //数组头指针 }Queue;
InitQueue() ——初始化队列
void InitQueue(Queue *Q) { Q->queuesize = 8; Q->q = (int *)malloc(sizeof(int) * Q->queuesize); //分配内存 Q->tail = 0; Q->head = 0; }

这样有个缺陷,空间利用率不高。采用循环队列:

EnQueue() ——进队列
void EnQueue(Queue *Q, int key) { int tail = (Q->tail+1) % Q->queuesize; //取余保证,当quil=queuesize-1时,再转回0 if (tail == Q->head) //此时队列没有空间 { printf("the queue has been filled full!"); } else { Q->q[Q->tail] = key; Q->tail = tail; } }

DeQueue() ——出队列
int DeQueue(Queue *Q) { int tmp; if(Q->tail == Q->head) //判断队列不为空 { printf("the queue is NULL\n"); } else { tmp = Q->q[q->head]; Q->head = (Q->head+1) % Q->queuesize; } return tmp; }
IsQueueEmpty()——判断队列是否为空
int IsQueueEmpty(Queue *Q) { if(Q->head == Q->tail) { return 1; } else { return 0; } }
IsQueueFull()——判断队列是否已满
int IsQueueFull(Queue *Q) { if((Q->tail+1)% Q->queuesize == Q->head) { return 1; } else { return 0; } }
优先队列:
队列(queue)维护了一组对象,进入队列的对象被放置在尾部,下一个被取出的元素则取自队列的首部。priority_queue特别之处在于,允许用户为队列中存储的元素设置优先级。这种队列不是直接将新元素放置在队列尾部,而是放在比它优先级低的元素前面。标准库默认使用<操作符来确定对象之间的优先级关系,所以如果要使用自定义对象,需要重载 < 操作符。
优先队列有两种,一种是最大优先队列;一种是最小优先队列;每次取自队列的第一个元素分别是优先级最大和优先级最小的元素。
1) 优先队列的定义
包含头文件:"queue.h", "functional.h"
可以使用具有默认优先级的已有数据结构;也可以再定义优先队列的时候传入自定义的优先级比较对象;或者使用自定义对象(数据结构),但是必须重载好< 操作符。
2) 优先队列的常用操作
| 优先级队列支持的操作 |
| q.empty() 如果队列为空,则返回true,否则返回false q.size() 返回队列中元素的个数 q.pop() 删除队首元素,但不返回其值 q.top() 返回具有最高优先级的元素值,但不删除该元素 q.push(item) 在基于优先级的适当位置插入新元素 |
其中q.top()为查找操作,在最小优先队列中搜索优先权最小的元素,在最大优先队列中搜索优先权最大的元素。q.pop()为删除该元素。优先队列插入和删除元素的复杂度都是O(lgn),所以很快
在优先队列中,优先级高的元素先出队列。标准库默认使用元素类型的<操作符来确定它们之间的优先级关系。
优先队列的第一种用法,也是最常用的用法:
- priority_queue<int> qi;
通过<操作符可知在整数中元素大的优先级高。
故示例1中输出结果为:9 6 5 3 2
第二种方法:
在示例1中,如果我们要把元素从小到大输出怎么办呢?
这时我们可以传入一个比较函数,使用functional.h函数对象作为比较函数。
- priority_queue<int, vector<int>, greater<int> > qi2;
其中
第二个参数为容器类型。
第三个参数为比较函数。
故示例2中输出结果为:2 3 5 6 9
第三种方法:自定义优先级。
- struct node
- {
- friend bool operator< (node n1, node n2)
- {
- return n1.priority < n2.priority;
- }
- int priority;
- int value;
- };
在该结构中,value为值,priority为优先级。
通过自定义operator<操作符来比较元素中的优先级。
在示例3中输出结果为:
优先级 值
9 5
8 2
6 1
2 3
1 4
但如果结构定义如下:
- struct node
- {
- friend bool operator> (node n1, node n2)
- {
- return n1.priority > n2.priority;
- }
- int priority;
- int value;
- };
则会编译不过(G++编译器)因为标准库默认使用元素类型的<操作符来确定它们之间的优先级关系。而且自定义类型的<操作符与>操作符并无直接联系,故会编译不过。
//代码清单
- #include<iostream>
- #include<functional>
- #include<queue>
- using namespace std;
- struct node
- {
- friend bool operator< (node n1, node n2)
- {
- return n1.priority < n2.priority;
- }
- int priority;
- int value;
- };
- int main()
- {
- const int len = 5;
- int i;
- int a[len] = {3,5,9,6,2};
- //示例1
- priority_queue<int> qi;
- for(i = 0; i < len; i++)
- qi.push(a[i]);
- for(i = 0; i < len; i++)
- {
- cout<<qi.top()<<" ";
- qi.pop();
- }
- cout<<endl;
- //示例2
- priority_queue<int, vector<int>, greater<int> >qi2;
- for(i = 0; i < len; i++)
- qi2.push(a[i]);
- for(i = 0; i < len; i++)
- {
- cout<<qi2.top()<<" ";
- qi2.pop();
- }
- cout<<endl;
- //示例3
- priority_queue<node> qn;
- node b[len];
- b[0].priority = 6; b[0].value = 1;
- b[1].priority = 9; b[1].value = 5;
- b[2].priority = 2; b[2].value = 3;
- b[3].priority = 8; b[3].value = 2;
- b[4].priority = 1; b[4].value = 4;
- for(i = 0; i < len; i++)
- qn.push(b[i]);
- cout<<"优先级"<<'\t'<<"值"<<endl;
- for(i = 0; i < len; i++)
- {
- cout<<qn.top().priority<<'\t'<<qn.top().value<<endl;
- qn.pop();
- }
- return 0;
- }

另外贴一段优先队列使用的代码:
- #include<iostream>
- #include<functional>
- #include<queue>
- #include<vector>
- using namespace std;
- struct cmp1
- {
- bool operator () (int &a, int &b)
- {
- return a > b ; // 从小到大排序,值 小的 优先级别高
- }
- };
- struct cmp2
- {
- bool operator () (int &a, int &b)
- {
- return a < b; // 从大到小
- }
- };
- struct number1
- {
- int x;
- bool operator < (const number1 &a)const
- {
- return x > a.x; // 从小到大 ,x 小的 优先级别高
- }
- };
- struct number2
- {
- int x;
- bool operator < (const number2 &a)const
- {
- return x < a.x; // 从大到小 ,x 大的优先级别高
- }
- };
- int a[] = {14,10,56,7,83,22,36,91,3,47,72,0};
- number1 num1[] ={14,10,56,7,83,22,36,91,3,47,72,0};
- number2 num2[] ={14,10,56,7,83,22,36,91,3,47,72,0};
- int main()
- {
- priority_queue<int>que; // 采用默认优先级构造队列 从大到小。
- priority_queue<int, vector<int>, cmp1 >que1;
- priority_queue<int, vector<int>, cmp2 >que2;
- priority_queue<int, vector<int>, greater<int> > que3; //functional 头文件自带的
- priority_queue<int, vector<int>, less<int> > que4; //functional 头文件自带的
- priority_queue<number1> que5;
- priority_queue<number2> que6;
- int i;
- for(i=0;a[i];i++)
- {
- que.push(a[i]);
- que1.push(a[i]);
- que2.push(a[i]);
- que3.push(a[i]);
- que4.push(a[i]);
- }
- for(i=0;num1[i].x;i++)
- que5.push(num1[i]);
- for(i=0;num2[i].x;i++)
- que6.push(num2[i]);
- printf("采用默认优先关系:\n(priority_queue<int>que;)\n");
- printf("Queue 0:\n");
- while(!que.empty())
- {
- printf("%3d",que.top());
- que.pop();
- }
- puts("");
- puts("");
- printf("采用结构体自定义优先级方式一:\n(priority_queue<int,vector<int>,cmp>que;)\n");
- printf("Queue 1:\n");
- while(!que1.empty())
- {
- printf("%3d",que1.top());
- que1.pop();
- }
- puts("");
- printf("Queue 2:\n");
- while(!que2.empty())
- {
- printf("%3d",que2.top());
- que2.pop();
- }
- puts("");
- puts("");
- printf("采用头文件\"functional\"内定义优先级:\n(priority_queue<int, vector<int>,greater<int>/less<int> >que;)\n");
- printf("Queue 3:\n");
- while(!que3.empty())
- {
- printf("%3d",que3.top());
- que3.pop();
- }
- puts("");
- printf("Queue 4 :\n");
- while(!que4.empty())
- {
- printf("%3d",que4.top());
- que4.pop();
- }
- puts("");
- puts("");
- printf("采用结构体自定义优先级方式二:\n(priority_queue<number>que)\n");
- printf("Queue 5:\n");
- while(!que5.empty())
- {
- printf("%3d",que5.top());
- que5.pop();
- }
- puts("");
- printf("Queue 6:\n");
- while(!que6.empty())
- {
- printf("%3d",que6.top());
- que6.pop();
- }
- return 0;
- }
执行结果:

三、栈(Stack)
栈(statck)这种数据结构在计算机中是相当出名的。栈中的数据是先进后出的(First In Last Out, FILO)。栈只有一个出口,允许新增元素(只能在栈顶上增加)、移出元素(只能移出栈顶元素)、取得栈顶元素等操作。在STL中,栈是以别的容器作为底部结构,再将接口改变,使之符合栈的特性就可以了。因此实现非常的方便。下面就给出栈的函数列表和VS2008中栈的源代码,在STL中栈一共就5个常用操作函数(top()、push()、pop()、 size()、empty() ),很好记的。
堆栈是一个线性表,插入和删除只在表的一端进行。这一端称为栈顶(Stack Top),另一端则为栈底(Stack Bottom)。堆栈的元素插入称为入栈,元素的删除称为出栈。由于元素的入栈和出栈总在栈顶进行,因此,堆栈是一个后进先出(Last In First Out)表,即 LIFO 表。
C++ STL 的堆栈泛化是直接通过现有的序列容器来实现的,默认使用双端队列deque的数据结构,当然,可以采用其他线性结构(vector 或 list等),只要提供堆栈的入栈、出栈、栈顶元素访问和判断是否为空的操作即可。由于堆栈的底层使用的是其他容器,因此,堆栈可看做是一种适配器,将一种容器转换为另一种容器(堆栈容器)。
为了严格遵循堆栈的数据后进先出原则,stack 不提供元素的任何迭代器操作,因此,stack 容器也就不会向外部提供可用的前向或反向迭代器类型。
stack堆栈容器的C++标准头文件为 stack ,必须用宏语句 "#include <stack>" 包含进来,才可对 stack 堆栈的程序进行编译。

VS2008栈的源代码
友情提示:初次阅读时请注意其实现思想,不要在细节上浪费过多的时间。
- //VS2008中 stack的定义 MoreWindows整理(http://blog.csdn.net/MoreWindows)
- template<class _Ty, class _Container = deque<_Ty> >
- class stack
- { // LIFO queue implemented with a container
- public:
- typedef _Container container_type;
- typedef typename _Container::value_type value_type;
- typedef typename _Container::size_type size_type;
- typedef typename _Container::reference reference;
- typedef typename _Container::const_reference const_reference;
- stack() : c()
- { // construct with empty container
- }
- explicit stack(const _Container& _Cont) : c(_Cont)
- { // construct by copying specified container
- }
- bool empty() const
- { // test if stack is empty
- return (c.empty());
- }
- size_type size() const
- { // test length of stack
- return (c.size());
- }
- reference top()
- { // return last element of mutable stack
- return (c.back());
- }
- const_reference top() const
- { // return last element of nonmutable stack
- return (c.back());
- }
- void push(const value_type& _Val)
- { // insert element at end
- c.push_back(_Val);
- }
- void pop()
- { // erase last element
- c.pop_back();
- }
- const _Container& _Get_container() const
- { // get reference to container
- return (c);
- }
- protected:
- _Container c; // the underlying container
- };
可以看出,由于栈只是进一步封装别的数据结构,并提供自己的接口,所以代码非常简洁,如果不指定容器,默认是用deque来作为其底层数据结构的(对deque不是很了解?可以参阅《STL系列之一 deque双向队列》)。下面给出栈的使用范例:
- //栈 stack支持 empty() size() top() push() pop()
- // by MoreWindows(http://blog.csdn.net/MoreWindows)
- #include <stack>
- #include <vector>
- #include <list>
- #include <cstdio>
- using namespace std;
- int main()
- {
- //可以使用list或vector作为栈的容器,默认是使用deque的。
- stack<int, list<int>> a;
- stack<int, vector<int>> b;
- int i;
- //压入数据
- for (i = 0; i < 10; i++)
- {
- a.push(i);
- b.push(i);
- }
- //栈的大小
- printf("%d %d\n", a.size(), b.size());
- //取栈项数据并将数据弹出栈
- while (!a.empty())
- {
- printf("%d ", a.top());
- a.pop();
- }
- putchar('\n');
- while (!b.empty())
- {
- printf("%d ", b.top());
- b.pop();
- }
- putchar('\n');
- return 0;
- }
四、完全二叉树与满二叉树
满二叉树(Full Binary Tree):
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点(最后一层上的无子结点的结点为叶子结点)。也可以这样理解,除叶子结点外的所有结点均有两个子结点。节点数达到最大值。所有叶子结点必须在同一层上.
一颗树深度为h,最大层数为k,深度与最大层数相同,k=h;
完全二叉树(Complete Binary Tree)
完全二叉树的节点个数是任意的,从形式上来说他是一个可能有缺失的三角形,但所缺部分肯定是右下角的某个连续部分。这样说不玩整,更准确来说,我们可以说他和满二叉树的区别是,他的最后一行可能不是完整的,但绝对是右方的连续部分缺失。可能听起来有点乱,用数学公式讲,对于K层的完全二叉树,其节点数的范围是2^(k-1)-1<N<2^k-1。
1 1
/ \ / \
1 1 1 1
/ \ / \ / \
1 1 1 1 1 1 满二叉树 完全二叉树
一棵深度为k且有2的k次方减1个结点的二叉树是满二叉树。 深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称为完全二叉树。
霍夫曼树:每个节点要么没有子节点,要么有两个子节点。
五、哈希表
一、哈希表法简介
哈希表(Hash table,也叫散列表),是根据关键字(Key Value)而直接访问在内存存储位置的数据结构。也就是说,它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度。这个映射函数称做散列函数,存放记录的数组称做散列表。
若关键字为k,则其值存放在f(k)的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系f为散列函数,按这个思想建立的表为哈希表。
二、哈希冲突
对不同的关键字可能得到同一散列地址,即k1≠k2,而f(k1)=f(k2),这种现象称为冲突。具有相同函数值的关键字对该散列函数来说称做同义词。
三、构造哈希函数的方法
(1)直接定址法
思想:取关键字或关键字的某个线性函数值为散列地址。即hash(k)=k或hash(k)=ak + b,其中a,b为常数 。
特点:对于不同的关键字不会产生冲突,缺点是由于关键字集合很少是连续的,会造成空间的大量浪费。
(2)除留余数法
思想:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即hash(k)=k mod p, p≤m。不仅可以对关键字直接取模,也可在折叠法、平方取中法等运算之后取模。
特点:对p的选择很重要,一般取小于m的最大素数,若p选择不好,容易产生冲突。
(3)数字分析法
思想:假设关键字是以r为基的数,并且哈希表中可能出现的关键字都是事先知道的,则可选取关键字的若干数位组成哈希地址。
特点:需要对关键字进行分析。
(4)平方取中法
思想:取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况,取其中的哪几位也不一定合适,而一个数平方后的中间几位数和数的每一位都相关,由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
(5)折叠法
思想:将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址。
四、解决哈希冲突的方法
(1)开放地址法
开放地址的基本思想是在发生冲突时,按照某种方法继续探测基本表中的其他存储单元,直到找到空位置为止。
增量di可以有不同的取法:
1、di = 1, 2, 3, ... , m-1; 线性探测再散列
2、di = 1^2, -1^2, 2^2, -2^2, 3^2,…,±(k)^2,(k<=m/2);二次探测再散列;
3、di = 伪随机数 ; 伪随机再散列
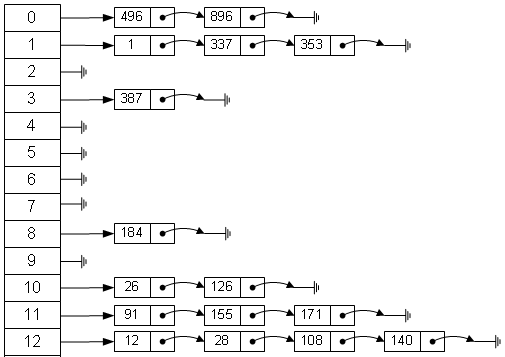
(2)链地址法
将所有具有相同哈希地址的记录放在同一单链表中,哈希表的第i个元素存放哈希地址为i的记录组成的单链表的头指针。
(3)建立一个公共溢出区
一旦产生冲突,均把当前记录放入公共溢出区的当前表尾。
2、哈希表详解
3、理解哈希表




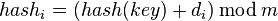

 京公网安备 11010502036488号
京公网安备 11010502036488号