LeetCode 1091. Shortest Path in Binary Matrix二进制矩阵中的最短路径【Medium】【Python】【BFS】

Problem

LeetCode

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

  • Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
  • C_1 is at location (0, 0) (ie. has value grid[0][0])
  • C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
  • If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom-right. If such a path does not exist, return -1.

Example 1:

Input: [[0,1],[1,0]]
Output: 2

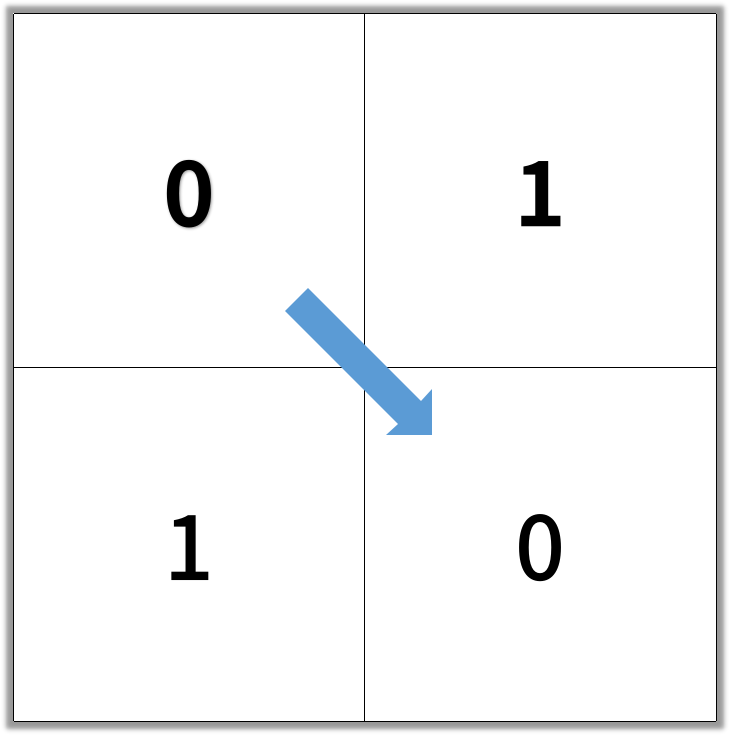
Example 2:

Input: [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

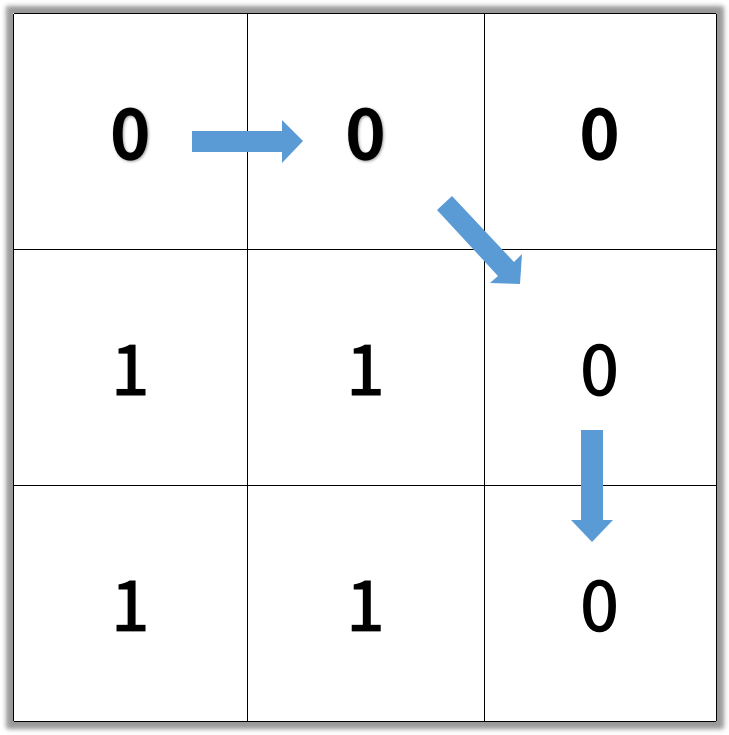
Note:

  1. 1 <= grid.length == grid[0].length <= 100
  2. grid[r][c] is 0 or 1

问题

力扣

在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。

一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, ..., C_k 组成：

相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通（此时，C_i 和 C_{i+1} 不同且共享边或角）

  • C_1 位于 (0, 0)（即，值为 grid[0][0]）

  • C_k 位于 (N-1, N-1)（即，值为 grid[N-1][N-1]）

  • 如果 C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）

    返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径，返回 -1 。

示例 1：

输入：[[0,1],[1,0]]
输出：2

示例 2：

输入：[[0,0,0],[1,1,0],[1,1,0]]
输出：4

提示：

  1. 1 <= grid.length == grid[0].length <= 100
  2. grid[i][j]为 0 或 1

思路

BFS

最短路径问题，可以使用 BFS 来解。
在队列中直接添加路径长度 cnt 即可。

BFS模板

void BFS(){
    判断边界条件，是否能直接返回结果的。

    定义队列；
    定义备忘录，用于记录已经访问的位置；

    将起始位置加入到队列中，同时更新备忘录。

    while (队列不为空){
        获取当前队列中的元素个数。
        判断是否到达终点位置。

        for (元素个数){
            取出一个位置节点。
            判断是否到达终点位置。
            获取它对应的下一个所有的节点。
            条件判断，过滤掉不符合条件的位置。
            新位置重新加入队列。
        }
    }
}

BFS模板地址

时间复杂度: O(N^2)
空间复杂度: O(N^2)

Python3代码

class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        if grid[0][0] == 1 or grid[-1][-1] == 1:  # top-left is not empty or bottom-right is not empty
            return -1

        # eight directions: → ← ↓ ↑ ↗ ↙ ↖ ↘
        directions = [[1, 0], [-1, 0], [0, -1], [0, 1], [1, 1], [1, -1], [-1, 1], [-1, -1]]

        queue = [(0, 0, 1)]  # location, cnt
        n = len(grid)

        # BFS
        while len(queue):
            x0, y0, cnt = queue.pop(0)  # pop (location, cnt)
            if x0 == n - 1 and y0 == n - 1:  # already arrive at bottom-right
                return cnt

            # eight directions
            for i, j in directions:
                x, y = x0 + i, y0 + j
                # (x, y) is in the grid and grid[x][y] = 0, also means: grid[x][y] is not visited
                if 0 <= x < n and 0 <= y < n and not grid[x][y]:
                    queue.append((x, y, cnt + 1))
                    grid[x][y] = 1  # visited

        return -1

代码地址

GitHub链接