基础数据结构——1.2队列

洛谷 P1540 [NOIP2010 提高组]机器翻译

时间限制：1.00s　　内存限制：125.00MB

题目背景

小晨的电脑上安装了一个机器翻译软件，他经常用这个软件来翻译英语文章。

题目描述

这个翻译软件的原理很简单，它只是从头到尾，依次将每个英文单词用对应的中文含义来替换。对于每个英文单词，软件会先在内存中查找这个单词的中文含义，如果内存中有，软件就会用它进行翻译；如果内存中没有，软件就会在外存中的词典内查找，查出单词的中文含义然后翻译，并将这个单词和译义放入内存，以备后续的查找和翻译。

假设内存中有 $MM$ 个单元，每单元能存放一个单词和译义。每当软件将一个新单词存入内存前，如果当前内存中已存入的单词数不超过 $M-1M-1$，软件会将新单词存入一个未使用的内存单元；若内存中已存入 $MM$ 个单词，软件会清空最早进入内存的那个单词，腾出单元来，存放新单词。

假设一篇英语文章的长度为 $NN$ 个单词。给定这篇待译文章，翻译软件需要去外存查找多少次词典？假设在翻译开始前，内存中没有任何单词。

输入格式

共 $22$ 行。每行中两个数之间用一个空格隔开。

第一行为两个正整数 $M,NM,N$，代表内存容量和文章的长度。

第二行为 $NN$ 个非负整数，按照文章的顺序，每个数（大小不超过 $10001000$）代表一个英文单词。文章中两个单词是同一个单词，当且仅当它们对应的非负整数相同。

输出格式

一个整数，为软件需要查词典的次数。

样例输入

3 7
1 2 1 5 4 4 1

样例输出

5

样例解释

整个查字典过程如下：每行表示一个单词的翻译，冒号前为本次翻译后的内存状况：

1. 1：查找单词 1 并调入内存。
2. 1 2：查找单词 2 并调入内存。
3. 1 2：在内存中找到单词 1。
4. 1 2 5：查找单词 5 并调入内存。
5. 2 5 4：查找单词 4 并调入内存替代单词 1。
6. 2 5 4：在内存中找到单词 4。
7. 5 4 1：查找单词 1 并调入内存替代单词 2。

共计查了 $55$ 次词典。

数据范围

• 对于 $10\mathrm{\%}10\backslash \%$ 的数据有 $M=1M=1$，$N\le 5N\; \backslash leq\; 5$；
• 对于 $100\mathrm{\%}100\backslash \%$ 的数据有 $1\le M\le 1001\; \backslash leq\; M\; \backslash leq\; 100$，$1\le N\le 10001\; \backslash leq\; N\; \backslash leq\; 1000$。

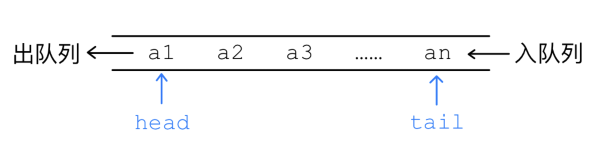
队列顾名思义，有队首 $headhead$ 和队尾 $tailtail$，队列内的元素是讲究顺序的，新的元素只能从队尾放入，队列内的元素只能按照入队顺序从队首取出.

队列如图1.2.1所示，其中 $a1\sim ana1\backslash sim\; an$ 代表队列内的元素.

图1.2.1 队列

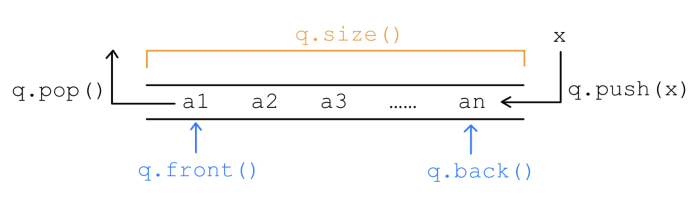
STL queue 的部分基本操作¹

C++ STL中有封装好的队列（queue）容器，引用 queue 头文件即可使用，其有如下几种基本操作：

• queue<T> q：定义存储元素的数据类型为 T 的队列变量，其变量名为 q.

• q.front()：返回队列 q 队首的元素.

• q.back()：返回队列 q 队尾的元素.

• q.push(x)：将 x 放入队列 q 的队尾.

• q.pop()：将队列 q 的队首元素删除.

• q.size()：返回队列 q 内的元素个数.

• q.empty()：检查队列 q 是否为空，若队列 q 中没有元素则返回 true，否则返回 false.

使用 q.front()、q.pop() 这类直接调用队列内元素的函数时，要注意先判断队列是否为空.

如果队列为空就使用这些函数会导致程序运行时错误（Runtime Error）.

STL queue 的部分基本操作如图1.2.2所示.

图1.2.2 STL queue 的部分基本操作

STL queue 和链表一样，不能随机访问队列内的元素.

即试图用 q[2] 来获得队列 q 中的第三个元素是不可行的.

代码实现

由于英文文章的总单词数量为 $N⩽1000N\backslash leqslant\; 1000$，可以考虑使用数组 $in\mathrm{\_}quein\backslash \_que$ 来表示单词是否在翻译软件的内存中，即：

• 若 $in\mathrm{\_}que[i]=1in\backslash \_que[i]=1$，则说明单词 $ii$ 在翻译软件的内存中.
• 若 $in\mathrm{\_}que[i]=0in\backslash \_que[i]=0$，则说明单词 $ii$ 不在翻译软件的内存中.

翻译软件的内存就相当于队列，则：

1. 若所有单词都翻译完了，则算法结束，否则跳转到 2.
2. 读入新的单词 $xx$，若 $in\mathrm{\_}que[x]=1in\backslash \_que[x]=1$，则直接用翻译软件翻译即可，跳转到 1；否则跳转 3.
3. 读入的单词不在翻译软件的内存中，则需要去外存查找该单词并将其入队，若队列已满则需要让队首单词出队，跳转到 1.

如下为使用 STL queue 的参考代码.

//洛谷P1540机器翻译-STL queue 写法
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int in_que[N]; // in_que[i] 表示单词 i 是否在队列中
int main() {
	int m, n; scanf("%d%d", &m, &n);
	queue<int>q;
	int ans = 0;
	while (n--) {
		int x; scanf("%d", &x);
		if (in_que[x]) continue;
		if (q.size() == m) { in_que[q.front()] = 0; q.pop(); }
		/*
			这里要先执行 in_que[q.front()]=0
			如果先执行 q.pop()，删除的队首元素就找不到了
		*/
		in_que[x] = 1; q.push(x); ++ans;
	}
	printf("%d", ans);
	return 0;
}

时间复杂度分析

最多只有 $nn$ 个不同的单词，队列本身的操作都不消耗时间，故时间复杂度为 $O(n)O(n)$.

1.2.2 手写循环队列

创建队列

队列内元素个数 size()

可以使用结构体数组或多个数组（若队列内单个元素存储多种信息）来实现队列，但一般有如下的情况出现：

• 最多只有 $n-1n-1$ 个元素保存在队列内.
• 某些元素可能会反复出队入队.

在这样的情况下，单纯定义长度为 $nn$ 的数组是解决不了这一问题的.

可以将队首元素被删除后空下来数组内的空间利用起来，这样就可以解决这一问题了.

定义队列保存在数组 $queque$ 内，$headhead$ 为数组内队首元素的下标，$tailtail$ 为数组内队尾元素的下标.

也就是说，这里定义的队列在数组内 $[head,tail][head,tail]$ 这一闭区间范围的.

在有些场合中，$tailtail$ 为数组内队尾元素的后一个位置的下标，即定义队列在 $[head,tail)[head,tail)$ 这一左闭右开区间范围的.

首先定义队列内元素的个数 $que\mathrm{\_}sizeque\backslash \_size$，有：

这个算式需要分两种情况进行讨论：

1. $head⩽tailhead\; \backslash leqslant\; tail$，此时 $tail-head+1tail-head+1$ 即为队列的长度.
2. ，此时队列并不一定为空，可能是因为利用了之前的空间导致 $tailtail$ 的所指向的元素下标小于 $headhead$ 所指向的元素的下标而已，也就是说此时数组内的队列在 $[head,n)\cup [0,tail][head,n)\; \backslash cup\; [0,tail]$ 这个范围内，此时所求的 $tail-head+1tail-head+1$ 是一个负数，其绝对值表示数组中不在队列内的下标的个数，那么 $tail-head+1+ntail-head+1+n$ 就是队列内元素的个数.

两种情况如下图1.2.3所示.

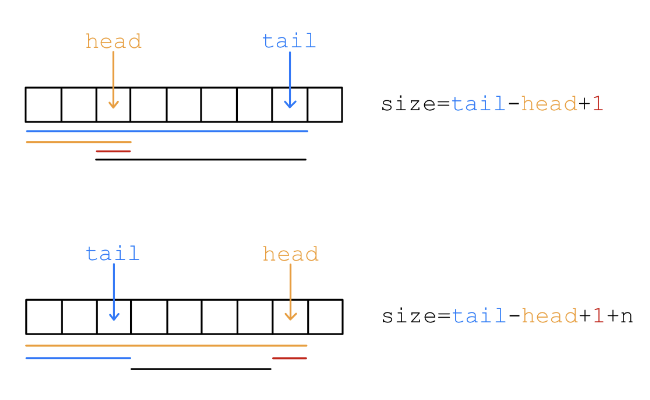
图1.2.3 循环队列的 size

初始化队列 init_que()

在一开始，队列为空，则设 $head=0head=0$，$tail=-1tail=-1$.

当队列为空时应该有 $que\mathrm{\_}size=0que\backslash \_size=0$，但这里有一个问题，若队列放满了 $nn$ 个元素，此时 $tail=(head-1+n)\mathrm{\%}ntail=(head-1+n)\backslash \%n$ 也会导致 $que\mathrm{\_}size=0que\backslash \_size=0$.

所以上面才会说开辟队列数组大小 $nn$，但队列最多存放 $n-1n-1$ 个元素，这样就可以规避这个问题了.

有如下代码片段：

//代码片段-init_que() 和 size() 和 empty()
//初始化队列
void init_que() {
	head = 0;
	tail = -1;
}
//返回队列内元素个数
int size() {
	return (tail - head + 1 + n) % n;
}
//判断队列是否为空
bool empty() {
	return size() ? 1 : 0;
}

放入元素和删除元素

在队尾放入元素 push(x)

设要放入的元素为 $xx$，则：

1. $tail=(tail+1)\mathrm{\%}ntail=(tail+1)\backslash \%n$，先让队尾往后走一格，腾出空间放置 $xx$，这里注意如果 $tailtail$ 超过了数组 $queque$ 的末尾（$que[n-1]que[n-1]$）就会回到数组 $queque$ 的开头（$que[0]que[0]$）.
2. $que[tail]=xque[tail]=x$，放置 $xx$.

有如下代码片段：

//代码片段-push(x)
void push(int x) {
	tail = (tail + 1) % n;
	que[tail] = x;
}

删除队首元素 pop(x)

删除队首元素直接让 $head=(head+1)\mathrm{\%}nhead=(head+1)\backslash \%n$ 即可，在这之前无需对 $que[head]que[head]$ 进行任何操作（因为之后如果放入元素会将这个位置的数据覆盖掉）.

有如下代码片段：

//代码片段-pop()
void pop() {
	head = (head + 1) % n;
}

输出当前队列内的第 $kk$ 个元素 kth()

由于此循环队列是基于数组实现了，想要查找队列内的第 $kk$ 个（从 $11$ 开始计数）元素是十分容易的.

有如下代码片段：

//代码片段-kth()
int kth(int k) {
	return que[(head + k -1) % n];
}

这里实现的函数也没有检查队列是否为空（是否有至少 $kk$ 个元素），所以在使用时需要多加小心.

代码实现

与 STL queue 的版本没有什么区别，只是队列需要自己用数组实现.

如下为使用数组实现循环链表的参考代码.

//洛谷P1540机器翻译-循环队列写法
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int in_que[N];
int que[N],head,tail;
void init_que() {
	head = 0;
	tail = -1;
}
int size() {
	return (tail - head + 1 + N) % N;
}
void push(int x) {
	tail = (tail + 1) % N;
	que[tail] = x;
}
void pop() {
	head = (head + 1) % N;
}
int main() {
	int m, n; scanf("%d%d", &m, &n);
	int ans = 0;
	while (n--) {
		int x; scanf("%d", &x);
		if (in_que[x]) continue;
		if (size() == m) { in_que[que[head]] = 0; pop(); }
		in_que[x] = 1; push(x); ++ans;
	}
	printf("%d", ans);
	return 0;
}

时间复杂度分析

数组模拟的效率和 STL queue 没有太多区别，时间复杂度仍为 $O(n)O(n)$.

1.2.3 双端队列和单调队列

双端队列 deque

C++ STL中有封装好的**双端队列（deque）**容器，引用头文件 deque 即可使用，其相较队列有以下几个优点：

• 可以随机访问双端队列中的第 $kk$ 个元素.
• 可以在队首/队尾进行添加/删除元素的操作.

其有如下几种基本操作：

• deque<T> q：定义存储元素的数据类型为 T 的双端队列变量，其变量名为 q.

• q.front()：返回队列 q 队首的元素.

• q.back()：返回队列 q 队尾的元素.

• q[k] 或 q.at(k)：返回队列 q 下标为 $kk$ 的元素（从 $00$ 开始计数）.

• q.push_front(x)：将 x 放入队列 q 的队首.

• q.push_back(x)：将 x 放入队列 q 的队尾.

• q.pop_front()：将队列 q 的队首元素删除.

• q.pop_back()：将队列 q 的队尾元素删除

• q.size()：返回队列 q 内的元素个数.

• q.empty()：检查队列 q 是否为空，若队列 q 中没有元素则返回 true，否则返回 false.

使用 q.front()、q.back()、q[k]、q.at(k)、q.pop_front()、q.pop_back() 这类调用双端队列内元素的函数（或功能）时，

要注意先判断双端队列内是否有这样的元素.

洛谷 P1886 滑动窗口/【模板】单调队列

时间限制：1.00s　　内存限制：125.00MB

题目描述

有一个长为 $nn$ 的序列 $aa$，以及一个大小为 $kk$ 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is $[1,3,-1,-3,5,3,6,7][1,3,-1,-3,5,3,6,7]$, and $k=3k\; =\; 3$。

Window position	Minimum value	Maximum value
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7

输入格式

输入一共有两行，第一行有两个正整数 $n,kn,k$。 第二行 $nn$ 个整数，表示序列 $aa$

输出格式

输出共两行，第一行为每次窗口滑动的最小值 第二行为每次窗口滑动的最大值

样例输入

8 3
1 3 -1 -3 5 3 6 7

样例输出

-1 -3 -3 -3 3 3
3 3 5 5 6 7

数据范围

对于 $50\mathrm{\%}50\backslash \%$ 的数据，$1\le n\le 10^{5}1\; \backslash le\; n\; \backslash le\; 10^5$； 对于 $100\mathrm{\%}100\backslash \%$ 的数据，$1\le k\le n\le 10^{6}1\backslash le\; k\; \backslash le\; n\; \backslash le\; 10^6$，$a_i\in [-2^{31},2^{31})a\_i\; \backslash in\; [-2^\{31\},2^\{31\})$。

单调队列

单调队列是指队列内的元素按照入队顺序、以某种规则呈现出（非）递增/递减的特点的队列.

考虑求滑动窗口中的最小值，可以构建一个单调队列（一般用 deque 实现）.

从头到尾遍历序列 $aa$，设当前遍历到了序列 $aa$ 的第 $ii$ 个数（视为滑动窗口的右端点为 $ii$），则：

1. 检查队首元素是否在滑动窗口内，如果其超出了滑动窗口的范围则删除队首元素，直到队列为空或队首元素在滑动窗口内，跳转到 2.
2. 检查队尾元素是否大于 $a_{i}a\_i$，若大于则删除队尾元素，直到队列为空或队尾元素小于 $a_{i}a\_i$，将 $a_{i}a\_i$ 放入队尾，跳转到 3.
3. 若滑动窗口范围内的元素数量少于 $mm$，则直接跳转到 4，否则队首元素即为序列 $aa$ 的 $[i-m+1,i][i-m+1,i]$ 范围内的最小值，将其记录后再跳转到 4.
4. 若序列 $aa$ 遍历完则结束算法，否则遍历到序列 $aa$ 的下一个数（移动滑动窗口），即 $i=i+1i=i+1$，跳转到 1.

这样可以保证：

• 队列内的元素是递增的，因为 2 保证了将 $a_{i}a\_i$ 放入队尾时，队列内的元素都是小于 $a_{i}a\_i$ 的.
• 当序列 $aa$ 遍历到第 $ii$ 个数时，$a_{i}a\_i$ 已经放入队尾，若此时队列内的某一部分的元素为 $a_x,a_y,a_{z}a\_x,a\_y,a\_z$，则其保证了 $a_{y}a\_y$ 是序列 $aa$ 的 $[x+1,i][x+1,i]$ 范围内的最小值.
  • 因为队列内的元素是递增的，有 .
  • 若 $a_{y}a\_y$ 前面没有 $a_{x}a\_x$ 存在，则 $a_{y}a\_y$ 是序列 $aa$ 的 $[i-m+1,i][i-m+1,i]$ 范围内的最小值.
  • 即使 $a_{y}a\_y$ 后面没有 $a_{z}a\_z$，其也满足是序列 $aa$ 的 $[x+1,i][x+1,i]$ 范围内的最小值.

求最大值同理，只要构建一个递减的单调队列即可.

代码实现

在代码实现时，为了方便知道队首元素是否在滑动窗口内，这里并不在单调队列中直接存序列 $aa$ 的具体元素的值，而是存储其下标.

如下为使用 STL deque 的参考代码.

//洛谷P1886滑动窗口-deque写法
#include<bits/stdc++.h>
using namespace std;
const int N = 1000005;
int a[N];
int ans_min[N], ans_max[N];
int main() {
	int n, m; scanf("%d %d", &n, &m);
	deque<int>q_min, q_max;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		while (!q_min.empty() && i - m + 1 > q_min.front()) q_min.pop_front();
		while (!q_max.empty() && i - m + 1 > q_max.front()) q_max.pop_front();
		while (!q_min.empty() && a[q_min.back()] >= a[i]) q_min.pop_back();
		while (!q_max.empty() && a[q_max.back()] <= a[i]) q_max.pop_back();
		q_min.push_back(i);
		q_max.push_back(i);
		if (i >= m) {
			ans_min[i] = a[q_min.front()];
			ans_max[i] = a[q_max.front()];
		}
	}
	for (int i = m; i <= n; ++i) printf("%d ", ans_min[i]);
	printf("\n");
	for (int i = m; i <= n; ++i) printf("%d ", ans_max[i]);
	return 0;
}

时间复杂度分析

这份代码看似有多个 while 循环，但是队列内的元素不超过 $nn$ 个，而且被删除的元素之后也不会再放入队列，故每个 while 最多被执行 $nn$ 次.

再考虑序列 $aa$ 只有 $nn$ 个数字，总的时间复杂度为 $O(n+n)=O(n)O(n+n)=O(n)$.

习题

洛谷 P2776 [SDOI2007]小组队列

时间限制：1.00s　　内存限制：125.00MB

题目描述

有 $mm$ 个小组，$nn$ 个元素，每个元素属于且仅属于一个小组。

支持以下操作：

push x：使元素 x 进队，如果前边有 x 所属小组的元素，x 会排到自己小组最后一个元素的下一个位置，否则 x 排到整个队列最后的位置。

pop：出队，弹出队头并输出出队元素，出队的方式和普通队列相同，即排在前边的元素先出队。

输入格式

第一行有两个正整数 $nn$, $mm$，分别表示元素个数和小组个数，元素和小组均从 $00$ 开始编号。

接下来一行 $nn$ 个非负整数 $A_{i}A\_i$，表示元素 $ii$ 所在的小组。

接下来一行一个正整数 $TT$ ，表示操作数。

接下来 $TT$ 行，每行为一个操作。

输出格式

对于每个出队操作输出一行，为出队的元素。

样例输入

4 2
0 0 1 1
6
push 2
push 0
push 3
pop
pop
pop

样例输出

2
3
0

提示

对于 $30\mathrm{\%}30\backslash \%$ 的数据，$1\le n\le 1001\le n\le 100$，$1\le m\le 101\le m\le 10$，$T\le 50T\le 50$。

对于 $100\mathrm{\%}100\backslash \%$ 的数据，$1\le n\le 1000001\le n\le 100000$，$1\le m\le 3001\le m\le 300$，$T\le 100000T\le 100000$，输入保证操作合法。

题解

使用两个队列，队列 $lislis$ 表示小组的排队情况，队列 $q[i]q[i]$ 表示第 $ii$ 个小组内部的排队情况，使用数组 $in\mathrm{\_}lis[i]in\backslash \_lis[i]$ 记录第 $ii$ 个小组是否参与了排队，则：

• push x

  1. 若 $in\mathrm{\_}lis[A_x]=0in\backslash \_lis[A\_x]=0$，则说明其没有参与排队，有 $in\mathrm{\_}lis[i]=1in\backslash \_lis[i]=1$，$lis\mathrm{.}push(A_x)lis.push(A\_x)$.

  2. 随后将元素 x 放入对应的小组队列 $q[A_x]q[A\_x]$ 中，即 $q[A_x]\mathrm{.}push(x)q[A\_x].push(x)$.

• pop

  1. 输出排在队首的小组 $lis\mathrm{.}front()lis.front()$ 的队首元素，即 $q[lis\mathrm{.}front()]\mathrm{.}front()q[lis.front()].front()$.

  2. 将此元素从小组内部的队列 $q[lis\mathrm{.}front()]q[lis.front()]$ 中删除，即 $q[lis\mathrm{.}front()]\mathrm{.}pop()q[lis.front()].pop()$.

  3. 若此时小组为空，即 $q[lis\mathrm{.}front()]\mathrm{.}empty()=1q[lis.front()].empty()=1$，则将小组从小组队列 $lislis$ 中删除，即 $in\mathrm{\_}lis[lis\mathrm{.}front()]=0in\backslash \_lis[lis.front()]=0$，$lis\mathrm{.}pop()lis.pop()$.

     注意 $in\mathrm{\_}lis[lis\mathrm{.}front()]=0in\backslash \_lis[lis.front()]=0$ 和 $lis\mathrm{.}pop()lis.pop()$ 的执行顺序不能改变，否则删除队首元素后，就没有办法找回它来更新数组 $in\mathrm{\_}lisin\backslash \_lis$ 了.

代码实现

//洛谷P2776小组队列
#include<bits/stdc++.h>
using namespace std;
const int M = 305, N = 100005;
int a[N];
int in_lis[M];
queue<int>lis, q[M];
int main() {
	ios::sync_with_stdio(0); cin.tie(0);
	int n, m; cin >> n >> m;
	for (int i = 0; i < n; ++i) cin >> a[i];
	int T; cin >> T;
	while (T--) {
		string opt;
		cin >> opt;
		if (opt == "push") {
			int x; cin >> x;
			if (!in_lis[a[x]]) {
				in_lis[a[x]] = 1;
				lis.push(a[x]);
			}
			q[a[x]].push(x);
		} else {
			cout << q[lis.front()].front() << endl;
			q[lis.front()].pop();
			if (q[lis.front()].empty()) {
				in_lis[lis.front()] = 0;
				lis.pop();
			}
		}
	}
	return 0;
}

时间复杂度分析

总共有 $TT$ 次操作，每次操作不论 push 还是 pop 的时间复杂度都是 $O(1)O(1)$，故总的时间复杂度为 $O(T)O(T)$.

以下题目会在后继章节补充.

• 洛谷 P2422 良好的感觉
• 洛谷 P2629 好消息，坏消息
• 洛谷 P1714 切蛋糕

以下题目的解法已经在本节介绍过（或过于相似）

• 洛谷 P1440 求m区间内的最小值
• 洛谷 P2032 扫描

附件