GAN存在的问题
关于原始的GAN存在的问题,可以看我专栏里面GAN原理那篇文章,这篇文章主要用于记录BEGAN的原理及代码实现。
介绍
BEGAN是Google在17年3月提出的,这篇论文和GAN的最大的区别在于他可以解决传统GAN存在的模式崩溃,难以训练,难以控制生成器和判别器的平衡等问题。GAN之后出现的DCGAN,WGAN,WGAN-GP等都是使用了概率估计的方法,BEGAN的做法是不是去估计生成分布 PG和真实分布 Px的差距,而是去估计分布的误差的分布之间的差距,作者认为只要分布之间的误差分布也相近的话,也可以认为这些分布是相近的。
BEGAN的创新点
- 提出了一种新的简单强大GAN网络结构,使用标准的训练方式不加训练trick也能很快且稳定的收敛。
- 对于GAN中,生成器和判别器的平衡提出了一种均衡的概念,就是现在有一个变量可以明确指示GAN网络处于哪种均衡状态。
- 提出了一个超参数,这个超参数可以在图像的多样性和生成质量之间做均衡。
- 提出了一种收敛程度的估计,这个机制只在WGAN中出现过。论文中也说过,他们的灵感来自于WGAN。
BEGAN网络结构
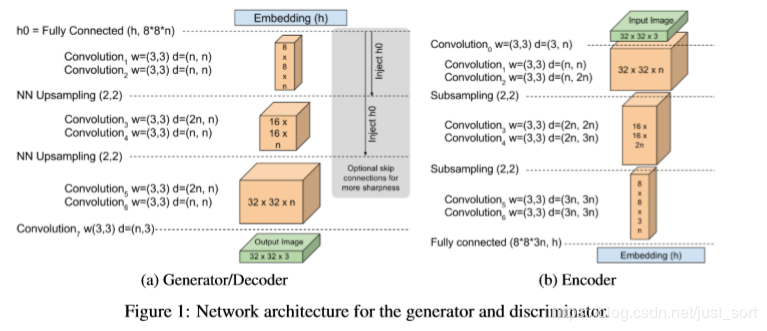 上图是BEGAN在mnist数据上设计的一个模型,借助了EBGAN的encoder-decoder作为D网络结构的思想。一共有三个网络,分别是G网络,以及D网络中的encoder和decoder。其中G网络和decoder的网络结构是一样的,这两个网络旁边灰色部分是可选的优化结构(跳跃连接和加入h0信息)。
上图是BEGAN在mnist数据上设计的一个模型,借助了EBGAN的encoder-decoder作为D网络结构的思想。一共有三个网络,分别是G网络,以及D网络中的encoder和decoder。其中G网络和decoder的网络结构是一样的,这两个网络旁边灰色部分是可选的优化结构(跳跃连接和加入h0信息)。
BEGAN的损失函数
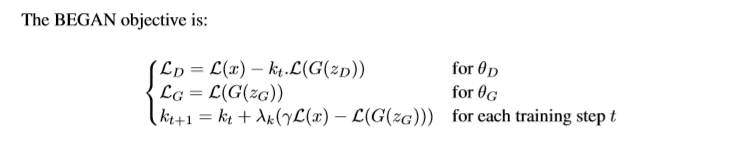
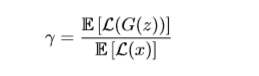 其中 L表示重构误差, L(x)=L1loss(采样而来的真实图片y和y经过D网络重构出的图片), L(G(zG))=L1loss(随机向量 zG经过decoder生成的图片和G网络生成的图片经过D网络重构出来), γ∈[0,1]是一个超参数,值越小代表生成的样本多样性越低。 λk是 kt+1的更新步长、最后论文提出了一个衡量模型收敛性的公式:
其中 L表示重构误差, L(x)=L1loss(采样而来的真实图片y和y经过D网络重构出的图片), L(G(zG))=L1loss(随机向量 zG经过decoder生成的图片和G网络生成的图片经过D网络重构出来), γ∈[0,1]是一个超参数,值越小代表生成的样本多样性越低。 λk是 kt+1的更新步长、最后论文提出了一个衡量模型收敛性的公式:
Mglobal=L(x)+∣γL(x)−L(G(zG))∣。
BEGAN的损失函数推导
L是一个自编码器的重构误差函数。我们现在假设自编码器有2个重构误差的分布函数分别是 μ1和 μ2,并用 Γ(μ1,μ2)表示 μ1和 μ2的所有肯呢个集合, m1,2为 μ1,μ2的期望。这样我们可以将Wasserstein距离定义为: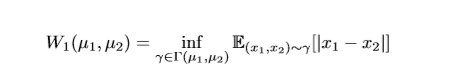 其中, x1,x2分别为从 γ=(μ1,μ2)中采样出来的两个损失函数的值,要真正优化上面的公式是不可能的,因为 Γ的样本空间太大了。但是使用Jensen不等式我们可以得到:
其中, x1,x2分别为从 γ=(μ1,μ2)中采样出来的两个损失函数的值,要真正优化上面的公式是不可能的,因为 Γ的样本空间太大了。但是使用Jensen不等式我们可以得到:
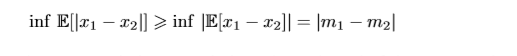 ∣m1−m2∣是Wasserstein距离的一个更低的界。 在BEGAN里,我们令 u1为 Γ(x)的分布, u2为 L(G(z))的分布。又因为最大化 ∣m1−m2∣,只有2种情况:
∣m1−m2∣是Wasserstein距离的一个更低的界。 在BEGAN里,我们令 u1为 Γ(x)的分布, u2为 L(G(z))的分布。又因为最大化 ∣m1−m2∣,只有2种情况:
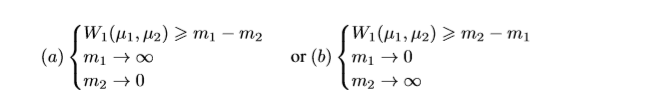 同时我们目标是让G网络生成的图片更接近真实。因此我们选择(b),于是有:
同时我们目标是让G网络生成的图片更接近真实。因此我们选择(b),于是有:
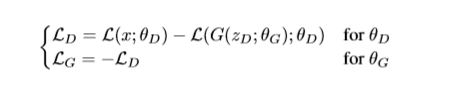 这就是BEGAN的损失函数了。为了控制G网络和D网络之间能力的平衡,以及G网络生成样本多样性和质量之间的平衡,作者还引入一开始介绍的BEGAN损失函数最终形式中的k和 γ 两个参数。
这就是BEGAN的损失函数了。为了控制G网络和D网络之间能力的平衡,以及G网络生成样本多样性和质量之间的平衡,作者还引入一开始介绍的BEGAN损失函数最终形式中的k和 γ 两个参数。
代码实现
https://github.com/artcg/BEGAN

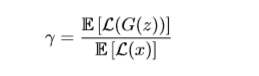
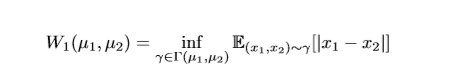
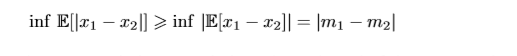
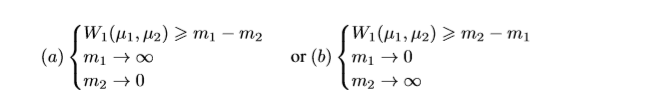
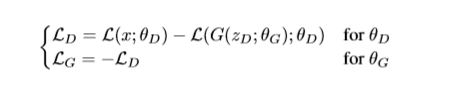



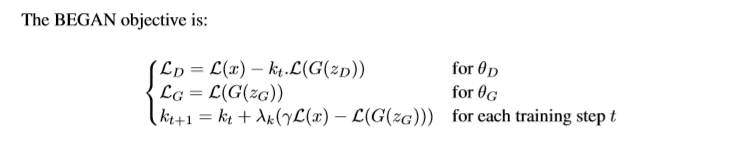

 京公网安备 11010502036488号
京公网安备 11010502036488号