前一段时间在看Selective Search【1】的论文,其前期工作就是利用Graph-Based Image Segmentation【2】的分割算法,在深入阅读论文【2】以及查阅代码之后,深深地为作者的清晰逻辑折服。在此将自己对于这篇论文的理解记录下来。后期将继续补充对Selective Search的理解。
【2】是2004年由Felzenszwalb发表在IJCV上的一篇文章,主要介绍了一种基于图表示(graph-based)的图像分割方法。图像分割(Image Segmentation)的主要目的也就是将图像(image)分割成若干个特定的、具有独特性质的区域(region),然后从中提取出感兴趣的目标(object)。而图像区域之间的边界定义是图像分割算法的关键,论文给出了一种在图表示(graph-based)下图像区域之间边界的定义的判断标准(predicate),其分割算法就是利用这个判断标准(predicate)使用贪心选择(greedy decision)来产生分割(segmentation)。该算法在时间效率上,基本上与图像(Image)的图(Graph)表示的边(edge)数量成线性关系,而图像的图表示的边与像素点成正比,也就说图像分割的时间效率与图像的像素点个数成线性关系。这个算法有一个非常重要的特性,它能保持低变化(low-variability)区域(region)的细节,同时能够忽略高变化(high-variability)区域(region)的细节。这个性质很特别也很重要,对图像有一个很好的分割效果(能够找出视觉上一致的区域,简单讲就是高变化区域有一个很好聚合(grouping),能够把它们分在同一个区域),这也是为什么那么多人引用该论文的原因吧。
对于图像分割的其他相关算法了解的不是很多,不在这里多说。大致按照原论文的格式来谈谈自己的理解。
一、图像区域的理解;
二、知识准备;
三、相关定义;
四、算法过程;
五、算法证明;
六、算法效率分析;
七、算法实现及样例。
一、图像区域的理解
在做图像分割,首先需要理解如何定义一个区域,我们人眼可以很轻松地解决这个问题,但是使用数字化语言定义就没有那么容易了。比较直观的区域划分方法有,区域的颜色,边缘,纹理。我们来看一个例子:
人眼看上图左上角区域,很容易判断出有三个区域。左半部分是灰度渐进变化的,右半部分外层灰度均匀变化,内层灰度变化较大。
当然我们也希望算法能够实现这一点,上图的例子告诉我们不能使用灰度的变化作为分割依据,也不能使用单一的灰度阈值来作为分割的评判标准。能够捕捉视觉上重要的区域(perceptually important regions)对于一个分割算法来说是非常有意义的。
人的视觉是一个非常复杂的系统,我们无法给出一个通用的区域的定义,但要是能够捕捉到视觉上重要的区域(perceptually important regions),我们就可以认为是一个非常成功的定义方式。
二、知识准备
该论文主要有两个关键点:1. 图像(image)的图(graph)表示;2. 最小生成树(Minimun Spanning Tree)。
图像(image)的图表示是指将图像(image)表达成图论中的图(graph)。具体说来就是,把图像中的每一个像素点看成一个顶点vi ∈ V(node或vertex),像素点之间的关系对(可以自己定义其具体关系,一般来说是指相邻关系)构成图的一条边ei ∈ E,这样就构建好了一个图 G = (V,E)。图每条边的权值是基于像素点之间的关系,可以是像素点之间的灰度值差,也可以是像素点之间的距离(如果是4-邻域相邻关系的话,这个权值就没意义了)。
将图像表达成图之后,接下来就是要如何分割这个图,或者这么理解,将每个节点(像素点)看成单一的区域,然后进行合并。【2】中使用最小生成树方法合并像素点,然后构成一个个区域。关于最小生成树的具体原理,请自己查看相关资料。大致意思就是讲图(Graph)简化,相似的区域在一个分支(Branch)上面(有一条最边连接),大大减少了图的边数。
三、相关定义
【2】介绍的图像(image)的图(graph)表示为G=(V,E),每个像素点代表图的一个顶点vi ∈ V ,相邻的两个像素点构成一条边(vi, vj) ∈ E,像素颜色值的差异构成边(vi, vj)的权值w((vi, vj))。相邻的像素点,可以是像素的4邻域也可以是8邻域。边之间的权值w((vi, vj))还可以通过其他的关系来定义,比如说位置(location)。在下面的讨论中,权值越小,表示像素点之间的相似度就越高,反之,相似度就越低。
接下来主要讲graph的分割,这里实现的算法与传统的图分割(Graph-Cut,可以参考【3】的系列博客,这里不再提及)还是有些不同的。这里的分割是将G = (V,E) 分割成一系列不相交的部分(component) C,每个C都构成一个子图G‘。这些子图的之间相互独立(disjoint),主要是指它们之间没有公共的点。
先介绍几个定义,用于算法的实现。
1. 分割区域(Component)的内部差(internal difference)。可以先假定图G已经简化成了最小生成树 MST,一个分割区域C 包含若干个顶点 ,顶点之间通过最小生成树的边连接。这个内部差就是指分割区域C中包含的最大边的权值。
2. 分割区域(Component)之间的差别(Difference),是指两个分割区域之间顶点相互连接的最小边的权值。
如果两个分割部分之间没有边连接,定义 Dif(C1,C2) = ∞。分割区域的差别可以有很多种定义的方式,可以选择中位置,或者其他的分位点(quantile,中位置是0.5分位点),但是选取其他的方式将会使得这个问题成为一个NP-hard问题,在后面讨论这个问题,见附录。
3. 分割区域(Component)边界的一种判断标准(predicate)。判断两个分割区域之间是否有明显的边界,主要是判断两个分割部分之间的差别Dif相对于
和
中较小的那个值MInt的大小,这里引入了一个阈值函数τ 来控制两者之间的差值。下面给出这个判断标准的定义:
其中,是指最小的分割内部差,其定义如下:
阈值函数τ 主要是为了更好的控制分割区域边界的定义。比较直观的理解,小分割区域的边界定义要强于大分割区域,否则可以将小分割区域继续合并形成大区域。在这里给出的阈值函数与区域的大小有关。
|C|是指分割部分顶点的个数(或者像素点个数),
k是一个参数,可以根据不同的需求(主要根据图像的尺寸)进行调节。
几个概念定义,用于对算法的证明:
1. 如果一个分割S,存在图(Graph)的分割区域之间,没有明显的边界,那么就说这个分割S“太精细”(too fine)。
这个定义乍看有点费解,直观地讲就是一个分割,存在这两个区域,它们之间没有明显的分界线,硬要把它们分割开来的话,有点过头,也就是说分得太细。当然对于分割来说,分割区域越小,当然就越精细了,也就 too fine。
2. 如果一个分割S,存在一个合适的调整(refinement)S’使得S不是”太精细“,那么就说这个分割S”太粗糙“(too coarse)。
这个定义的理解需要用到上面的定义,也有点费解,不过想通了就很简单。这里的调整(refinement)是指,在原有分割中的一个或多个分割区域继续往下分割。根据”太精细“(too fine)的定义,不”太精细“(not too fine)就是指每个分割区域之间都有明显的边界。那么”太粗糙“,是指存在一个调整使得存在一个不”太精细“(not too fine)的分割。简单来讲就是,分割程度的还不够(粒度还比较大),可以继续分割,这样刚开始的那个分割就是”太粗糙“(too coarse)了。
不知道上面的概念有没有把你弄糊涂,或者可能我说得还不够清楚。抛弃论文词条的束缚,可能会理解更加清楚一点,直观地讲:”太精细“(too fine),就是分割过头,导致有些区域之间没有必要分割(没有明显的边界);”太粗糙“,就分割还不够,有些区域还可以继续分割。上面定义了两种较为极端的分割,自然而然就可以导出下面的性质:
对于一个图graph来说,都存在一个分割S,既不是”太精细“(too fine)也不是”太粗糙“(too coarse)。
上面这个性质比较容易理解,首先把整个图(graph)看成一个区域,那么它肯定不”太精细“(too fine),压根就没有分割。那它是不是”太粗糙“(too coarse)呢? 如果不是,那么就可以得出上面的性质。如果是,那么我们可以将区域分割,直到它不是”太粗糙“。因为把每个顶点分割成一个区域,这个已经不能再分割了,肯定不是”太粗糙“(too coarse)。有点像连续函数的性质,一个点大于0,另一个点小于0,那么必然有一个点等于0。
四、算法过程
在了解上面的一些定义之后,我们就可以对算法过程有一个深入的了解,同时可以证明算法的可行性。

上面的算法步骤翻译成通俗的理解就是:
0. 对于图G的所有边,按照权值进行排序(升序)
1. S[0]是一个原始分割,相当于每个顶点当做是一个分割区域
2. q = 1,2,…,m 重复3的操作(m为边的条数,也就是每次处理一条边)
3. 根据上次S[q-1]的构建
。选择一条边
o[q](vi,vj),如果
vi和
vj在分割
的互不相交的区域中,比较这条边的权值与这两个分割区域之间的最小分割内部差MInt,如果o[q](vi,vj) < MInt,那么合并这两个区域,其他区域不变;如果否,什么都不做。
4. 最后得到的就是所求的分割S = S[m]
上面的过程算法过程就相当于先将图分割成一个个顶点,然后通过合并策略,将它们合并,最后得到一个既不”太精细“也不”太粗糙“的分割。
五、算法证明
引理 1 :上述步骤3中的两个通过边连接的两个互不相交的区域,如果它们不合并,这两个区域就将一直保留到最后。
很容易理解,步骤3中的边是这两个区域之间相互连接最小的边,倘若这条边不允许这两个区域合并,后面权值更大的边更加不可能使得这两个区域合并,因而这两个区域能够保留到最后。
定理 1 :通过上述算法得到的分割不是”太精细“(too fine)
初始化状态S[0]的状态,分割是最精细的。通过算法,把能合并的区域都合并了,得到的区域之间都有明显的分界线,所以不是”太精细“(too fine)
定理 2: 通过上述算法得到的分割不是”太粗糙“(too coarse)
最后的状态S[m],是能够合并的区域都合并了,不能合并的都保留了下来。如果对于留下来的任意一个区域进行分割(调整refinement),那么必然就导致这两个子区域之间没有明显的分界线,那么这个调整是”太精细“(too fine)。也就说不存在一个调整(refinement)不是”太精细“(too fine)。所以最后得到分割不是”太粗糙“(too coarse)。
定理 3: 在上述算法中,相同权值的不同边的顺序不影响最后的结果。
两条边e1,e2,涉及四个顶点,只有当涉及到三个区域是对实验结果可能有影响,这里只讨论这种情况。在分割区域A和B之间,
在分割区域B和C之间。对e1
是否导致A和B合并,以及e2是否导致B和C合并,分类讨论就可以很容易得出上述结论。
六、算法效率分析
算法是使用排序和路径压缩的并查集(a disjoint-set forest with union by rank and path compression)实现。算法耗时部分主要分为两大块:
1. 步骤0的排序,使用常用的排序算法都能够达到O(mlog(m))。
2. 步骤1-3,时间效率,
α是一个非常缓慢增长的Ackerman反函数(注,至于为什么,还没弄明白,论文上是这么说的。。。)
主要的时间都是在第二部分,α由于是一个增长非常缓慢的一个函数,所以基本上可以认为是一个常数,这也就是为什么该算法基本上能够与图像像素点数量成线性关系的原因。
七、算法实现及样例
在实现过程中,首先对图像进行一个高斯滤波,这样做可以去掉一些噪声,而又不影响图像的视觉效果。在构建图表示的过程采用四邻域点,也就是每个像素点与其周边四个像素点之间各构成一条边,边的权值通过计算颜色值的欧式距离衡量。当然也可以先在每个颜色通道进行分割,然后求它们的交,这样会使得分割效果更好(分割的更精细)。阈值函数τ 的参数
k可以根据图像大小以及需求进行调节。【2】建议对于128×128的图像
,对于320×320或更大的图像
。
下面给出的的是计算权值的一小段代码,更详细的代码内容,请查看后面上传的代码【4】。
-
static inline float diff(image<float> *r, image<float> *g, image<float> *b, -
int x1, int y1, int x2, int y2) { -
return sqrt(square(imRef(r, x1, y1)-imRef(r, x2, y2)) + -
square(imRef(g, x1, y1)-imRef(g, x2, y2)) + -
square(imRef(b, x1, y1)-imRef(b, x2, y2))); -
}
测试样例:
分割之后,不同颜色代表不同区域
附录(Appendix)
前面我们提到在定义两个分割区域差别Dif时,采用的是两个区域之间连接的最小权值的边。如果采用其他分位点,如中位值,那么寻找一个既不是”太精细“(too fine)也不是”太粗糙“(too coarse)的分割是一个NP-hard问题。
在深入讨论这个问题之前,先看一下最小比分割问题(min ratio cut problem)。
首先我们考虑最小比分割(min ratio cut)问题。假定图G = (V,E),还有一个边集合F,E中的每条边表示节点之间的容量为1,F中的每条边表示节点之间的需求为1,最小比分割问题就是求图的一个分割(A,B)使得,集合A和集合B之间的容量边数以及需求边数的比值最小。最小化这个比值是一个NP-hard问题。
在不改变最小割的情况下,将上述问题,转化成E和F互不相交的一个等价图分割问题。对于每条边(a,b),可以构建一个新的节点
ab,用边
(a,ab)和
(ab,b)替换(a,b)
。如果a
和b
在分割的同一边(A或者B),那么上述替换将不会改变原来图的比值。如果两者分在不同边(一个在A,一个在B),那么使得切割面同时这两条新边,将会有一条容量边和一条需求边(原图,两者为同一条边),依然不会改变原图的比值。
将上述问题修改为:最小比(min ration)至多为ν下分割问题。设
为通过分割面
cut(A,B)的容量边数(集合E中的边),
为通过分割
面cut(A,B)的需求边数(集合F中的边)。很容易求解得到
定义图G’ = (V,E’),其中E’ = E∪F
,E中边的权值为0,F中边的权值为 1。
引理 2:在阈值函数τ = 0和 K = 1- 1/(v+1)下,当且仅当一个图
不是作为单个分割部分时,图G有一个分割器最小比分割值至多为
ν。
证明这个引理之前,我们证明:如果图G有一个分割cut(A,B),使得最小比分割值至多为
v,那么必然存在分割{C,^C},C ⊆
A,使得分割
cut(A,B)不是太精细(too fine)。
根据之前对于”太精细“(too fine)的定义,我们只需要找到一个分割区域C使得Int(C) = 0
以及
Dif(C,^C) = 1即可。在最小比分割(min ratio cut)问题中。可以得到:如果一个图G’有个分割
,使得最小比分割值至多为
v,那么有
c/(c+d) ≥ 1/(v + 1)。
c,权值为0的边数(通过
的E中的边);
d,权值为1的边数(通过
的F中的边)。也就说通过
权值为1的边的比例至少为
1/(v + 1)。在集合A中每个分割区域C都有
Int(C) = 0。(这个是因为E中的权值为0决定的,理解这一点很关键)令C
为A中到B权值为1的边数所占比最大的分割区域,那么C到^C,权值为1边数所占比至少为
1/(v + 1)。这是因为有一条权值为1的边在
C和^C
(确切的说是C
与^C∩A
之间),将图G’分割成
与
{C,^C}比将图分割成{A,B}还要多一条权值为1的边。这就意味着在
与
之间权值为0的边的比率少于
1-1/(v+1) = K。然而对于
分位点Kth处,C
与^C
的权值是1(Dif(C,^C) = 1),那么图G的分割
S = {C,^C}不是”太精细“(too fine)。进一步,图G’
作为一个整体分割区域”太粗糙“(too coarse)了。
如果图G‘不是作为单个的分割区域,令其分割区域为S = {C1,C2,…,Cl}
,那么每一对分割区域的第Kth
分位点边的权值都是1。那么C1
与^C1 = C2∪…∪Cl与
之间的第Kth
分位点边的权值也都是1。
定理 4:在使用Kth分位点定义的Dif时,找一个分割使得既不”太粗糙“(too coarse)也不”太精细“(too fine)是一个NP-hard问题。
论文中没有深入讨论为什么是一个NP-hard问题,只是提到相应的最小比分割问题是一个NP-hard问题;另外自己对NP-hard问题了解也不是很多,暂时给不出一个很好的解释,留待以后解决吧。
【1】 Selective Search
【2】 Efficient Graph-Based Image Segmentation
【3】 关于Graph Cut的一些内容,可以查看 zouxy09的相关博客以及其他的相关资料
【4】 相关实现代码
来源:http://blog.csdn.net/surgewong/article/details/39008861




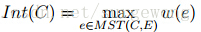
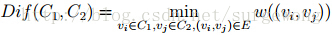
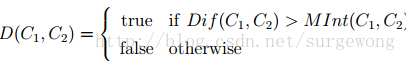
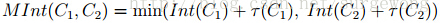
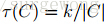

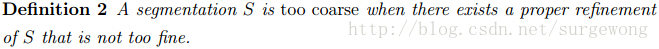
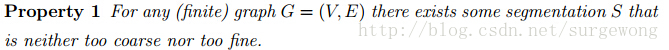

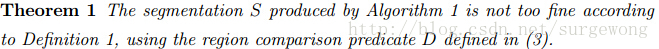
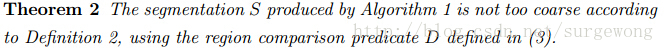
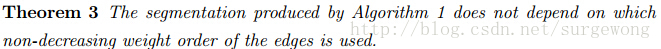


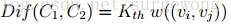
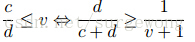
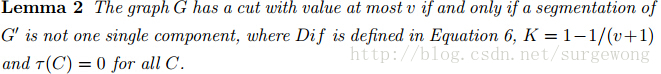
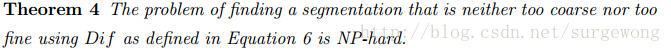

 京公网安备 11010502036488号
京公网安备 11010502036488号