
(好久没写题解了,自己打的比赛少了还是有点愧疚的,所以现在来写昨晚div2的题解)
A.Common Multiple
给定一个数组a,问你在a数组的子序列里能够构造一个y数组,y数组里面所有数字都不相同且同位置的a数组和y数组的数字相乘能相同的所有子序列中,长度最长的子序列长度为多少
由于y数组里面的数字没有大小限制,所以让a数组里面所有数字相乘就好,考虑到要y数字所有数字不相同,所以就是绕了个弯让你求数字里面有多少个不同的数字
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
int b[N];
int c[N];
void solve() {
init();
int n;
cin>>n;
int ans = n;
map<int,int>mp;
for(int i=1;i<=n;i++) {
cin>>a[i];
mp[a[i]] ++;
if(mp[a[i]] != 1) {
ans --;
}
}
cout<<ans<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}
给定一个01串,你有两个按钮,一个是0一个是1,按哪个就会输出一个字符,每按一次算一次操作次数,同时如果你的手指在0按钮上,移动到1按钮上算一次操作次数,反之亦然。但现在你有一次机会可以选定一个子串将其反转,问你输出这个01串最少需要次数
手指初始在0位置
手指初始在0位置,我们就当作前面接了个连续的0的段,不难发现,无论怎么操作最多只会让操作次数-2。
我们将连续的0和连续的1看作同一段,不难发现,我们可以-2的情况是 0 - 1 - 0 - 1 以及 1 - 0 - 1 - 0,将中间两段反转便可-2,但注意由于前面接了一段0,所以有第二种情况必定有第一种情况,只需要找第一种情况便可。
然后是-1的情况,-1的情况无非就是前面或者后面的一段没有了,但是我们找第一种情况,并且前面接了一段0,所以只要后面没有接了一段1就是-1的情况
剩下的就是0的情况
所以这里可以用三个变量来记录是否找到第一段中的第二段,第三段,第四段(第一段是已经有了的),然后分类讨论就好了
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
int b[N];
int c[N];
void solve() {
init();
int n;
cin>>n;
string s;
cin>>s;
char now = '0';
int ans = n;
int sign1=0;
int sign2=0;
int sign3=0;
for(int i=0;i<n;i++) {
if(s[i] != now) ans++,now = s[i];
if(s[i] == '1') {
if(!sign1) sign1=1;
else if(sign2 && !sign3) sign3=1;
}
if(s[i] == '0') {
if(sign1 && !sign2) sign2 = 1;
}
}
if(!sign1) cout<<ans<<"\n";
else if(sign1 && !sign2) cout<<ans<<"\n";
else if(sign2 && !sign3) cout<<ans-1<<"\n";
else cout<<ans-2<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}
给定一个数组,你要判断是否能将其按原本的顺序分为三个子数组,使得这三个子数组的中位数的中位数小于等于k。
注意在本题目中,中位数的定义是m / 2向上取整,其中m为求中位数的数组长度
首先第一:三个子数组的中位数的中位数要小于等于k,那么这三个子数组的中位数至少有两个小于等于k
第二:前面或者后面的子数组肯定要有一个是满足条件的
第三:如果前面满足条件之后,先看能不能带走一个大于k的数贪心一下,然后遍历剩下两个子数组的分界线即可
第四:判断是否满足条件只需要知道这段的长度以及有多少个小于等于k的数字即可
由此可见:我们只需要看从前面第一个数字遍历,找到第一个满足条件的位置,然后贪心看能否带走一个大于k的数字,然后遍历剩下两个子数组的分界线,然后将数组反过来再进行一次操作即可
看起来是不是超级麻烦,其实有很多地方可以优化,可以参考我的代码
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
int b[N];
int pre1[N];
int pre2[N];
void solve() {
init();
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++) {
cin>>a[i];
b[n - i + 1] = a[i];
}
for(int i=1;i<=n;i++) {
pre1[i] = pre1[i-1];
pre2[i] = pre2[i-1];
if(a[i] <= k) pre1[i]++;
if(b[i]<=k) pre2[i]++;
}
int zhi1=0;
int zhi2=0;
for(int i=1;i<=n;i++) {
if(!zhi1) {
if(pre1[i] >= i/2 + i % 2) zhi1 = i;
}
if(!zhi2) {
if(pre2[i] >= i/2 + i % 2) zhi2 = i;
}
}
if(zhi1 % 2 && a[zhi1 + 1] > k && n - zhi1 > 2) zhi1++;
if(zhi2 % 2 && b[zhi2 + 1] > k && n - zhi2 > 2) zhi2++;
//cout<<zhi1<<" "<<zhi2<<"\n";
if(zhi1) {
int sign = 0;
for(int i=zhi1+1;i<n;i++) {
int len1 = i - zhi1;
int len2 = n - i;
if(pre1[i] - pre1[zhi1] >= len1/2 + len1%2 || pre1[n] - pre1[i] >= len2/2 + len2 % 2) {
sign = 1;
break;
}
}
if(sign) {
cout<<"YES\n";
return ;
}
}
if(zhi2) {
int sign = 0;
for(int i=zhi2+1;i<n;i++) {
int len1 = i - zhi2;
int len2 = n - i;
if(pre2[i] - pre2[zhi2] >= len1/2 + len1%2 || pre2[n] - pre2[i] >= len2/2 + len2 % 2) {
sign = 1;
break;
}
}
if(sign) {
cout<<"YES\n";
return ;
}
}
cout<<"NO\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}
首先有一数组a,有两种操作,第一种操作会删去所有不是局部最小值的数字,第二种操作会删去所有不是局部最小值的数字。这两种操作会交替进行,a[i]表示第i个数字在第几次操作的时候被删去,a[i]=-1表示第i个数字没有被删去
可以证明操作次数是logn以内
你需要构造一个排列使得p排列和a数组符合条件、
保证一定有满足条件的排列
局部最小值和局部最大值的定义如下:
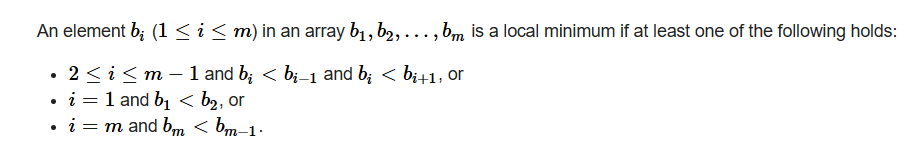
第一:要的是排列,说明每个数字都不一样
第二:由于每个数字都不一样,所以相邻的两个数肯定至少有一个会被删掉
第三:对于构造题,并且还保证一定有解的情况,那么肯定有某种通解,某种规律,按照这个规律不断填就好
从以上三点我们可以guess出一种情况就是对于第一种情况我们尽可能填已有的最大值,第二种情况我们尽可能填已有的最小值,但是要注意没有被删去的数字在中间的情况,要保证没有被删去,就要让在第一次操作的时候是局部最小值,在第二次操作的时候是局部最大值
如果按照上面的填数方法可以知道,最后剩下的数将会比所有第一次操作的数字小,比所有第二次操作的数字大,所以我们完全可以将数组按照最后剩下数字的位置分为两边然后进行填数操作
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define lowbit(x) x&(-x)
const int MOD=1e9+7;
const int N=1000100;
int a[N];
int ans[N];
void solve() {
init();
int n;
cin>>n;
int maxtime = 0;
for(int i=1;i<=n;i++) {
cin>>a[i];
ans[i]=0;
maxtime = max(a[i],maxtime);
}
int l=1,r=n;
for(int i=1;i<=maxtime;i++) {
vector<int>b[2];
int sign = 0;
for(int j=1;j<=n;j++) {
if(a[j] == -1) {
sign = 1;
continue;
}
if(a[j] == i) b[sign].push_back(j);
}
ranges::reverse(b[1]);
for(auto pos : b[0]) {
if(i & 1) ans[pos] = r --;
else ans[pos] = l ++;
}
for(auto pos : b[1]) {
if(i & 1) ans[pos] = r--;
else ans[pos] = l++;
}
}
for(int i=1;i<=n;i++) {
if(ans[i] == 0) {
ans[i] = l;
}
cout<<ans[i]<<" ";
}
cout<<"\n";
}
signed main() {
//ios::sync_with_stdio(false);
//cin.tie(0);
//cout.tie(0);
//for(int i=1;i<=cnt;i++) cout<<prime[i]<<"\n";
int t=1;
cin>>t;
while(t--) {
solve();
}
return 0;
}




 京公网安备 11010502036488号
京公网安备 11010502036488号