[HDU3544] Alice’s Game
题意:
给n块巧克力,第i块是 ni∗mi,Alice只能垂直切,切成 A∗m和B∗m,并且 A+B=n,Bob只能横切,只能切成 A∗n和B∗n,并且 A+B=m
分析:
语言表达能力有限
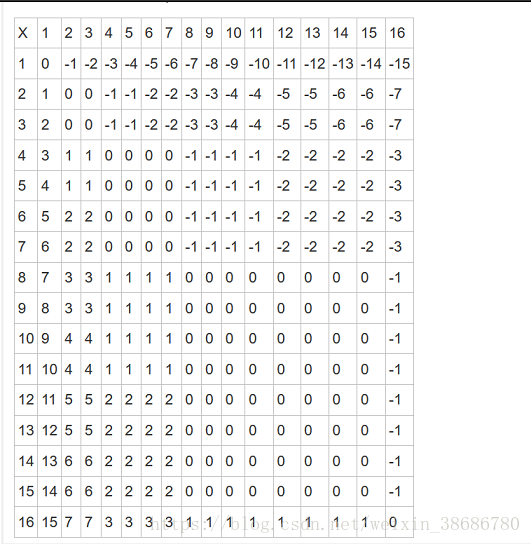
我们采取 HP(n,m)表示 n∗m的矩形对Alice的可切割次数的贡献,负数代表对Bob的贡献,如果所有 ∑HPi>0 ,Alice必赢, ∑HPi<=0,Bob(必赢)
对于HP(i,j) 的计算我们有如下法则
1. n∗1 的矩形贡献为n-1
2. 1∗m 的矩形贡献为-(m-1)
3. 2∗2,3∗3,4∗4..n∗n的矩形对HP的贡献为零,因为如果你首先下手切,都会给对手更多的机会,如果你能赢,你不会切这个,如果你输,那么切了这个你还会输。
4. 对于 2∗3,3∗2,5∗4...,的矩阵来说与3的状况相同,对答案的贡献都是0,首先下手都会给对手更多的机会
5. 贡献为零的有什么规律呢,我们发现原来是它们是 2k<=n<2k+1&& 2k<=m<2k+1
6. n∗2 的矩形对于Alice来说有贡献,我们每一次可以选择都切成 2∗2,3∗2的矩形,这样不会给对手机会,自己还可以增加一次切的机会,Bob也不会傻到切这个矩形,这样会给Alice更多机会,所以 n∗2的矩形,Alice 可以切 n/2−1 次
这个时候可以总结一下规律:
- 我们每一次切,都会切成 HP(i,m)=0,HP(n−i,m)>=0的 两块, HP(n,m)=HP(n−i,m)+1,递归下去 HP(n−i−j,m)=HP(n−i−j,m)+1,直到 HP(n−i−j....,m)=0,这怎么计算呢
- 我们知道 HP(n,m)=0 当且仅当 2k<=n<2k+1&& 2k<=m<2k+1
- 那么就有 HP(n,m)=n/(2k)−1
参考代码
初级
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL solve(LL x,LL y)
{
LL t = 1;
while(t*2 <= y)
t <<= 1;
return x/t;
}
int main()
{
int T,n;
scanf("%d",&T);
for(int kase = 1; kase <= T; ++kase)
{
scanf("%d",&n);
LL x,y;
LL sum=0;
for(int i=1; i<=n; i++)
{
scanf("%lld%lld",&x,&y);
if(x > y) sum += solve(x,y)-1;
else sum -= solve(y,x) -1;
}
printf("Case %d: ",kase);
if(sum > 0) puts("Alice");
else puts("Bob");
}
return 0;
}
简化
下面这个版本就是大家在其他博客上看到的答案了
就是不停的对两边除以2,其实原理和 n/2k−1相同
#include <cstdio>
typedef long long LL;
int main()
{
int T; scanf("%d", &T);
for(int kase = 1; kase <= T; kase++)
{
int n; scanf("%d", &n);
LL a = 0, b = 0;
while(n--)
{
int x, y;
scanf("%d%d", &x, &y);
while(x > 1 && y > 1) { x >>= 1; y >>= 1; }
if(y == 1) a += (LL)x - 1;
if(x == 1) b += (LL)y - 1;
}
printf("Case %d: %s\n", kase, a > b ? "Alice" : "Bob");
}
return 0;
}




 京公网安备 11010502036488号
京公网安备 11010502036488号