快速傅里叶变换（前）

快速傅里叶变换 FFT，也就是 Fast Fourier Transform，是利用离散傅里叶变换（DFT）的高效、快速计算方法的算法统称。对于一个 OIer，FFT 最大的用处是用来加速多项式乘法。其本质是以 $O (n l g n)$ 的时间复杂度将点值表示法与系数表示法相互转换。

这篇文章没有成堆的空洞乏味的公式推导，以简洁易懂的数形结合思想解释 FFT 算法。当然，没有严格的证明也是缺点之一。

多项式的表示

多项式的表示主要有两种，第一种是最常见的系数表示法。将每个项的系数写在一起组成一个向量，缺少的项就补 $0$ ，顺序最好按照次数的大小从小到大，因为这样可以与数组的下标对应起来。

例如多项式 $x^{2} + 2 x + 4$ 写成数组 $[4, 2, 1]$ 。

第二种是，任意 $k$ 次的多项式都可以用 $k + 1$ 个点唯一确定。这是很好理解的， $k$ 次多项式有 $k + 1$ 个系数，也就是 $k + 1$ 个未知数。若有 $k + 1$ 个关于他们的方程，就能够全部解出来。

例如多项式 $x^{2} + 2 x + 4$ 就可以用点值 $(0, 4), (1, 6), (2, 12)$ 表示出来。

分别考虑两种表示法的多项式乘法。对于系数表示法，多项式乘法是基于乘法分配律的 $O (n^{2})$ 算法，很难再做优化。而对于点值表示法，假设这两个多项式是 $n$ 次与 $m$ 次的，那么结果的多项式就需要 $n + m + 1$ 个点值来表示。如果我们已经有了前两个多项式每个的 $n + m + 1$ 个点值（要选一样的 $x$ ），那么最后结果的点值只需要将这些点值的值一一乘起来就行了，复杂度是 $O (n)$ 。

例如多项式 $x^{2} + 2 x + 4$ 与 $2 x^{2} + x + 3$ 相乘，结果是 $4$ 次的多项式，可以用 $5$ 个点值表示出来。所以为 $x^{2} + 2 x + 4$ 与 $2 x^{2} + x + 3$ 每个式子找到 $5$ 个点值：

$(0, 4), (1, 6), (2, 12), (3, 19), (4, 28)$
$(0, 3), (1, 6), (2, 13), (3, 24), (4, 39)$

结果就是： $(0, 12), (1, 36), (2, 156), (3, 456), (4, 1092)$

虽然点值法的乘法很快，但大部分情况题目给出的和我们需要的都是系数表示法的多项式，并且系数表示到点值表示的转换是 $O (n^{2})$ 的复杂度，和分配律是一样的。我们需要一种能快速转换点值表示法和系数表示法的算法，而这正是 FFT 的用处。

计算点值

在讲 FFT 之前还需要思考一下其中的原理。速度不可能平白无故变快，一定是用什么方法减少了运算量。比如分治就是将本来需要计算两次的问题分解成两个只要计算一次的子问题，并且子问题是可以通过某种对称性互相转换的，这样每次递归就可以减少一半的运算量。FFT 也运用了分治思想。

既然是分治，就需要找到点值计算中的对称性。有没有哪些特别的点值我们只需要计算一个就能直接知道另一个？有，对于奇函数和偶函数，计算一个点值后，其相反数的值就可以瞬间得到。

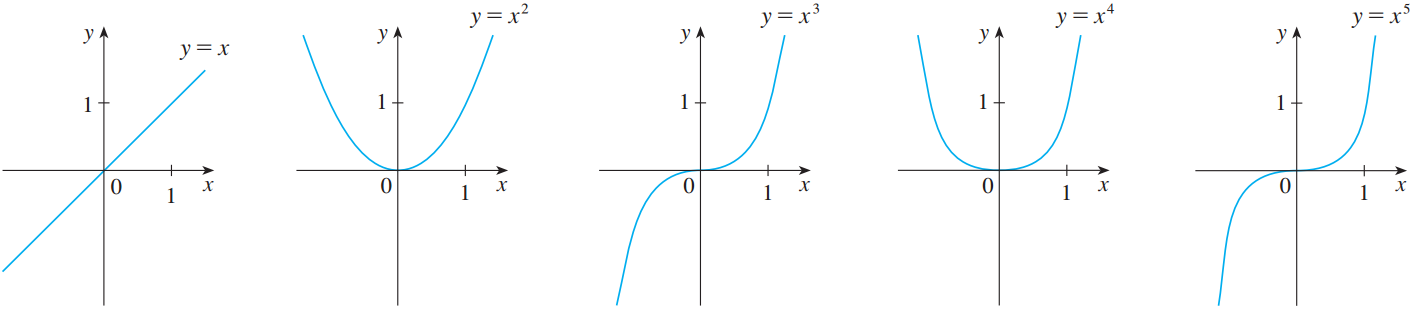
但大部分多项式都没有奇偶性，所以我们要加工一下。分离多项式 $f (x)$ 中的偶次项和奇次项，偶次项组成的多项式写作 $e v e n (x)$ ，奇次项的写作 $o d d (x)$ ，提取公因式后能写成 $e v e n (x^{2})$ 和 $x \times odd(x^2)$ 。于是 $f(x)=even(x^2)+x \times odd(x^2)$ 。

例如有多项式 $f (x) = x^{3} + 2 x^{2} + 3 x + 4$ ，那么 $e v e n (x^{2}) = 2 x + 4$ ， $o d d (x^{2}) = x + 3$ ， $f(x)=even(x^2)+x \times odd(x^2)$ 。

加工了以后，因为一个数的平方和其相反数的平方是一样的，所以 $f(-x)=even(x^2)-x \times odd(x^2)$ 。如此，计算一个点值时，算出 $e v e n (x^{2})$ 和 $o d d (x^{2})$ 的值就能得到答案了，其相反数的值也只需要将 $o d d (x^{2})$ 取反就能得到。因为点值可以随意选择，所以我们一定会选择正负成对出现的点，因为这样我们就能用上面的公式减少一半的计算量，因为算出正的一半，负的一半也知道了。

例如计算多项式 $f (x) = x^{3} + 2 x^{2} + 3 x + 4$ 的 $2$ 个点值，我们选择 $x=\pm1$ 。先算 $x = 1$ ， $e v e n (1^{2}) = 6$ ， $o d d (1^{2}) = 4$ ，那么 $f(1)=6+1\times4=10$ 。再算 $x = - 1$ ，这时我们不需要再算 $e v e n (x^{2})$ 与 $o d d (x^{2})$ 了，只要变加为减， $f(-1)=6-1\times4=2$ 。

不过这样也只是常数优化，没有任何用。细心的读者可能已经发现了，计算 $e v e n (x^{2})$ 和 $o d d (x^{2})$ 也是求点值的问题，我们是不是可以用同样的方法优化呢？如果可以的话分治就成立了，计算点值的时间复杂度将变成 $O (n l g n)$ 。可惜这个分治是不成立的，因为只有在第一次计算中我们可以随意选择点，选择那些正负成对的点，第二次计算的时候已经平方了，这时就不可能还是正负成对的了。

例如计算 $x = 1, 2, - 1, - 2$ 上的点值，这时是正负成对的，我们只需要计算 $x = 1, 2$ 就能知道 $x = - 1, - 2$ 的值。但继续计算 $e v e n$ 和 $o d d$ 中 $x = 1^{2}, 2^{2}$ 的点值时，就不能继续分治了，因为此时的 $1$ 和 $4$ 不再是正负成对了。

单位根

可以随意选择点值是幸运的，甚至可以不在实数范围内找，因为实数中没有满足平方前符号相同，平方后变成正负成对的一组数，但复数中存在。

复数的一般形式为 $a + b i$ ，其中 $i^{2} = - 1$ ， $a$ 和 $b$ 均为实数。当 $b = 0$ 时，这个复数就是实数，当 $a = 0$ 时，这个复数是纯虚数。复数支持加、减、乘、除运算，也支持实数内的运算法则，例如分配律、结合律。复数 $a + b i$ 的共轭数为 $a - b i$ ，也就是含 $i$ 的项取反。

复平面对于复数就如数轴对于实数，不同的是这是个二维平面，平面上的任意坐标 $(a, b)$ 代表了复数 $a + b i$ 。复平面实际上就是数轴多了个与其垂直的虚轴，是实数领域的拓展。

有了复平面以后，我们可以将任意复数表示成从原点指向其坐标的一个向量。向量的幅角为该向量与正实轴之间划过的角度。向量的模长是坐标到原点的距离。

这样，复数的加法和乘法就能用向量的运算表示出其几何意义了。加法就是向量中的平行四边形法则，头尾相接然后连线。乘法则是幅角相加，模长相乘。

如坐标系中一样，复平面上也有单位圆——以原点为圆心， $1$ 为半径。

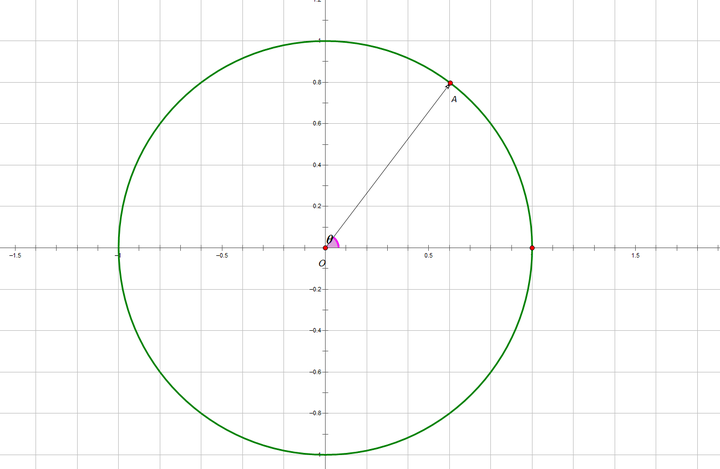
在圆上作 $n$ 个点将单位圆等分成 $n$ 份（以单位圆与实轴正半轴的交点为一个等分点）。然后以原点为起点，圆上的这 $n$ 个等分点为终点，作出 $n$ 个向量。其中幅角最小的那个的向量被称为 $n$ 次单位根，记做 $\omega_n^1$ ，其余的向量分别为 $\omega_n^2$ ， $\omega_n^3$ ， $\dots$ ， $\omega_n^n$ 。

单位根的代数意义是 $x^{n} = 1$ 的解，一定会有 $n$ 个解，这 $n$ 个解正是 $\omega_n^1$ ， $\omega_n^2$ ， $\omega_n^3$ ， $\dots$ ， $\omega_n^n$ ，其中实数解只有 $1$ ，有时有 $- 1$ ，其余都是复数解。

为什么 $x^{n} = 1$ 的解会这么规律的排布在单位圆上呢？回忆我们刚才提过的复数乘法的几何意义，又因为单位圆上的向量模长都为 $1$ ，所以模长相乘后不会变，只有幅角相加了。因为幂运算来自于乘法所以也可以这样解释，一个单位圆上的向量的 $n$ 次方就是将其幅角乘 $n$ 。于是求解 $x^{n} = 1$ 就转换成了找到角度 $\theta$ ，使 $\theta \times n=k\times360^\circ$ （ $k$ 为任意整数，也就是 $360^\circ$ 的倍数），因为 $1$ 的向量幅角为 $0^\circ$ 也就是 $360^\circ$ 。

下面举些例子。很明显， $\theta=0^\circ$ 就是一个解，这与实际是相符的，因为 $x = 1$ 确实是一个解。当 $\theta=180^\circ$ 也就是 $- 1$ 的向量的幅角时，只有当 $n$ 是偶数时才是方程的解，不然结果为 $- 1$ ，因为 $n$ 若是奇数那 $n\times\theta$ 就不是 $360^\circ$ 的倍数了，就不能落在 $1$ 的向量上了。这与实际也是相符的，例如 $x^{4} = 1$ 有 $x = - 1$ 的解，而 $x^{3} = 1$ 没有。

所以除 $1$ 以外的幅角最小的那个解一定是以 $\frac{360^\circ}{n}$ 为幅角， $1$ 为模长的向量，这个解也就是单位根 $\omega_n^1$ 。同时，单位根幅角的倍数也一定是方程的解，因为当 $\theta \times n=360^\circ$ ，就有 $k\times \theta \times n=k\times360^\circ$ ，也是 $360^\circ$ 的倍数，也能在 $n$ 次幂后会落在向量 $1$ 上。所有以单位根幅角的倍数为幅角，模长为 $1$ 的向量一共有 $n$ 个，那正是单位圆上的 $n$ 等分点为终点的向量。