题目一从尾到头打印链表

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/cong-wei-dao-tou-da-yin-lian-biao-lcof/

1.描述

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

2.示例

示例 1：

输入：head = [1,3,2]
输出：[2,3,1]

解法一迭代+辅助栈

解题思路

看到题不难想到最简单的办法就是借助一个辅助栈，顺序遍历将节点值入栈，然后再依次出栈，就能实现倒序打印。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        vector<int> ans;//存储答案
        if(head == nullptr) return ans;//如果节点为空，输出空数组
        stack<int> tempAns;//辅助栈
        ListNode* temp = head;
        //顺序遍历，将节点值压栈
        while(temp != nullptr){
            tempAns.push(temp->val);
            temp = temp->next;
        }
        while(!tempAns.empty()){//出栈直至栈为空
            ans.push_back(tempAns.top());
            tempAns.pop();
        }
        return ans;//返回答案
    }
};

复杂度分析

时间复杂度： O(m)。m为链表长度，遍历链表和出栈各需要O(m)时间。
空间复杂度： O(m)。辅助栈的空间消耗。

解法二递归

解题思路

也可以借助递归一直递推至链表尾部再层层回溯以实现反向输出。这样的方法代码简洁，但是调用函数时间消耗较大。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        if(head==nullptr) return ans;//如果头结点为空，返回空数组
        reversePrint(head->next);//递推
        ans.push_back(head->val);//回溯，持续存值
        return ans;//返回答案
    }

    vector<int> ans;
};

复杂度分析

时间复杂度： O(m)。递归的时间消耗
空间复杂度： O(m)。递归的空间消耗。

题目二反转链表

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/fan-zhuan-lian-biao-lcof/

1.描述

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

2.示例

示例 1：

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

解法一迭代+辅助栈

解题思路

参考题目一，我们可以写出迭代+辅助栈的版本。首先遍历链表将节点存入辅助栈，然后再倒序遍历辅助栈并将每个节点的next指针指向前一个节点。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head==nullptr || head->next==nullptr) return head;//如果头结点为空或者只有一个节点，返回其本身
        vector<ListNode*> aid;//辅助栈
        while(head!=nullptr){//顺序遍历链表并压栈
            aid.push_back(head);
            head = head -> next;
        }
        ListNode* ans = new ListNode(0);//假头节点
        ListNode* temp = ans;
        for(int i = aid.size()-1; i >= 0; --i){//倒序遍历节点并修改next指针
            temp -> next = aid[i];
            temp = temp -> next;
        }
        temp -> next = nullptr;
        return ans->next;//返回翻转后的链表头节点
    }
};

复杂度分析

时间复杂度： O(m)。m为链表长度，遍历链表和倒序遍历修改next指针各需要O(m)时间。
空间复杂度： O(m)。辅助栈的空间消耗。

解法二迭代+三指针

解题思路

解法一的辅助栈耗费了大量空间，实际上只需要使用三指针即可。
我们使用指针prePtr，curPtr，nextPtr分别指向上一节点，当前节点，下一节点。初始时，prePtr，curPtr，nextPtr分别为nullptr，head以及head->next，然后顺序遍历链表，将curPtr指向节点的next指针修改，使其指向prePtr指向的节点，之后更新三个指针，使其分别后移以为。
遍历完成后，返回当前curPtr即为答案。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head==nullptr || head->next==nullptr) return head;//若头结点为空或只有一个节点，直接返回其本身
        ListNode* prePtr = nullptr;//上一节点
        ListNode* curPtr = head;//当前节点
        ListNode* nextPtr = head->next;//下一节点
        while(nextPtr != nullptr){//依次遍历翻转
            curPtr -> next = prePtr;
            prePtr = curPtr;
            curPtr = nextPtr;
            nextPtr = nextPtr -> next;
        }
        curPtr -> next = prePtr;
        return curPtr;//返回答案
    }
};

复杂度分析

时间复杂度： O(m)。遍历链表的时间消耗。
空间复杂度： O(1)。只需常数个额外变量即可。

解法三递归

解题思路

除此之外，我们还可以使用递归方法解决本题。一般来说递归的代码比较简洁，就是有的地方不容易想。
这里再提供递归版本代码，供大家加深对递归的理解。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head==nullptr) return head;
        ListNode* temp = head -> next;
        head -> next = ans;
        ans = head;
        reverseList(temp);
        return ans;
    }
    ListNode* ans = nullptr;
};

复杂度分析

时间复杂度： O(m)。递归的时间消耗
空间复杂度： O(m)。递归的空间消耗。

题目三复杂链表的深拷贝

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/fu-za-lian-biao-de-fu-zhi-lcof/

1.描述

给你一个长度为n的链表，每个节点包含一个额外增加的随机指针random，该指针可以指向链表中的任何节点或空节点。
构造这个链表的深拷贝。深拷贝应该正好由n个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的next指针和random指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点。
例如，如果原链表中有X和Y两个节点，其中X.random-->Y。
那么在复制链表中对应的两个节点x和y，同样有x.random-->y。
返回复制链表的头节点。
用一个由n个节点组成的链表来表示输入/输出中的链表。每个节点用一个[val, random_index]表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从0到n-1）；如果不指向任何节点，则为null。
你的代码只接受原链表的头节点head作为传入参数。

2.示例

示例 1：

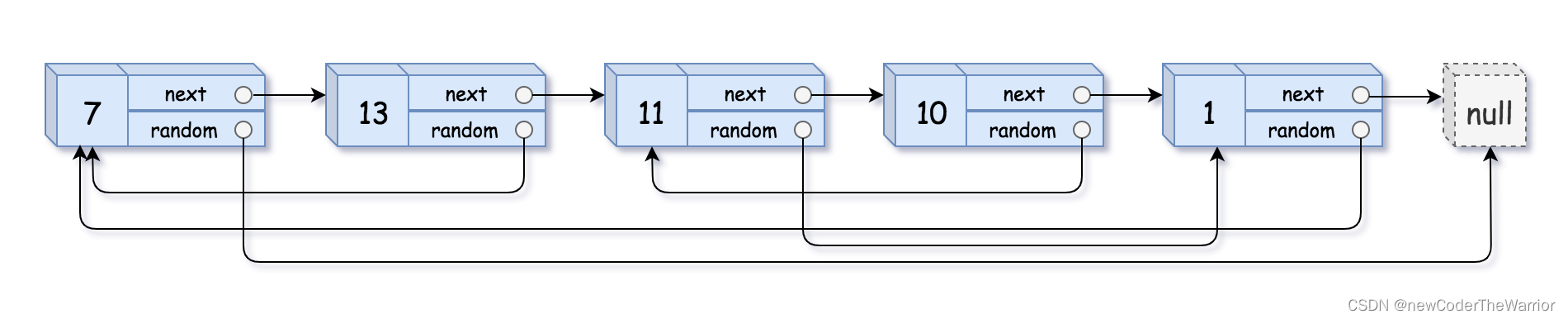
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例2

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

示例 4：

输入：head = []
输出：[]
解释：给定的链表为空（空指针），因此返回 null。

解法一暴力遍历

解题思路

可以立马想到的暴力方法就是遍历链表，使用双指针对旧链表和新链表进行同步，先创建random指针指向全为空的新链表；然后对新链表的每个节点，使用上一步的双指针同步方法再次遍历旧链表找到正确的random指向。

代码

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head == NULL || head->next == NULL)//若头结点为空或只有头结点
        {
            if(head == NULL)//如果头结点为空
            {
                return NULL;//则直接返回头结点
            }
            else//如果只有头结点
            {
                Node* NewHead = new Node(0);//新链表的头结点
                NewHead->val = head -> val;//将头结点进行复制
                NewHead -> next = NULL;//因为只有一个节点，next指向NULL
                if(head -> random == head)
                {
                    NewHead -> random = NewHead;
                }
                else
                {
                    NewHead -> random = NULL;
                }
                return NewHead;
            }
        }
        else//如果不只头结点
        {
            vector<int> randomPosition;//新建一个数组，用于记忆各个节点random指针的指向节点，俩数字一组
                                       //例如1 31就代表第一个节点的random指向31节点，25 67就代表节点25
                                       //的random指向67节点
            Node* NewHead = new Node(0);//新链表的头结点
            Node* Index = head;//采用双指针技术，这个旧链表哨兵指向原链表的当前节点
            Node* newIndex = NewHead;//这个指针指向新链表的当前节点
            NewHead->val = head -> val;//将头结点进行复制
            NewHead -> next = NULL;//因为只有一个节点，next指向NULL
            NewHead -> random = NULL;//random节点之后统一修改，因为现在新链表还未成型
            Index = Index -> next;//头结点复制完毕，旧链表哨兵向后位移指向下一个节点
            Node* positionOfRandom = NULL;//用来遍历旧链表确定random指向的游标
            if(head -> random == NULL)//如果旧链表头结点的random指向NULL
            {
               // NewHead -> random = NULL;//则新链表头结点random也指向NULL
                randomPosition.push_back(1);//1入数组，表示这是第一个节点
                randomPosition.push_back(0);//0入数组，表示该节点的random指针指向null
            }
            else//如果头节点random指向不为空，寻找头结点random指向位置
            {
                randomPosition.push_back(1);//1入数组，表示这是第一个节点
                int flag = 1;//用来记录random指向节点位置
                positionOfRandom = head;//游标指向头节点
                while(positionOfRandom != head -> random)//游标持续移动直到找到random指向位置
                {
                    flag++;
                    positionOfRandom = positionOfRandom -> next;
                }
                randomPosition.push_back(flag);//记录位置的整数入数组
            }
            int count = 1;//记录做到第几个节点了
            while(Index != NULL)//每复制完一个节点旧链表哨兵向后位移一个节点，直到全部复制完毕
            {
/***************进行节点复制工作************************************************/
                count++;//处理的节点数+1
                Node* temp = new Node(0);//新建一个节点
                temp -> next = NULL;//先将next指向空
                temp -> random = NULL;//先将random指向空
                temp->val = Index->val;//将旧节点的值复制过来
                newIndex->next = temp; //将新建节点链到新链表尾部

/**************确定该节点random指向****************************************/
                randomPosition.push_back(count);//count入数组，表示这是第count个节点
                if(Index -> random == NULL)//如果旧链表该结点的random指向NULL
               {
                randomPosition.push_back(0);//则用0记录新链表该节点random也指向NULL
               }
            else//如果旧链表该节点random指向不为空，寻找该结点random指向位置
            {
                int flag = 1;//用来记录random指向节点位置
                positionOfRandom = head;//游标指向头节点
               // Node* nonius = head -> random;
                while(positionOfRandom != Index -> random)//游标持续移动直到找到random指向位置
                {
                    flag++;
                    positionOfRandom = positionOfRandom -> next;
                }
                randomPosition.push_back(flag);//记录位置的整数入数组
            }

                Index = Index -> next;//处理完一个节点后俩游标向后位移一个位置
                newIndex = newIndex -> next;                 
            }

/***********根据之前建立的辅助数组完成random指向工作*************************************/
            //该步骤同样采用双哨兵技术
            newIndex = NewHead;
            for(int i = 0, j = 2; i < count; i++, j = j + 2)
            {
                if(randomPosition[j-1] == 0)
                {
                    newIndex -> random = NULL;
                }
                else
                {
                    positionOfRandom = NewHead;
                    for(int k = 0; k < randomPosition[j-1]-1; k++)
                    {
                        positionOfRandom = positionOfRandom -> next;
                    }
                 newIndex -> random = positionOfRandom;
                }
                newIndex = newIndex -> next;
            }
            return NewHead;
        }
    }
};

复杂度分析

时间复杂度： O(m²)。m为链表长度，建新链表和修改random指针的时间消耗分别为O(m)和O(m²)。
空间复杂度： O(1)。只需要常数个额外变量。

解法二递归+哈希表

解题思路

对于普通链表的深拷贝，我们只需要顺次遍历然后新建对应节点就可以了。但本题的难点在于，我们新建一个节点并给random指针确定指向时，它应该指向的那个节点可能还不存在。于是我们可以在新建一个节点时，递归的新建他的后继节点和random指针指向的节点。为了防止重复新建节点，我们使用哈希表标记该节点是否已有，如果有直接取用该节点，如果没有，则新建它。
递归代码通常比较简洁，但是有的递归较难以理解，需要多加练习，多读代码，以加深理解。

代码

/*Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/
class Solution {
private:
    unordered_map<Node*, Node*> created;//已建节点
public:
    Node* copyRandomList(Node* head) {
        if(head==nullptr) return head;//如果该节点为空，返回其本身
        if(!created.count(head)){//如果该节点未建立
            Node* temp = new Node(head->val);//新建该节点
            created[head] = temp;//标记该节点已建立
            temp -> next = copyRandomList(head->next);//递归建立其后继节点
            temp -> random = copyRandomList(head->random);//递归建立其random指针指向的节点
        }
        return created[head];//返回新链表
    }
};

复杂度分析

时间复杂度： O(m)。递归建立新链表的时间消耗。
空间复杂度： O(m)。哈希表的空间消耗。

解法三迭代 + 哈希表

解题思路

除了递归+哈希外，本题还可以使用迭代+哈希的方式解决，该方法相较于上一方法更好理解。
与上一方法不同的是，我们只关注当前节点random指针应指向的节点是否存在，并不关注当前节点的random指针应该指向的节点的random指针应指向的节点存不存在，也即不会直接递归创建一条链路上的全部节点（上一方法中，只要random指针指向的节点不存在，就会递归创建。），如果不存在，创建之，并标记旧链表中对应节点的新节点已创建。
具体的，我们使用pre指针指向上一个节点，cur指针指向当前工作节点，初始时pre指向一个新建的假头节点，cur指向旧链表头节点。我们从头节点开始依次遍历各个节点，首先查表判断该节点是否已存在，如果已存在，直接取用之，将pre指针指向的节点的next指针指向已新建本节点，否则创建之。之后判断其random指向是否为空或者已存在，已存在则调用之，不存在则创建之，并将本节点random指针指向它。最后更新cur指针指向本节点的下一节点继续遍历。

代码

class Solution {
private:
    unordered_map<Node*, Node*> created;
public:
    Node* copyRandomList(Node* head) {
        if(head==nullptr) return head;//如果头结点为空，返回其本身
        Node* pre = new Node(0);//假头节点，用于避免边界判断带来的麻烦
        Node* cur = head;//当前指针指向头节点
        while(cur!=nullptr){//依次遍历链表各节点，同时构造新链表
            if(!created.count(cur)){//如果当前指针指向的旧链表节点未被创建（其有可能在之前的节点完善random指针时被创建）
                created[cur] = new Node(cur->val);//则创建之
            }//如果已被创建则直接使用之
            pre -> next = created[cur];//将前一节点的next指针指向本节点
            pre = pre -> next;//更新pre指针指向本节点
            if(cur->random == nullptr) created[cur] -> random = nullptr;//若该节点的random指针指向空，则新链表中的也指向空
            else{//否则完善其random指针指向
                if(!created.count(cur->random)){//如果其random应指向的节点还未创建
                    created[cur->random] = new Node(cur->random->val);//则创建之
                }//并将random指针指向他
                created[cur]->random = created[cur->random];
            }
            cur = cur -> next;//更新当前工作指针指向本节点的下一节点
        }
        return created[head];//返回答案
    }
};

复杂度分析

时间复杂度： O(m)。遍历一次链表的时间消耗
空间复杂度： O(m)。哈希表的空间消耗。

解法四迭代

解题思路

在上述方法中，因为使用了哈希表，所以空间复杂度比较高。这里有另外的一种方法，可以实现O(1)空间复杂度。
具体的，我们首先遍历一遍旧链表，并新建复制节点，注意，这次我们将新建的节点直接链接在原节点的后边，同时保持链表的完整性。例如对于链表A→B→C，我们可以将其拆分为A → A′→ B → B′→ C → C′。对于任意一个原节点S，其拷贝节点S'即为其后继节点。通过这样的方式，我们很容易就能找到新节点的random节点所指向的正确节点，因为他们就是旧链表中原节点中random指针指向节点的后继结点或者空节点，通过一次遍历我们就能完善所有节点的random指针。最后，再通过一次遍历将两个链表断开，即可完成深拷贝操作。
注意，原链表也必须还原，不然无法通过。

代码

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(!head) return head;//如果头结点为空，返回其本身

        //第一次遍历，将拷贝节点链接到原节点之后，使其成为原节点的后继结点
        Node* temp = head;
        while(temp!=nullptr){
            Node* newNode = new Node(temp->val);
            newNode -> next = temp -> next;
            newNode -> random = temp -> random;
            temp -> next = newNode;
            temp = newNode -> next;
        }

        //第二次遍历，完善各拷贝节点的random指向
        temp = head;
        Node* ans = head -> next;
        while(temp!=nullptr){
            if(temp->next->random != nullptr){
                temp->next->random = temp->next->random->next;
            } 
            temp = temp -> next -> next;
        }

        //第三次遍历，将新旧链表断链并恢复原链表
        temp = head;
        while(temp!=nullptr){
            Node* copy = temp -> next -> next;
            if(!copy) break;
            temp -> next -> next = copy -> next;
            temp -> next = copy;
            temp = copy;
        }
        temp -> next = nullptr;
        return ans;
    }
};

复杂度分析

时间复杂度： O(m)。遍历一次链表的时间消耗
空间复杂度： O(1)。只需常数个额外变量。

Tips：

在上面的分析中可以看到，对于设计链表的，包含增删等操作时，使用假头/尾节点可以避免很多边界判断带来的麻烦。这一点可以在解题过程中多加应用。

更多知识内容分享：力扣个人主页https://leetcode-cn.com/profile/articles/
CSDN个人主页https://blog.csdn.net/qq_39255924
牛客个人主页https://blog.nowcoder.net/newcoderthewarrior
alt

【Warrior刷题笔记】剑指offer 6 24 35. 三道题，让你学会链表递归迭代辅助栈

题目一 从尾到头打印链表

1.描述

2.示例

解法一 迭代+辅助栈

解题思路

代码

复杂度分析

解法二 递归

解题思路

代码

复杂度分析

题目二 反转链表

1.描述

2.示例

解法一 迭代+辅助栈

解题思路

代码

复杂度分析

解法二 迭代+三指针

解题思路

代码

复杂度分析

解法三 递归

解题思路

代码

复杂度分析

题目三 复杂链表的深拷贝

1.描述

2.示例

解法一 暴力遍历

解题思路

代码

复杂度分析

解法二 递归+哈希表

解题思路

代码

复杂度分析

解法三 迭代 + 哈希表

解题思路

代码

复杂度分析

解法四 迭代

解题思路

代码

复杂度分析

Tips：

题目一从尾到头打印链表

解法一迭代+辅助栈

解法二递归

题目二反转链表

解法一迭代+辅助栈

解法二迭代+三指针

解法三递归

题目三复杂链表的深拷贝

解法一暴力遍历

解法二递归+哈希表

解法三迭代 + 哈希表

解法四迭代