文章目录
狄利克雷卷积
文中 ∗表示卷积 ⋅ 表示乘积
就是有两个积性函数 g 和 f
g∗f=d∣n∑g(n)⋅f(dn)
这个就叫做狄利克雷卷积
一些常见的积性数论函数
①单位元: e(n)=[n==1]
就是说只有当n等于1的时候等于1,其他时候都等于0,这个中括号也是常见的表达方式,就是说只有当中括号里面的东西为真的时候是1
结论: e=μ∗1
证明看这里:https://blog.csdn.net/swustlpf/article/details/78634667
②常值函数: 1(n)=1
③单位函数: Id(n)=n
结论: Id=φ∗1
证明看这里:https://blog.csdn.net/alan_cty/article/details/50696793#comments
④:欧拉函数: φ(n)
⑤:莫比乌斯函数: μ(n)
杜教筛
假如要求积性函数 f 的前 n 项和
就要找一个积性函数 g 使得 ∑i=1ng∗f 是个很好求得的
也就是说假如 h=g∗f,那么 ∑i=1nh(i)这个是非常好求的,并且假设求出来就等于 AAA
然后就是杜教筛的正文了:
就是对等式的右边进行变换:
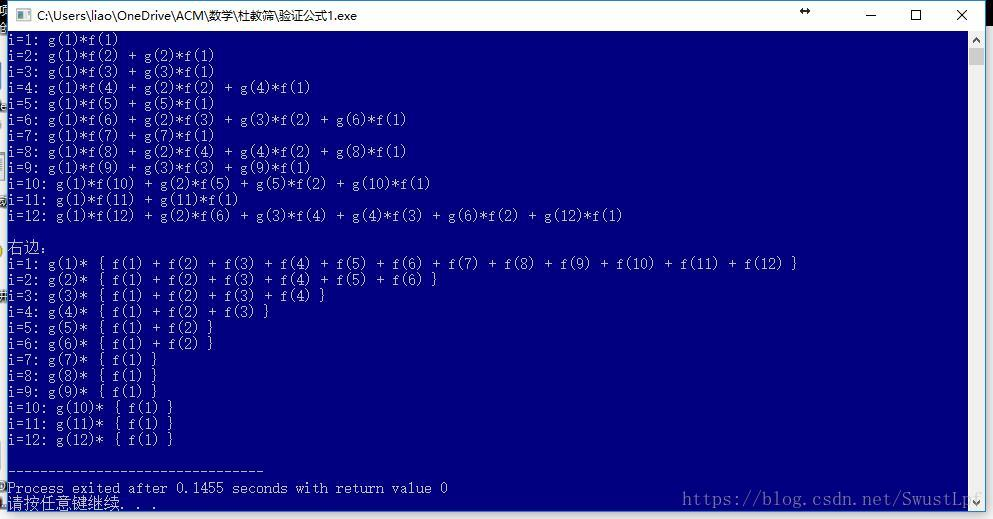
i=1∑nd∣i∑g(d)⋅f(di)=i=1∑ng(i)⋅j=1∑inf(j)
感觉这一步就是最关键的了,我看了好久都不是很懂,然后打了个表来验证
哎呀我懂了数论题中交换求和符号,快夸奖我٩(๑>◡<๑)۶
左边的公式感觉就是把每个数拆成他有的两个因子在那里乘,右边的公式感觉就是收集一下每个因子乘了哪些数
哇我真的是反应不过来这个啊T_T
然后后面的还好看懂,用 S(n) 表示 f 的前 n 项和:
=i=1∑ng(i)⋅S(in)
然后再把 i=1 这一项单独拿出来:
=g(1)⋅S(n)+i=2∑ng(i)⋅S(in)
这样 S(n) 的关系式就有了,只不过前面有个系数 g(1)
再把左边那好算的一坨 ∑i=1ng∗f 写回来,假设他算出来等于 AAA
因此就是:
AAA=g(1)⋅S(n)+i=2∑ng(i)⋅S(in)
所以最终 S(n) 就是:
S(n)=g(1)1⋅(AAA−i=2∑ng(i)⋅S(in))
然后如果 g(i) 是个常数,那么计算 S(in) 的时候要 数论分块 加速一哈
就是说 in 这个值在 [i,n/in] 这段区间内都是一样的
#51nod 1239 欧拉函数前缀和
http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1239
好现在来套公式做题练练手:
首先要找一个合适的 g 函数,来和轻易地求出 AAA
对于欧拉函数,找的是 1 函数 1(n)
不懂怎么找到的,难道是凑的???
因为 φ∗1=id
也就是说 ∑d∣nφ(d)⋅1(dn)=n
也就是那个结论: d∣n∑φ(d)=n
证明阔以看这位童鞋滴,他的第二种比较好理解
那我们的 AAA=∑g∗f=∑i=1n∑d∣iφ(d)=∑i=1ni=2n(n+1)
所以我们这里的 AAA 就是 2n(n+1)
再来化简右边,把 g 函数换成 1 函数:
i=1∑nd∣i∑1(n)⋅φ(di)
=i=1∑n1(i)⋅j=1∑inφ(j)
再把 i=1 这一项单独弄出来
=1(1)⋅S(n)+i=2∑n1(i)⋅S(in)
而 1 函数是常函数一直等于1 ,就简化一下,最终就推出这个公式,左边=右边:
2n(n+1)=S(n)+i=2∑nS(in)
所以最终就是:
S(n)=2n(n+1)−i=2∑nS(in)
而这种就是属于阔以分块加速的~
#include"bits/stdc++.h"
using namespace std;
const int maxn=1e6+5;
const int MOD=1e9+7;
const int inv2=5e8+4;
typedef long long LL;
bool vis[maxn];
LL phi[maxn],Sphi[maxn];//Å·Àº¯Êý£¬Å·Àº¯Êýǰ׺ºÍ
vector<int>prime;
map<LL,LL>Mp;
void PHI(int n)
{
memset(vis,1,sizeof(vis));
phi[1]=1;
Sphi[1]=1;
for(int i=2;i<=n;i++)
{
if(vis[i])
{
prime.push_back(i);
phi[i]=i-1;
}
for(int j=0;j<prime.size()&&i*prime[j]<=n;j++)
{
vis[i*prime[j]]=0;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
Sphi[i]=(Sphi[i-1]+phi[i])%MOD;
}
}
LL S(LL n)
{
if(n<=maxn-5)return Sphi[n];
if(Mp[n])return Mp[n];
LL res=(n%MOD)*((n+1)%MOD)%MOD*inv2%MOD;
for(LL i=2,j;i<=n;i=j+1)
{
j=n/(n/i);
res-=(LL)(j-i+1)%MOD*S(n/i)%MOD;
res%=MOD;
}
res=(res+MOD)%MOD;
return Mp[n]=res;
}
int main()
{
PHI(maxn-5);
LL N;
while(cin>>N)
{
cout<<S(N)<<endl;
}
}
#51nod 1244 莫比乌斯函数前缀和
http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1244
这次选的 g 函数也是 1 函数
使用的性质是: μ∗1=e
证明阔以看这里
也就是 ∑d∣nμ(d)⋅1(dn)=∑d∣nμ(d)=e
这样子计算出的 AAA=∑i=1n∑d∣iμ(d)=1
那直接套公式阔以得到: S(n)=1−i=2∑nS(in)
#51nod 1237 最大公约数之和 V3
http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1237
用 f(d) 表示 gcd(i,j)=d 的个数
那么其实就是求:
d=1∑nd⋅f(d)
而怎么求 f(d) 喃?很经典的一个就是用莫比乌斯反演,但是这样是 O(n) 的
还有一个公式就是 2i=1∑nφ(i)−1
为什么喃?
i=1∑nj=1∑i[gcd(i,j)==1]=φ(i)
相当于枚举 i 然后 j 是小于 i 中与 i 互质的,那么这不就是 φ(i) 的个数么?
然后就是 j>=i 的时候,相当于枚举 j ,因此是两倍,最后减个 1 是因为 (1,1) 这个是计算进了欧拉函数中的,算了两次,所以要减去1
而我们要的是 gcd(i,j)=d 的,这样处理一哈就行了:
i=1∑nj=1∑n[gcd(i,j)==d]=i=1∑dnj=1∑dn[gcd(i,j)==1]=2i=1∑dnφ(i)−1=2S(dn)−1
于是公式就出来了:
ans=d=1∑nd⋅(2S(dn)−1)
这样看起来好像也是 O(n) 的, d 要遍历 1 到 n,但是我们阔以数论分块~~~
在 [d,n/(n/d)] 这一段内的 S(dn) 是相同的,而这一段的 d 也只是个等差数列非常好求,因此,就阔以写了~
#include"bits/stdc++.h"
using namespace std;
const int maxn=1e6+5;
const int MOD=1e9+7;
const int inv2=5e8+4;
typedef long long LL;
bool vis[maxn];
LL phi[maxn],Sphi[maxn];//Å·Àº¯Êý£¬Å·Àº¯Êýǰ׺ºÍ
vector<int>prime;
map<LL,LL>Mp;
void PHI(int n)
{
memset(vis,1,sizeof(vis));
phi[1]=1;
Sphi[1]=1;
for(int i=2;i<=n;i++)
{
if(vis[i])
{
prime.push_back(i);
phi[i]=i-1;
}
for(int j=0;j<prime.size()&&i*prime[j]<=n;j++)
{
vis[i*prime[j]]=0;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
Sphi[i]=(Sphi[i-1]+phi[i])%MOD;
}
}
LL S(LL n)
{
if(n<=maxn-5)return Sphi[n];
if(Mp[n])return Mp[n];
LL res=(n%MOD)*((n+1)%MOD)%MOD*inv2%MOD;
for(LL i=2,j;i<=n;i=j+1)
{
j=n/(n/i);
res-=(LL)(j-i+1)%MOD*S(n/i)%MOD;
res%=MOD;
}
res=(res+MOD)%MOD;
return Mp[n]=res;
}
int main()
{
PHI(maxn-5);
LL N;
while(cin>>N)
{
LL res=0;
for(LL d=1,j;d<=N;d=j+1)
{
j=N/(N/d);
LL t1=(d+j)%MOD;
LL t2=(j-d+1)%MOD;
LL t=t1*t2%MOD*inv2%MOD;
res+=t%MOD*(2LL*S(N/d)-1)%MOD;
res%=MOD;
}
res=(res+MOD)%MOD;
cout<<res<<endl;
}
}
#51nod 1188 最大公约数之和 V2
题目链接:http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1188
还是从最古老的公式入手,就是想求一个数m与n以内的数互质的个数: i=1∑m[gcd(i,m)==1]=d∣m∑μ(d)⋅dn
当 m=n 时,很明显就是欧拉函数的定义,而且也退化成了一个常见的狄利克雷卷积的结论:
φ=μ∗id
这是求的 gcd=1 的方法,要是求的 gcd=d怎么办喃,就是同时除以 d 就转换成了 gcd=1 的了,那么 dn 内互质的个数就是 φ(dn)
然后就是枚举因子 d 的时候只用枚举到 sqrt(n),,因为如果 d 是n的因子,那么 dn 肯定也是 n的因子,这样就不会超时了,这个很关键
因为做V2的时候脑子有点反应不过来,因此在V1这里先做个铺垫,就是求V1,如果数据范围改成1e6的话,就这个阔以改成筛法,感觉线性筛就有点考脑子了。
筛法只能过1e6的数据
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
const int MOD=1e9+7;
LL N,M;
vector<int>prime;
int phi[maxn];
bool vis[maxn];
map<LL,LL>Mp;
LL ans[maxn];
void PHI(int n)
{
memset(vis,1,sizeof(vis));
phi[1]=1;
for(int i=2;i<=n;i++)
{
if(vis[i])
{
prime.push_back(i);
phi[i]=i-1;
}
for(int j=0;j<prime.size()&&i*prime[j]<=n;j++)
{
vis[i*prime[j]]=0;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
int main()
{
PHI(maxn-5);
for(LL d=1;d<=maxn-5;d++)//ö¾ÙÒò×Ó
{
for(LL i=1;d*i<=maxn-5;i++)
{
LL n=d*i;
ans[n]+=d*phi[i];//Ï൱ÓÚÊǶÔn=d*iÕâ¸öÊýµÄ¹±Ï×
}
}
int N;
while(cin>>N)
{
cout<<ans[N]<<endl;
}
}
理解了这个的话V2就好做了




 京公网安备 11010502036488号
京公网安备 11010502036488号