描述
题目描述
给定我们一颗二叉树,让我们返回它后序遍历的结果
样例解释
样例输入:
{1,#,2,3}
然后我们画一下后序遍历的顺序
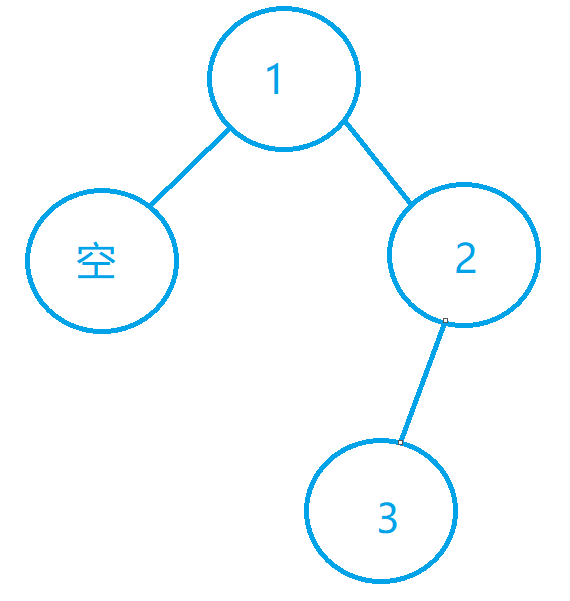
首先这个是我们的二叉树
然后我们开始按照题目要求,先是左子树,再右子树,最后根节点
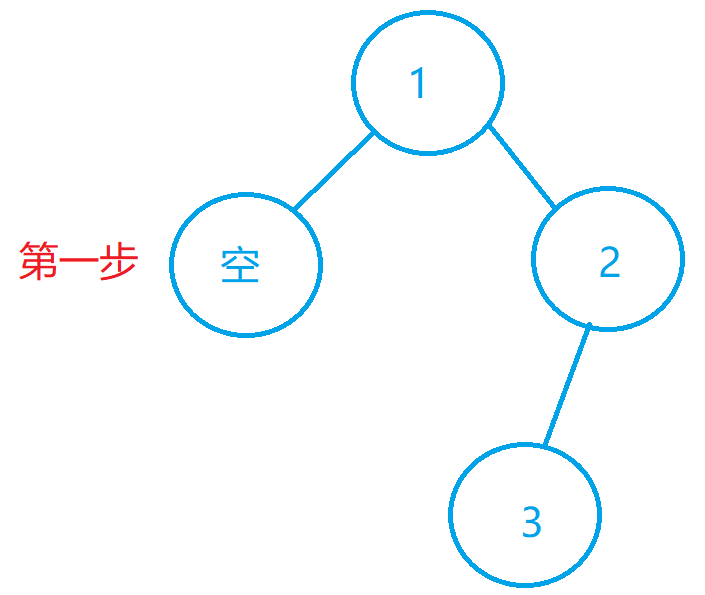
因为这个是空节点直接返回了
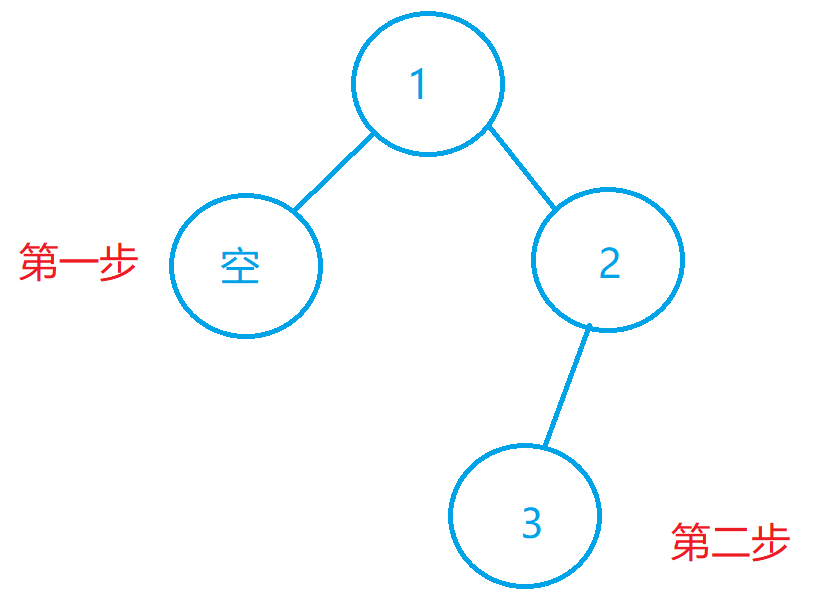
然后我们遍历右子树,一直到了最下面
然后我们往回
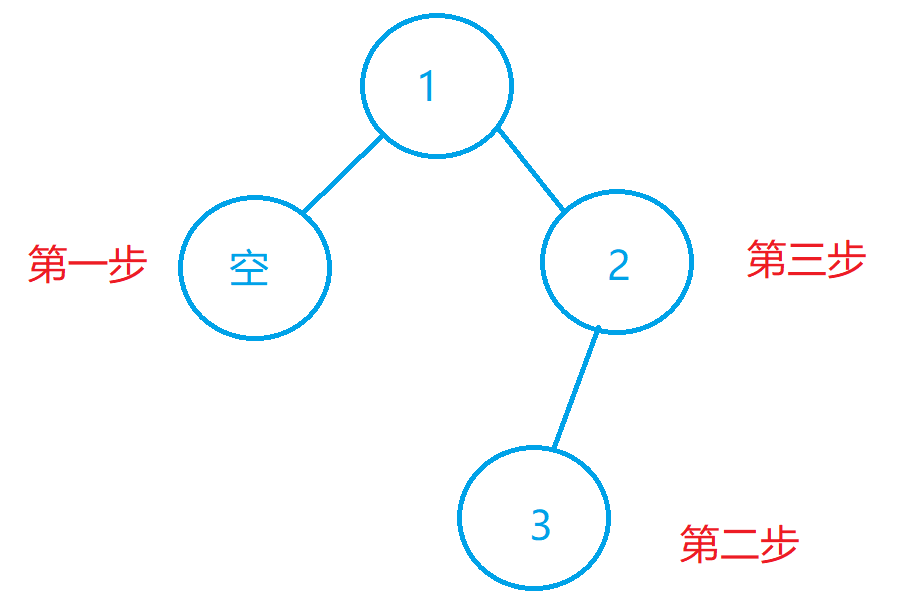
然后我们最后访问根节点
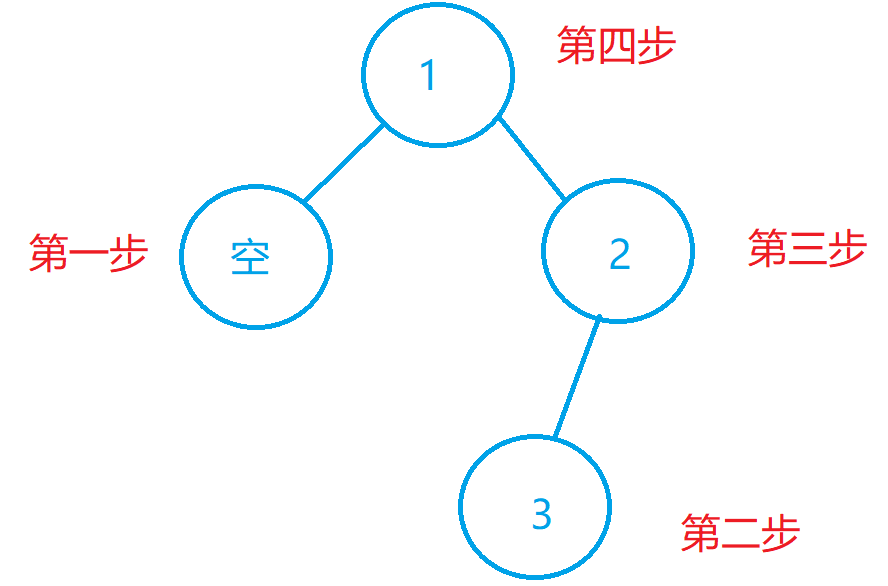
所以最后的样例输出是
[3,2,1]
题解
解法一:递归
解题思路
我们按照题目描述的,先遍历左子树,然后右子树,最后是根节点,这样的顺序遍历整棵树,遇到空节点返回,左右都遍历完了之后再存入值
代码实现
class Solution {
vector<int> res;
public:
void dfs(TreeNode* root) {
if (root == nullptr) return;
// 空节点返回
dfs(root->left);
// 左子树
dfs(root->right);
// 右子树
res.push_back(root->val);
// 存值
}
vector<int> postorderTraversal(TreeNode* root) {
dfs(root);
// 遍历树
return res;
}
};
时空复杂度分析
时间复杂度:
理由如下:我们遍历了二叉树的所有节点,节点数为
空间复杂度: 平均,最坏
理由如下:空间与我们的栈的深度有关系,一般是树的高度,但是极限情况下,成为一条链,那么就是
解法二:迭代法
解题思路
其实递归就是系统给我们分配一个栈,这里我们可以自己使用STL库里的栈来实现我们的这个操作,本质上就是先遍历左子树,一直到了最后全部入栈,然后取出栈顶元素,就是我们左子树最下面的元素,然后往后弹出,分叉路口的时候重复压栈
代码实现
class Solution {
vector<int> res;
stack<TreeNode*> st;
public:
vector<int> postorderTraversal(TreeNode* root) {
if (root == nullptr) return res;
TreeNode* pre = nullptr;
// 设置一个前驱接节点
while (root != nullptr || st.size()) {
while (root != nullptr) st.push(root), root = root->left;
// 如果没有到左子树最底下的点,继续入栈
root = st.top(), st.pop();
// 取出最后一个元素,就是我们的后序遍历的第一个元素
if (root->right and root->right != pre) {
st.push(root), root = root->right;
// 我们这个点不空,然后且不是上一个节点,我们继续入栈
} else {
res.push_back(root->val), pre = root, root = nullptr;
}
}
return res;
}
};
时空复杂度分析
时间复杂度:
理由如下:我们遍历了二叉树的所有节点,节点数为
空间复杂度: 平均,最坏
理由如下:空间与我们的栈的深度有关系,一般是树的高度,但是极限情况下,成为一条链,那么就是






 京公网安备 11010502036488号
京公网安备 11010502036488号