利用特征向量的属性,矩阵 A 可以变成一个对角化矩阵 Λ。
1. 对角化
假设一个 n×n 的矩阵 A 有 n 个线性不相关的特征向量 x1,⋯,xn ,把它们作为特征向量矩阵 S 的列,那么就有 S−1AS=Λ。
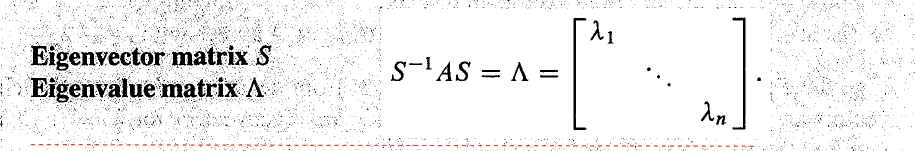
矩阵 A 被对角化了,因为所有的特征向量位于矩阵 Λ的对角线上。
证明过程也很简单,首先我们计算 AS。
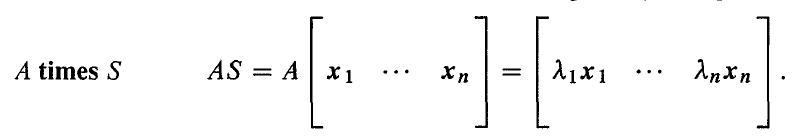
一个技巧就是将 AS 分解成 SΛ。

所以我们有
AS=SΛS−1AS=ΛA=SΛS−1
矩阵 S 有逆矩阵,因为我们假设它的列是 n 个线性不相关的特征向量。如果没有 n 个线性不相关的特征向量,我们就不能进行对角化。
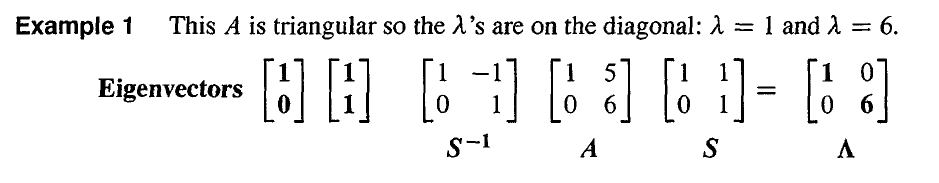
由 A=SΛS−1 可得, A2=SΛS−1SΛS−1=SΛ2S−1,平方后我们得到** S 中相同的特征向量和 Λ 中平方的特征值**。同理,我们可以得到 k 次方为 Ak=SΛkS−1。
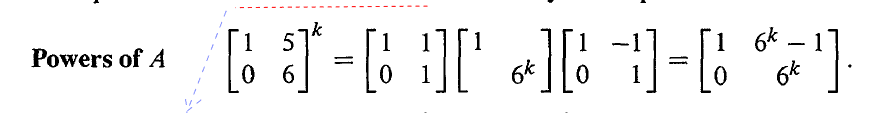
当 k=1 时,我们得到 A.当 k=0 时,我们得到 A0=I。当 k=−1 时,我们得到 A−1。
再继续往下进行之前,有几点需要我们注意。
- 如果特征值 λ1,⋯,λn 全部都不相同,那么自动地特征向量 x1,⋯,xn 就是线性不相关的。任意没有重复特征值的矩阵都可以被对角化。
证明:
假设 c1x1+⋯+cnxn=0,我们乘以矩阵 A,有
c1λ1x1+⋯+cnλnxn=0(1)
然后,乘以 λn 并减去上面的式子 (1),有
c1λnx1+⋯+cnλnxn=0(2)
c1(λn−λ1)x1+⋯+cn−1(λn−λ1)xn−1=0(3)
这会消去 xn,我们继续用 (3) 式分别乘以 A 和 λn−1,再相减, xn−1 就也被消去了。一直重复这个过程,最后,我们就只剩下了 x1。
c1(λn−λ1)(λn−1−λ1)⋯(λ2−λ1)x1=0(4)
因为特征值互不相同,因此有 c1=0,同理我们可得所有的系数都为 0,也即零空间只有零向量,所以这些特征向量是线性不相关的。
在上面的例子中,如果我们互换特征向量的顺序,那么 Λ 中特征值的顺序也要相应改变。
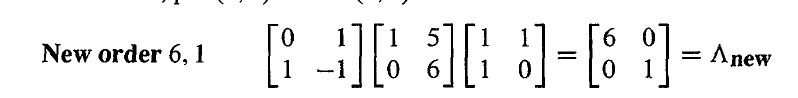
- 一些矩阵没有足够的特征向量,因此不能被对角化,特别是注意有重复特征值的情况。

而且要注意,可逆性和可对角化性之间没有联系。可逆性和是否存在零特征值有关,而可对角化性和是否有足够的特征向量有关。
2. 斐波那契数列
斐波那契序列满足 Fk+2=Fk+1+Fk。为了找到 F100,我们可以从 F2 开始,每次求出一个新的值,直至得到 F100。线性代数则给出了一个更好的方法,我们将之转化为 uk+1=Auk 的问题。
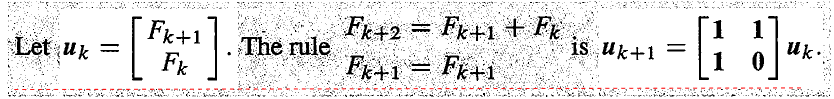
每一次我们都乘以矩阵 A,100 次后我们就得到了 u100=A100u0。
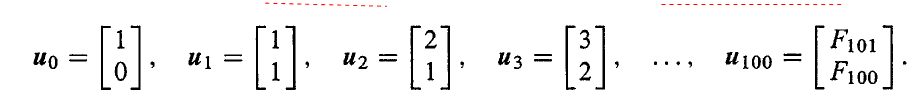
这样,我们就可以利用特征值来求解了。

求解特征方程,我们可以得到两个特征值分别为:

进而得到两个特征向量分别为:
x1=[λ11]x2=[λ21]
然后我们将 u0 表示为特征向量的线性组合。

那么就有
u100=A100u0=λ1−λ21A100(x1−x2)=λ1−λ2λ1100x1−λ2100x2
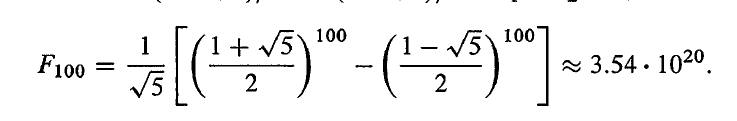
上式中的第二项底数小于 0.5,因此会渐渐趋向于 0,也就是说随着 n 增大逐渐只有第一项有效。
F100F101≈21+5 ≈1.618
这个数字就是我们众所周知的黄金比例。
3. A 的幂
斐波那契数列是一个典型的差分方程,每一步我们都乘以矩阵 A。下面我们来看一下对角化是怎么来快速计算 Ak 的。
Aku0=(SΛS−1)⋯(SΛS−1)u0=SΛkS−1u0
然后我们将 u0 表示为特征向量的线性组合
-
u0=c1x1+⋯+cnxn→u0=Sc→c=S−1u0
-
Au0=c1Ax1+⋯+cnAxn=c1λ1x1+⋯+cnλnxn
-
Aku0=c1λ1kx1+⋯+cnλnkxn=SΛkc

4. 不可对角化矩阵
特征值 λ 可能会有重复情况,这时候我们想知道它的重复度(multiplicity),有两种方法来计量。
- 几何重数(Geometric Multiplicity)与特征值 λ 对应的线性不相关的特征向量的个数
- 代数重数(Algebraic Multiplicity)特征值 λ 的重复次数,也就是 det(A−λI) 的重根数
几何重数小于等于代数重数。
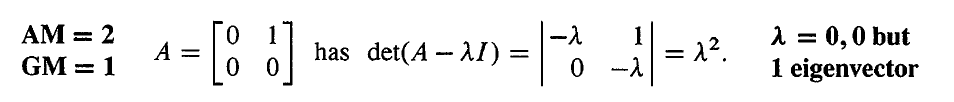
几何重数小于代数重数说明特征向量数量不够,也就是说 A 不能被对角化。
5. AB 和 A+B 的特征值
让我们来猜一猜 AB 的特征值是多少?
你可能会说是它们各自特征值的积。
ABx=Aβx=βAx=βλx
但是,通常情况下 A 和 B 的特征向量是不相同的,因此上面的证明是错误的。同样,两个矩阵各自特征值的和也通常不是两个矩阵和的特征值。
但是,如果 x 同时是 A 和 B 的特征向量。那么有
ABx=λβx=BAx→AB=BA
因此,如果 A 和 B 都可以被对角化,它们拥有相同的特征向量当且仅当 AB=BA。
获取更多精彩,请关注「seniusen」!





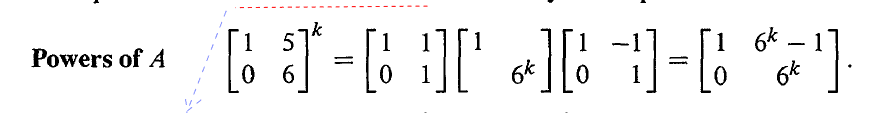
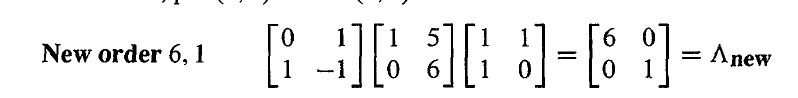

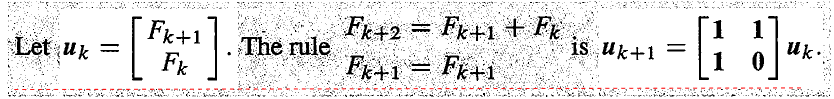
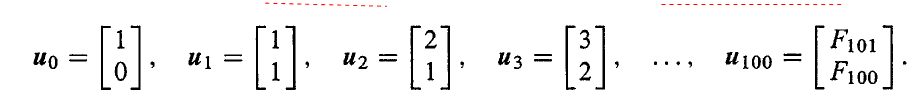



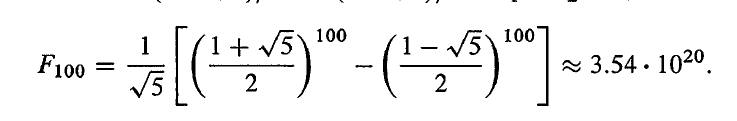

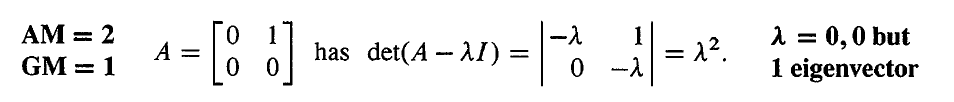


 京公网安备 11010502036488号
京公网安备 11010502036488号