FFT
FFT
FFT的全称是 Fast Fourier Transform 即快速傅里叶变换
傅里叶变换是复变函数的重要内容,傅里叶变换分为离散和连续傅里叶变换
傅里叶变换实现从时域到频域的转换,是信号与系统重要的分析工具
连续傅里叶变换
![此处输入图片的描述][1]
离散傅里叶变换(DFT discrete Fourier transform)
将离散的序列值进行频域到时域的转换,就叫做离散傅里叶变换
如果有
x(n)={xN(n)00<=n<=N−1n为其余值
离散傅里叶变换DFT
X(k)=DFT[x(n)]=n=0∑n=N−1x(n)∗WNkn(WN=e−j2π/N)
即是 $ X(k)= x_0 + x_1(W_Nk)1 + x_2(W_Nk)2+…+ x_{N-1}(W_Nk){N-1}$
离散傅里叶逆变换IDFT
x(n)=IDFT[X(k)]=N1n=0∑k=N−1X(k)∗WN−kn
DFT 矩阵形式
FFT
FFT 不是一种新的变换,只是DFT的快速实现的一种方法!!
FFT 要求 N=2k,所以不足2的幂次数的要补零
####已知
- WN2∗k=e−Nj2π∗2k=e−N/2j2π∗k=WN/2k(1)
- WNk+N/2=e−Nj2π∗(k+N/2)=−e−Nj2π∗(k)(2)
FFT 具体方法
X(k)=x0+x1(WNk)1+x2(WNk)2+...+xN−1(WNk)N−1
进行奇偶分离
X(k)=x0+x2(WNk)2+...xN−2(WNk)N−2+x1(WNk)1+x3(WNk)3+...+xN−1(WNk)N−1
=x0+x2(WN/2k)1+...+xN−2∗(WN/2k)N/2−1
+Wk(x1+x3∗(WN/2k)+1xN−1∗(WN/2k)N/2−1)
令 A0(x)=x0+x2(x)1+...+xN−2∗(x)N/2−1
A1(x)=x1+x3∗(x)+1xN−1∗(x)N/2−1
X(k)=A0(WN/2k)+WkA1(WN/2k)(3)
同理得 X(k+N/2)=A0(WN/2k)−WkA1(WN/2k)(4)
于是现在从求 X(0),X(1),...,X(N−1)
变成了求 A0(0),A0(1),...,A0(N/2−1)
和 A1(0),A1(1),...,A1(N/2−1)
这样利用分治的思想,复杂度是 nlog(n)
递归实现比较麻烦,而且需要额外申请空间,就不再详细介绍了,所以一般采用bit反转来实现
递归分组的时候
x(0)x(1)x(2)x(3)x(4)x(5)x(6)x(7)
x(0)x(2)x(4)x(6)∣x(1)x(3)x(5)x(7)
x(0)x(4)∣x(2)x(6)∣x(1)x(5)∣x(3)x(7)
发现规律
FFT算法步骤
- bit反转
- 分治
- 合并
IDFT 的时候只需要把$W $换成 W−1 就ok了
下面是模板
模板
// 刘汝佳的板子 调用的时候直接 v1*v2 就行了, v1 和 v2 的类型是vector<double>
// 也可以自己修改
#include <bits/stdc++.h>
#define mem(ar,num) memset(ar,num,sizeof(ar))
#define me(ar) memset(ar,0,sizeof(ar))
#define lowbit(x) (x&(-x))
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int prime = 999983;
const int INF = 0x7FFFFFFF;
const LL INFF =0x7FFFFFFFFFFFFFFF;
//const double pi = acos(-1.0);
const double inf = 1e18;
const double eps = 1e-6;
const LL mod = 1e9 + 7;
int dr[2][4] = {1,-1,0,0,0,0,-1,1};
// UVa12298 Super Poker II
// Rujia Liu
const long double PI = acos(0.0) * 2.0;
typedef complex<double> CD;
// Cooley-Tukey的FFT算法,迭代实现。inverse = false时计算逆FFT
inline void FFT(vector<CD> &a, bool inverse) {
int n = a.size();
// 原地快速bit reversal
for(int i = 0, j = 0; i < n; i++) {
if(j > i) swap(a[i], a[j]);
int k = n;
while(j & (k >>= 1)) j &= ~k;
j |= k;
}
double pi = inverse ? -PI : PI;
for(int step = 1; step < n; step <<= 1) {
// 把每相邻两个“step点DFT”通过一系列蝴蝶操作合并为一个“2*step点DFT”
double alpha = pi / step;
// 为求高效,我们并不是依次执行各个完整的DFT合并,而是枚举下标k
// 对于一个下标k,执行所有DFT合并中该下标对应的蝴蝶操作,即通过E[k]和O[k]计算X[k]
// 蝴蝶操作参考:http://en.wikipedia.org/wiki/Butterfly_diagram
for(int k = 0; k < step; k++) {
// 计算omega^k. 这个方法效率低,但如果用每次乘omega的方法递推会有精度问题。
// 有更快更精确的递推方法,为了清晰起见这里略去
CD omegak = exp(CD(0, alpha*k));
for(int Ek = k; Ek < n; Ek += step << 1) { // Ek是某次DFT合并中E[k]在原始序列中的下标
int Ok = Ek + step; // Ok是该DFT合并中O[k]在原始序列中的下标
CD t = omegak * a[Ok]; // 蝴蝶操作:x1 * omega^k
a[Ok] = a[Ek] - t; // 蝴蝶操作:y1 = x0 - t
a[Ek] += t; // 蝴蝶操作:y0 = x0 + t
}
}
}
if(inverse)
for(int i = 0; i < n; i++) a[i] /= n;
}
// 用FFT实现的快速多项式乘法
inline vector<double> operator * (const vector<double>& v1, const vector<double>& v2) {
int s1 = v1.size(), s2 = v2.size(), S = 2;
while(S < s1 + s2) S <<= 1;
vector<CD> a(S,0), b(S,0); // 把FFT的输入长度补成2的幂,不小于v1和v2的长度之和
for(int i = 0; i < s1; i++) a[i] = v1[i];
FFT(a, false);
for(int i = 0; i < s2; i++) b[i] = v2[i];
FFT(b, false);
for(int i = 0; i < S; i++) a[i] *= b[i];
FFT(a, true);
vector<double> res(s1 + s2 - 1);
for(int i = 0; i < s1 + s2 - 1; i++) res[i] = a[i].real(); // 虚部均为0
return res;
}
//kuangbin 的板子,需要一些处理才能用
// 1 首先补成2^n 的形式,然后传入复数
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
using namespace std;
const double PI = acos(-1.0);
struct complex
{
double r,i;
complex(double _r = 0,double _i = 0)
{
r = _r; i = _i;
}
complex operator +(const complex &b)
{
return complex(r+b.r,i+b.i);
}
complex operator -(const complex &b)
{
return complex(r-b.r,i-b.i);
}
complex operator *(const complex &b)
{
return complex(r*b.r-i*b.i,r*b.i+i*b.r);
}
};
void change(complex y[],int len)
{
int i,j,k;
for(i = 1, j = len/2;i < len-1;i++)
{
if(i < j)swap(y[i],y[j]);
k = len/2;
while( j >= k)
{
j -= k;
k /= 2;
}
if(j < k)j += k;
}
}
void fft(complex y[],int len,int on)
{
change(y,len);
for(int h = 2;h <= len;h <<= 1)
{
complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
for(int j = 0;j < len;j += h)
{
complex w(1,0);
for(int k = j;k < j+h/2;k++)
{
complex u = y[k];
complex t = w*y[k+h/2];
y[k] = u+t;
y[k+h/2] = u-t;
w = w*wn;
}
}
}
if(on == -1)
for(int i = 0;i < len;i++)
y[i].r /= len;
}
const int MAXN = 400040;
complex x1[MAXN];
int a[MAXN/4];
long long num[MAXN];//100000*100000会超int
long long sum[MAXN];
int main()
{
int T;
int n;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
memset(num,0,sizeof(num));
for(int i = 0;i < n;i++)
{
scanf("%d",&a[i]);
num[a[i]]++;
}
sort(a,a+n);
int len1 = a[n-1]+1;
int len = 1;
while( len < 2*len1 )len <<= 1;
for(int i = 0;i < len1;i++)
x1[i] = complex(num[i],0);
for(int i = len1;i < len;i++)
x1[i] = complex(0,0);
fft(x1,len,1);
for(int i = 0;i < len;i++)
x1[i] = x1[i]*x1[i];
fft(x1,len,-1);
for(int i = 0;i < len;i++)
num[i] = (long long)(x1[i].r+0.5);
len = 2*a[n-1];
//减掉取两个相同的组合
for(int i = 0;i < n;i++)
num[a[i]+a[i]]--;
//选择的无序,除以2
for(int i = 1;i <= len;i++)
{
num[i]/=2;
}
sum[0] = 0;
for(int i = 1;i <= len;i++)
sum[i] = sum[i-1]+num[i];
long long cnt = 0;
for(int i = 0;i < n;i++)
{
cnt += sum[len]-sum[a[i]];
//减掉一个取大,一个取小的
cnt -= (long long)(n-1-i)*i;
//减掉一个取本身,另外一个取其它
cnt -= (n-1);
//减掉大于它的取两个的组合
cnt -= (long long)(n-1-i)*(n-i-2)/2;
}
//总数
long long tot = (long long)n*(n-1)*(n-2)/6;
printf("%.7lf\n",(double)cnt/tot);
}
return 0;
}
[1]: https://ss1.baidu.com/6ONXsjip0QIZ8tyhnq/it/u=3356269930,1126074676&fm=58
[2]: https://img-blog.csdn.net/20171205133619162?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYTQ5MzgyMzg4Mg==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center
[3]: https://upload-images.jianshu.io/upload_images/9187198-4be4915dd66462ab.jpg?imageMogr2/auto-orient/strip%7CimageView2/2/w/204
#### FFT 题目总结
1. [模板题](http://uoj.ac/problem/34)
2 [Emma and sum of products](https://www.hackerrank.com/challenges/emma-and-sum-of-products/problem)(简单模板题)
3 [Another Fibonacci ](https://www.codechef.com/problems/MOREFB#)(建议配合题解食用较好)
4 [D. Fuzzy Search](http://codeforces.com/problemset/problem/528/D)
5. [ Rock Paper Scissors Lizard Spock.](https://nanti.jisuanke.com/t/26219)(FFT与字符串匹配模板题)
6. [D - Rock Paper Scissors ](https://vjudge.net/contest/229017#problem/D)(FFT 与字符串)



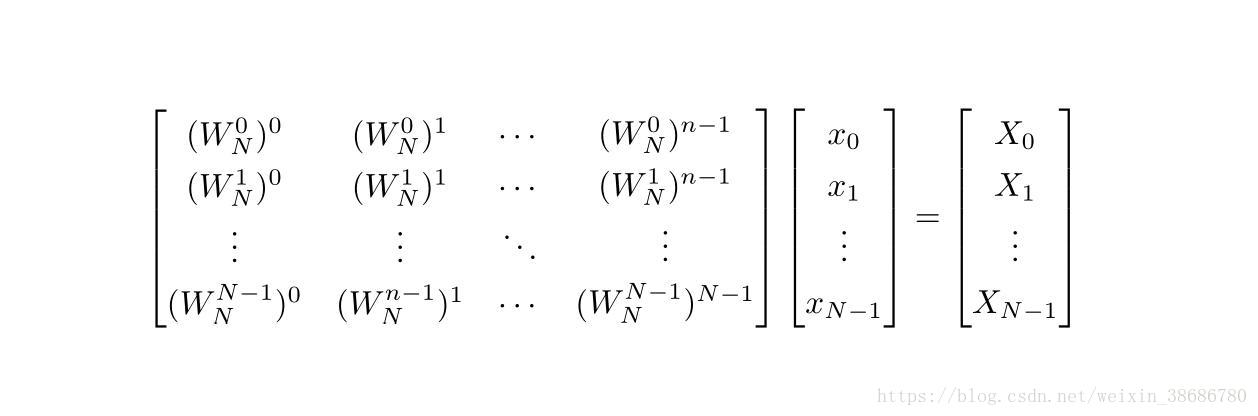


 京公网安备 11010502036488号
京公网安备 11010502036488号