P1790 - [NewOJ Contest 10] 造电梯 - New Online Judge (ecustacm.cn)

题目描述

现在给你一张建筑的平面图，按照要求，建筑的每一个部分都应该是轮椅使用者可以到达的，这意味着必须安装电梯。
给定的平面图是一个n*m的矩阵，里面的数字表示这个位置的高度。可以在建筑中的任意位置放置电梯，电梯可以停在所有楼层。
需要保证可以使用电梯到达所有高楼层。相同高度的楼层之间是互通的，联通准则是四联通。
需要求解最少需要多少个电梯，注意高度为1的不需要电梯。
下图展示了样例2的可视化三维图。
 


 

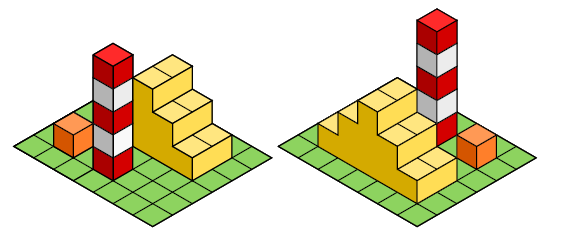
输入格式

输入第一行为n和m(1≤n,m≤500)。
接下来n行，每行m个整数xij，表示平面图，0≤xij≤10^9。

输出格式

输出最少电梯数量

输入样例 

样例1：
2 3
1 2 3
1 3 2

样例2：
6 7
0 0 0 0 0 0 0
0 1 2 3 2 1 0
0 1 2 3 2 1 0
0 0 0 0 0 0 0
0 1 0 5 0 0 0
0 0 0 0 0 0 0

输出样例 

样例1：
2

样例2：
2

 本题的特点在于四联通，所以高楼层的电梯可以将相邻的楼层进行一个包含。可以使用洪水填充的做法。使用一个优先队列来保持每次取出的都是当前最高的楼层，然后对该楼层进行一个遍历，将所有可以包含进来的楼层进行记录。重复这个过程就可以求出答案。

AC代码：

//使用洪水填充法，按照题目中的条件可以看出，在相邻的楼之间可以相互淹没，
// 所以从高向下遍历（使用优先队列），然后使用DFS或BFS的方式
//将下面的楼层覆盖填满。
#include <bits/stdc++.h>

#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;

struct priority_floor{
	int x;
	int y;
	int high;
};
//方法2
struct tmp2 //重写仿函数
{
    bool operator() (struct priority_floor p1, struct priority_floor p2) 
    {
        return p1.high<p2.high; //大顶堆
    }
};

priority_queue<priority_floor, vector<priority_floor>, tmp2> fl;
int node[502][502];
bool is_flood[502][502];
int n, m, cnt = 0;

//搞一个上下左右中的二维数组 
int mv[4][2] = {
  {1,0},{-1,0},{0,-1},{0,1}};

void BFS(int x, int y) {
	is_flood[x][y] = true;
	int nx, ny;
	for (int i=0;i<4;i++) {
		nx = x+mv[i][0];
		ny = y+mv[i][1];
		//碰到边缘不管 
		if (ny>=m||ny<0||nx>=n||nx<0) continue;
		//楼层较低不管 
		if (node[nx][ny]>node[x][y]) continue;
		//高度为0或1的不管 
		if (node[nx][ny]==0||node[nx][ny]==1) continue;
		//覆盖过的不管
		if (is_flood[nx][ny]) continue;
		//剩下的可以接着BFS
		BFS(nx, ny); 
	}
}

int main() {
	IOS;
	cin>>n>>m;
	for (int i=0;i<n;i++) {
		for (int j=0;j<m;j++) {
			cin>>node[i][j];
			if (node[i][j]==0||node[i][j]==1) {
				is_flood[i][j] = true;
			}
			priority_floor p;
			p.x = i;
			p.y = j;
			p.high = node[i][j];
			fl.push(p);
		}
	}
	while (!fl.empty()) {
		priority_floor p = fl.top();
		fl.pop();
//		cout<<p.high<<endl;
		int x = p.x;
		int y = p.y;
		if (is_flood[x][y]) continue;
		BFS(x, y);
		cnt++;
	}
	cout<<cnt;
	return 0;
}