今日小结：今天复习了二分图，差分约束，树状数组，树链剖分和线段树，二分图和差分约束就只下午听了\(lwl\)和\(axm\)讲课，然后因为要准备将树链剖分，所以就先把重点放在了这上面，树链剖分要用到线段树和树状数组的有关知识，所以今天主要就加强了一下这两个方面。

一. 今日完成的题目：

洛谷P3582，洛谷P1558，洛谷P2068，洛谷P2184，洛谷P2846，洛谷P2574

二.

1. 当天完成题目数：6道。

2. 未完成6个题目的原因：

3. 复习的知识点：线段树，差分约束，树链剖分，二分图，树状数组

4.不会题目：洛谷P3979

三：

1. 洛谷P3582 [POI2015]KIN

题目描述

共有\(m\)部电影，编号为\(1——m\)，第\(i\)部电影的好看值为\(w[i]\)。在\(n\)天之中（从\(1~n\)编号）每天会放映一部电影，第\(i\)天放映的是第\(f[i]\)部。你可以选择\(l,r(1 \leq l \leq r \leq n)\)，并观看第\(l,l+1,…,r\)天内所有的电影。如果同一部电影你观看多于一次，你会感到无聊，于是无法获得这部电影的好看值。所以你希望最大化观看且仅观看过一次的电影的好看值的总和。

输入输出格式

输入格式：

第一行两个整数\(n,m(1 \leq m \leq n \leq 1000000)\)。第二行包含\(n\)个整数\(f[1],f[2],…,f[n]\)。第三行包含\(m\)个整数\(w[1],w[2],…,w[m]\)。

输出格式：

输出观看且仅观看过一次的电影的好看值的总和的最大值。

输入输出样例

输入样例#1：

9 4
2 3 1 1 4 1 2 4 1
5 3 6 6

输出样例#1：

15

思路：这道题目我们可以考虑先记录每种电影上一次开播时间和下一次开播时间(即以下代码中的\(last\)数组和\(nxt\)数组)，然后对于每种电影，我们可以先处理中它是否播放过对后面区间的影响情况，然后再对\(n\)个时间点分别考虑，我们可以枚举左端点，然后根据左端点电影的播放情况就可以确定它可以影响到的最右端点，然后不断更新，更新过程中记录最大值，最后那个最大值即为答案。

洛谷P3582(自己写的题解)

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#define ll long long
#define maxn 1000007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int n,m,f[maxn],nxt[maxn],last[maxn],a[maxn];
ll ans;
inline int qread() {            //快读，不解释……
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct Tree {
  ll maxx,lazy;
}tree[maxn<<2];
inline void pushdown(int rt) {    //下放lazy标记。
  if(tree[rt].lazy) {
    tree[ls].lazy+=tree[rt].lazy;
    tree[rs].lazy+=tree[rt].lazy;
    tree[rs].maxx+=tree[rt].lazy;
    tree[ls].maxx+=tree[rt].lazy;
    tree[rt].lazy=0;
  }
}
void modify(int rt,int l,int r,int L,int R,int val) { //区间修改，用于后面的更新。
  if(L>r||R<l) return;
  if(L<=l&&r<=R) {
    tree[rt].lazy+=val;
    tree[rt].maxx+=val;
    return;
  }
  pushdown(rt);
  int mid=(l+r)>>1;
  modify(ls,l,mid,L,R,val),modify(rs,mid+1,r,L,R,val);
  tree[rt].maxx=max(tree[ls].maxx,tree[rs].maxx);
}
int main() {
  n=qread(),m=qread();
  for(int i=1;i<=n;++i) f[i]=qread();
  for(int i=1;i<=m;++i) a[i]=qread();
  for(int i=n;i>=1;--i) nxt[i]=last[f[i]],last[f[i]]=i; //处理出nxt和last数组。
  for(int i=1;i<=m;++i) {
    if(last[i]) {                   //如果这个电影已经播放过。
      int zrj=nxt[last[i]];
      if(zrj) modify(1,1,n,last[i],zrj-1,a[i]);  
      //如果这不是最后一次播放这个电影，那么可以影响到的最右端点是nxt[last[i]]-1，然后last[i]就是左端点，也是第一次看，所以在这个区间加上这个电影的价值。
      else modify(1,1,n,last[i],n,a[i]);  //如果是最后一次，那么它将一直影响到最后。
    }
  }
  for(int i=1;i<=n;++i) {
    ans=max(ans,tree[1].maxx);         //每次更新一下最大值。
    int zrj=nxt[i];
    if(zrj) {                   //如果第二次播放。
      modify(1,1,n,i,zrj-1,-a[f[i]]);  //在这次和之后的一次的区间上价值减去这个电影的价值，因为相同电影看了价值为0。
      if(nxt[zrj]) modify(1,1,n,zrj,nxt[zrj]-1,a[f[i]]); //第二次和第三次之间加上这个电影的价值(因为是以第二次为左端点，只看了一次)。
      else modify(1,1,n,zrj,n,a[f[i]]); //不然就把第二次之后的加上这个价值。
    }
    else modify(1,1,n,i,n,-a[f[i]]);  //没有第二次播放，就从当前时间开始一直到最后，减去这个价值。
  }
  printf("%lld\n",ans);
  return 0;
}

2. 洛谷P1558 色板游戏

题目背景

阿宝上学了，今天老师拿来了一块很长的涂色板。

题目描述

色板长度为\(L\)，\(L\)是一个正整数，所以我们可以均匀地将它划分成\(L\)块\(1\)厘米长的小方格。并从左到右标记为\(1, 2, ... L\)。

现在色板上只有一个颜色，老师告诉阿宝在色板上只能做两件事：

1. "\(C\) \(A\) \(B\) \(C\)" 指在\(A\)到 \(B\) 号方格中涂上颜色 \(C\)。
2. "\(P\) \(A\) \(B\)"指老师的提问：\(A\)到 \(B\)号方格中有几种颜色。

学校的颜料盒中一共有 \(T\) 种颜料。为简便起见，我们把他们标记为 \(1, 2, ... T\). 开始时色板上原有的颜色就为\(1\)号色。 面对如此复杂的问题，阿宝向你求助，你能帮助他吗？

输入输出格式

输入格式：

第一行有\(3\)个整数 \(L (1 \leq L \leq 100000)\), \(T (1 \leq T \leq 30)\) 和 \(O (1 \leq O \leq 100000)\)。 在这里\(O\)表示事件数。
接下来 \(O\) 行, 每行以 "\(C\) \(A\) \(B\) \(C\)" 或 "\(P\) \(A\) \(B\)" 得形式表示所要做的事情(这里 \(A\), \(B\), \(C\) 为整数, 可能\(A\)> \(B\)，这样的话需要你交换\(A\)和\(B\))

输出格式：

对于老师的提问，做出相应的回答。每行一个整数。

输入输出样例

输入样例#1：

2 2 4
C 1 1 2
P 1 2
C 2 2 2
P 1 2

输出样例#1：

2
1

思路：正解貌似是基于二进制来建线段树，但是我不会……于是我就非常暴力的建了\(t\)棵线段树，因为\(t\)只有\(30\)嘛，所以建\(30\)棵线段树也不会爆，没棵线段树代表一个颜色，然后对于每一个\(C\)操作，就是修改要修改的那个颜色的对应线段树的对应修改区间为\(1\)，其余线段树的对应修改区间修改为\(0\)，然后查询就是把每棵线段树的区间颜色数加起来。但是代码可能因为常数优化的不太好等原因，不开\(O(2)\)会\(TLE\)一个点。

代码：

#include<cstdio>
#include<algorithm>
#define maxn 100007
#define ls rt<<1
#define rs rt<<1|1
#define re register
using namespace std;
int n,t,m,sum[31][maxn<<2],lazy[31][maxn<<2];
char s[2];
inline void pushup(int i, int rt) {
  sum[i][rt]=sum[i][ls]+sum[i][rs];
}
inline void pushdown(int i, int rt) {
  if(lazy[i][rt]==-1) {
    sum[i][ls]=sum[i][rs]=0;
    lazy[i][ls]=lazy[i][rs]=-1; 
  }
  else {
    lazy[i][ls]=lazy[i][rs]=lazy[i][rt];
    sum[i][ls]=sum[i][rs]=lazy[i][rt];
  }
  lazy[i][rt]=0;
}
void build(int rt, int l, int r) {
  if(l==r) {
    sum[1][rt]=1;
    return;
  }
  int mid=(l+r)>>1;
  build(ls,l,mid);
  build(rs,mid+1,r);
  pushup(1,rt);
}
void modify(int i, int rt, int l, int r, int L, int R, int val) {
  if(L>r||R<l) return;
  if(L<=l&&r<=R) {
    sum[i][rt]=val;
    if(!val) lazy[i][rt]=-1;
    else lazy[i][rt]=val;
    return;
  }
  if(lazy[i][rt]) pushdown(i,rt);
  int mid=(l+r)>>1;
  if(L<=mid) modify(i,ls,l,mid,L,R,val);
  if(R>mid) modify(i,rs,mid+1,r,L,R,val);
  pushup(i,rt);
}
int csum(int i, int rt, int l, int r, int L, int R) {
  if(L>r||R<l) return 0;
  if(L<=l&&r<=R) return sum[i][rt];
  if(lazy[i][rt]) pushdown(i,rt);
  int mid=(l+r)>>1;
  return csum(i,ls,l,mid,L,R)+csum(i,rs,mid+1,r,L,R);
}
int main() {
  scanf("%d%d%d",&n,&t,&m);
  build(1,1,n);
  for(re int i=1,l,r,v;i<=m;++i) {
    scanf("%s%d%d",s,&l,&r);
    if(l>r) swap(l,r);
    if(s[0]=='C') {
      scanf("%d",&v);
      for(re int k=1;k<=t;++k) {
        if(k!=v) modify(k,1,1,n,l,r,0);
        else modify(k,1,1,n,l,r,1);
      }
    }
    else {
      int zrj=0;
      for(re int k=1;k<=t;++k) 
        if(csum(k,1,1,n,l,r)) zrj++;
      printf("%d\n",zrj);
    }
  }
  return 0;
}

3. 洛谷P2068 统计和

题目描述

给定一个长度为\(n（n \leq 100000）\)，初始值都为\(0\)的序列，\(x(x \leq 10000)\)次的修改某些位置上的数字，每次加上一个数，然后提出\(y (y \leq 10000)\)个问题，求每段区间的和。时间限制\(1\)秒。

输入输出格式

输入格式：

第一行\(1\)个数，表示序列的长度\(n\)

第二行\(1\)个数，表示操作的次数\(w\)

后面依次是\(w\)行，分别表示加入和询问操作

其中，加入用\(x\)表示，询问用\(y\)表示

\(x\)的格式为"\(x\) \(a\) \(b\)" 表示在序列\(a\)的位置加上\(b\)

\(y\)的格式为"\(y\) \(a\) \(b\)" 表示询问\(a\)到\(b\)区间的加和

输出格式：

每行一个数，分别是每次询问的结果

输入输出样例

输入样例#1：

5
4
x 3 8
y 1 3
x 4 9
y 3 4

输出样例#1：

8
17

思路：一道(线段树&树状数组)的(单点修改&区间查询)的板子题，不用过多解释……

代码：

#include<cstdio>
#include<algorithm>
#define maxn 100007
#define lb(x) x&(-x)
using namespace std;
int n,m,a[maxn];
char s[2];
inline void add(int x, int w) {
  while(x<=n) {
    a[x]+=w;
    x+=lb(x);
  }
} 
inline int csum(int x) {
  int ans=0;
  while(x) {
    ans+=a[x];
    x-=lb(x);
  }
  return ans;
}
int main() {
  scanf("%d%d",&n,&m);
  for(int i=1,l,r;i<=m;++i) {
    scanf("%s%d%d",s,&l,&r);
    if(s[0]=='x') add(l,r);
    else printf("%d\n",csum(r)-csum(l-1));
  }
  return 0;
}

4. 洛谷P2184 贪婪大陆

题目背景

面对蚂蚁们的疯狂进攻，小FF的\(Tower\) \(defence\)宣告失败……人类被蚂蚁们逼到了\(Greed\) \(Island\)上的一个海湾。现在，小FF的后方是一望无际的大海， 前方是变异了的超级蚂蚁。 小FF还有大好前程，他可不想命丧于此， 于是他派遣手下最后一批改造\(SCV\)布置地雷以阻挡蚂蚁们的进攻。

题目描述

小FF最后一道防线是一条长度为\(N\)的战壕， 小FF拥有无数多种地雷，而\(SCV\)每次可以在\([ L , R ]\)区间埋放同一种不同于之前已经埋放的地雷。 由于情况已经十万火急，小FF在某些时候可能会询问你在\([ L' , R']\)区间内有多少种不同的地雷， 他希望你能尽快的给予答复。

对于\(30\%\)的数据： \(0 \leq n, m \leq 1000\);

对于\(100\%\)的数据： \(0 \leq n, m \leq 10^5\).

输入输出格式

输入格式：

第一行为两个整数\(n\)和\(m\)； \(n\)表示防线长度， \(m\)表示\(SCV\)布雷次数及小FF询问的次数总和。

接下来有\(m\)行， 每行三个整数\(Q，L , R\)； 若\(Q=1\) 则表示\(SCV\)在\([ L , R ]\)这段区间布上一种地雷， 若\(Q=2\)则表示小FF询问当前\([ L , R ]\)区间总共有多少种地雷。

输出格式：

对于小FF的每次询问，输出一个答案（单独一行），表示当前区间地雷总数。

输入输出样例

输入样例#1：

5 4
1 1 3
2 2 5
1 2 4
2 3 5

输出样例#1：

1
2

思路：考虑一种容斥的思想，就是一段区间\(l\)到\(r\)的地雷种类就是\(r\)之前的埋地雷操作时的左端点数量减去\((l-1)\)之前的埋地雷操作时的右端点数量，这种关系可以自己画图得来，然后求左右端点的数量可以用线段树或树状数组来维护。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 100007
#define lb(x) x&(-x)
using namespace std;
int n,m,a[maxn],b[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
inline void add1(int x, int w) {
  while(x<=n) {
    a[x]+=w;
    x+=lb(x);
  }
}
inline void add2(int x, int w) {
  while(x<=n) {
    b[x]+=w;
    x+=lb(x);
  }
}
inline int csum1(int x) {
  int ans=0;
  while(x) {
    ans+=a[x];
    x-=lb(x);
  }
  return ans;
}
inline int csum2(int x) {
  int ans=0;
  while(x) {
    ans+=b[x];
    x-=lb(x);
  }
  return ans;
}
int main() {
  n=qread(),m=qread();
  for(int i=1,k,l,r;i<=m;++i) {
    k=qread(),l=qread(),r=qread();
    if(k==1) add1(l,1),add2(r,1);
    else printf("%d\n",csum1(r)-csum2(l-1));
  }
  return 0;
}

5. P2846 光开关Light Switching

题目描述

灯是由高科技——外星人鼠标操控的。你只要左击两个灯所连的鼠标，

这两个灯，以及之间的灯都会由暗变亮，或由亮变暗。右击两个灯所连的鼠

标，你就可以知道这两个灯，以及之间的灯有多少灯是亮的。起初所有灯都是暗的，你的任务是在\(LZ\)之前算出灯的亮灭。

输入输出格式

输入格式：

第1 行: 用空格隔开的两个整数\(N\) 和\(M\)，\(N\) 是灯数

第\(2..M+1\) 行: 每行表示一个操作, 有三个用空格分开的整数: 指令号, \(S_i\) 和\(E_i\)

第\(1\) 种指令(用\(0\) 表示)包含两个数字\(S_i\) 和\(E_i\) (\(1 \leq S_i \leq E_i \leq N\)), 它们表示起

始开关和终止开关. 表示左击

第\(2\) 种指令(用\(1\) 表示)同样包含两个数字\(S_i\) 和\(E_i\) (\(1 \leq S_i \leq E_i \leq N\)), 不过这

种指令是询问从\(S_i\) 到\(E_i\) 之间的灯有多少是亮着的.

输出格式：

输入输出样例

输入样例#1：

4 5
0 1 2
0 2 4
1 2 3
0 2 4
1 1 4

输出样例#1：

1
2

说明

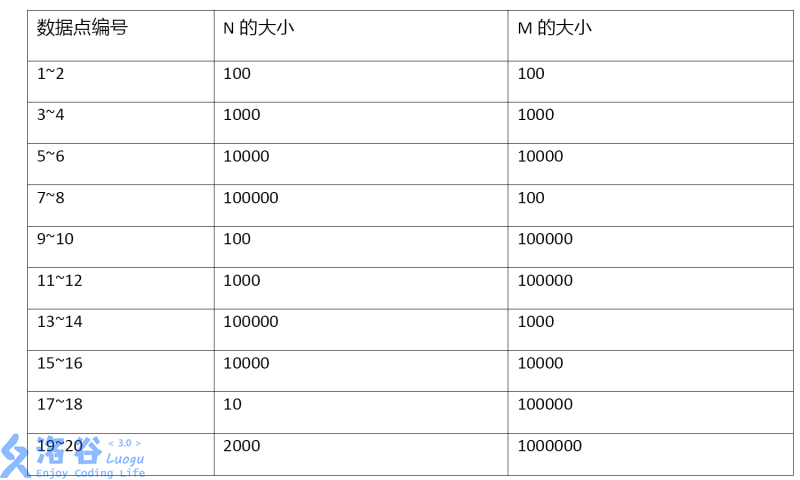
思路：这道题目涉及到区间修改和区间查询，因此可以用线段树来维护，那该怎么维护呢？继续观察，可以发现，因为刚开始所以灯都是关着的，然后修改一次就灯的状态就会变化一次，我们可以用\(1\)和\(0\)分别代替开关状态，那么修改操作不就成了区间异或运算么？查询操作不就成了查询区间中\(1\)的个数了么？而且初始值都是0，所以无需建树，然后用线段树维护一个区间\(1\)的个数即可。

代码：

#include<cstdio>
#include<algorithm>
#include<cctype>
#define maxn 100007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int n,m,sum[maxn<<2],lazy[maxn<<2];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
inline void pushup(int rt) {
  sum[rt]=sum[ls]+sum[rs];
}
inline void pushdown(int rt, int len) {
  if(lazy[rt]) {
    lazy[ls]^=1;
    lazy[rs]^=1;
    sum[ls]=(len-(len>>1))-sum[ls];
    sum[rs]=(len>>1)-sum[rs];
    lazy[rt]=0;
  }
}
void modify(int rt, int l, int r, int L, int R) {
  if(L>r||R<l) return;
  if(L<=l&&r<=R) {
    sum[rt]=r-l+1-sum[rt];
    lazy[rt]^=1;
    return;
  }
  pushdown(rt,r-l+1);
  int mid=(l+r)>>1;
  modify(ls,l,mid,L,R),modify(rs,mid+1,r,L,R);
  pushup(rt);
}
int csum(int rt, int l, int r, int L, int R) {
  if(L>r||R<l) return 0;
  if(L<=l&&r<=R) return sum[rt];
  pushdown(rt,r-l+1);
  int mid=(l+r)>>1;
  return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
int main() {
  n=qread(),m=qread();
  for(int i=1,k,l,r;i<=m;++i) {
    k=qread(),l=qread(),r=qread();
    if(!k) modify(1,1,n,l,r);
    else printf("%d\n",csum(1,1,n,l,r));
  }
  return 0;
}

6. 洛谷P2574 XOR的艺术

题目描述

\(AKN\)觉得第一题太水了，不屑于写第一题，所以他又玩起了新的游戏。在游戏中，他发现，这个游戏的伤害计算有一个规律，规律如下

1、 拥有一个伤害串为长度为\(n\)的\(01\)串。

2、 给定一个范围\([l,r]\)，伤害为伤害串的这个范围内中\(1\)的个数

3、 会被随机修改伤害串中的数值，修改的方法是把\([l,r]\)中的所有数\(xor\)上\(1\)

\(AKN\)想知道一些时刻的伤害，请你帮助他求出这个伤害

输入输出格式

输入格式：

第一行两个数\(n,m\),表示长度为\(n\)的\(01\)串，有\(m\)个时刻

第二行一个长度为\(n\)的\(01\)串，为初始伤害串

第三行开始\(m\)行，每行三个数\(p,l,r\)

若\(p\)为\(0\)，则表示当前时刻改变\([l,r]\)的伤害串，改变规则如上

若\(p\)为\(1\)，则表示当前时刻\(AKN\)想知道\([l,r]\)的伤害

输出格式：

对于每次询问伤害，输出一个数值伤害，每次询问输出一行

输入输出样例

输入样例#1：

10 6
1011101001
0 2 4
1 1 5
0 3 7
1 1 10
0 1 4
1 2 6

输出样例#1：

3
6
1

说明

样例解释：

\(1011101001\)

\(1100101001\)

询问\([1,5]\)输出\(3\)

\(1111010001\)

询问\([1,10]\)输出\(6\)

\(0000010001\)

询问\([2,6]\)输出\(1\)

数据范围：

\(10\%\)数据\(2≤n,m≤10\)

另有\(30\%\)数据\(2≤n,m≤2000\)

\(100\%\)数据\(2≤n,m≤2*10^5\)

思路：这是一道跟洛谷\(P2574\)思路类似的一道题目，唯一不同的就是这道题需要建树，因为初始值不都是\(0\)，然后对于此题，区间修改操作就是区间异或运算，区间查询就是查询区间中\(1\)的个数，然后用线段树维护区间中\(1\)的个数即可。

代码：

#include<cstdio>
#include<cctype>
#define maxn 200007
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
int n,m,sum[maxn<<2],lazy[maxn<<2];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
inline void pushup(int rt) {
  sum[rt]=sum[ls]+sum[rs];
}
void build(int rt, int l, int r) {
  if(l==r) {
    scanf("%1d",&sum[rt]);
    return;
  }
  int mid=(l+r)>>1;
  build(ls,l,mid);
  build(rs,mid+1,r);
  pushup(rt);
}
inline void pushdown(int rt, int len) {
  if(lazy[rt]) {
    lazy[ls]^=1;
    lazy[rs]^=1;
    sum[ls]=(len-(len>>1))-sum[ls];
    sum[rs]=(len>>1)-sum[rs];
    lazy[rt]=0;
  }
}
void modify(int rt, int l, int r, int L, int R) {
  if(L>r||R<l) return;
  if(L<=l&&r<=R) {
    lazy[rt]^=1;
    sum[rt]=r-l+1-sum[rt];
    return;
  }
  pushdown(rt,r-l+1);
  int mid=(l+r)>>1;
  modify(ls,l,mid,L,R),modify(rs,mid+1,r,L,R);
  pushup(rt);
}
int csum(int rt, int l, int r, int L, int R) {
  if(L>r||R<l) return 0;
  if(L<=l&&r<=R) return sum[rt];
  pushdown(rt,r-l+1);
  int mid=(l+r)>>1;
  return csum(ls,l,mid,L,R)+csum(rs,mid+1,r,L,R);
}
int main() {
  n=qread(),m=qread();
  build(1,1,n);
  for(int i=1,k,l,r;i<=m;++i) {
    k=qread(),l=qread(),r=qread();
    if(!k) modify(1,1,n,l,r);
    else printf("%d\n",csum(1,1,n,l,r));
  }
  return 0;
}