GAN理论推导

在知乎上看到一个对GAN推导得十分仔细的文章，写得非常好，我准备按照他的思路推导一下GAN的理论。可以理解为这篇文章转载自：https://zhuanlan.zhihu.com/p/27295635

GAN的原理

首先我们知道真实图片集的分布 $P_{d a t a} (x)$ ，x是一个真实的图片，可以想象为一个向量，这个向量集合的分布就是 $P_{d a t a}$ 。我们现在有Generator生成的分布假设为 $p_{G} (x; θ)$ ，这是一个由 $θ$ 控制的分布， $θ$ 是这个分布的参数(如果是高斯混合模型，那么 $θ$ 就是每个高斯分布的平均值和方差)，假设我们再真实分布中取一些数据， $x^{1}, x^{2}, . . ., X^{m}$ ，我们想要计算一个似然 $P_{G} (x^{i}; θ)$ ，关于似然的理解可以参考这篇博客：https://blog.csdn.net/weixin_40499753/article/details/82977623 对于这些数据，在生成模型中的似然就是 $L = \prod_{i = 1}^{m} P_{G} (x^{i}; θ)$ ，我们想要最大化这个似然，等价于让generator生成那些真实图片的概率最大，这就变成了一个最大似然估计的问题了，我们需要找到一个参数 $θ^{*}$ 来最大化这个似然。公式推导如下：
$\begin{align} \theta ^* &= arg\ \max_{\theta}\prod_{i=1}^{m}P_G(x^i;\theta) \\ &=arg\ \max_{\theta}\ log\prod_{i=1}^{m}P_G(x^i;\theta) \\ &=arg\ \max_{\theta} \sum_{i=1}^{m}logP_G(x^i;\theta) \\ & \approx arg\ \max_{\theta}\ E_{x\sim P_{data}}[logP_G(x;\theta)] \\ & = arg\ \max_{\theta}\int_{x} P_{data}(x)logP_G(x;\theta)dx - \int_{x}P_{data}(x)logP_{data}(x)dx \\ &=arg\ \max_{\theta}\int_{x}P_{data}(x)(logP_G(x;\theta)-logP_{data}(x))dx \\ &=arg\ \min_{\theta}\int_{x}P_{data}(x)log \frac{P_{data}(x)}{P_G(x;\theta)}dx \\ &=arg\ \min_{\theta}\ KL(P_{data}(x)||P_G(x;\theta)) \end{align}$ 我们寻找一个 $θ^{*}$ 来最大化这个似然，等价于最大化log似然。因为此时这m个数据是从真实分布中取得，所以也就约等于真实分布中的所有x在 $P_{G}$ 分布中的log似然的期望。真实分布中的所有x的期望，等价于求概率积分，可以转化为积分运算，因为减号后面的项和 $θ$ 无关，所以添加上之后还是等价的。然后提出共有的项，括号内的反转,max变为min，就可以转化为KL散度的形式了，KL散度描述的是2个向量之间的差异。所以最大化似然，让generator最大概率的生成真实图片，也就是要找一个 $θ$ 让 $P_{G}$ 更接近于 $P_{d a t a}$ ，那如何来找这个最合理的 $θ$ 呢？我们可以假设 $P_{G} (x; θ)$ 是一个神经网络。首先随机一个向量z，通过G(z)=x这个网络生成图片x，那么如何比较两个分布是否相似呢？只要我们取一组sample z，这组z符合一个分布，那么通过网络就可以生成另外一个分布 $P_{G}$ ，然后来和真实分布 $P_{d a t a}$ 比较。
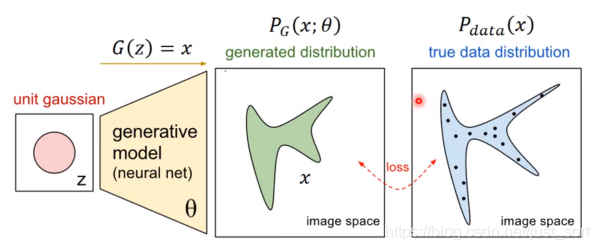在这里插入图片描述如何来找更接近的分布，这就是GAN的核心贡献了。GAN的公式为： $V(G,D)=E_{x\sim P_{data}}[logD(x)] + E_{x\sim P_G}[log(1-D(x))]$ 这个式子的好处在于，固定G，max V(G, D)就表示 $P_{G}$ 和 $P_{d a t a}$ 之间的差异，然后要找一个最好的G，让这个最大值最小，也就是2个分布之间的差异最小。 $G^*=arg\ \min_{G}\ \max_D\ V(G,D)$ 表面上看这个的意思是，D要让这个式子尽可能的大，也就是对于x是真实分布中，D(x)要接近与1，对于x来自于生成的分布，D(x)要接近于0，然后G要让式子尽可能的小，让来自于生成分布中的x，D(x)尽可能的接近1。
现在我们先固定G，来求解最优的D：
对于一个给定的x，得到最优的D如上图，范围在(0,1)内，把最优的D带入 $\max_D\ V(G,D)$ 可以得到：
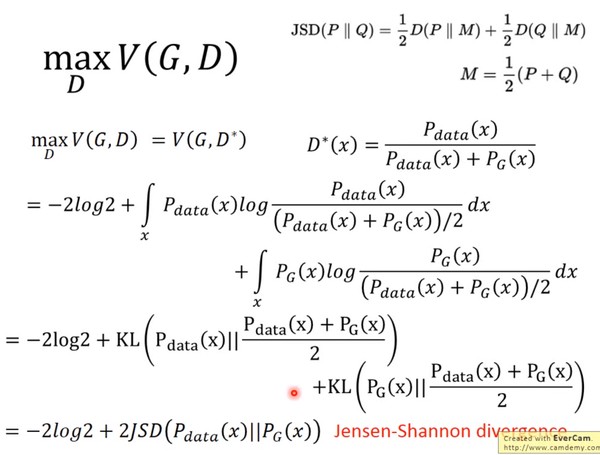
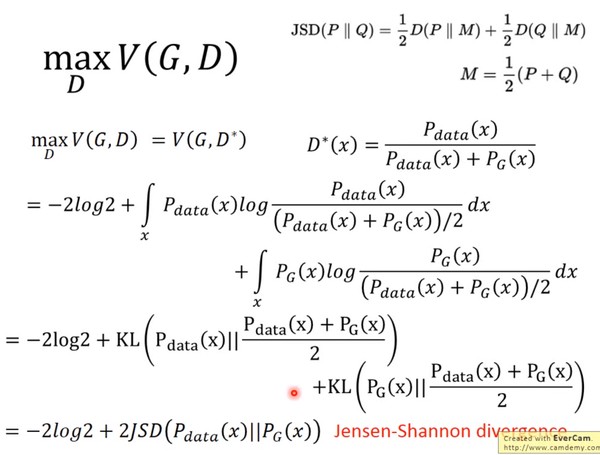JS divergence是KL divergence的对称平滑版本，表示了两个分布之间的差异，这个推导就表明了上面所说的，固定G, $\max_D\ V(G,D)$ 表示两个分布之间的差异，最小值是-2log2，最大值为0。现在我们需要找个G，来最小化 $\max_D\ V(G,D)$ 观察上式,当 $P_G(x)=P_{data}(x)$ 时，G是最优的。

训练

有了上面推导的基础之后，我们就可以开始训练GAN了。结合我们开头说的，两个网络交替训练，我们可以在起初有一个 $G_{0}$ 和 $D_{0}$ ，先训练 $D_{0}$ 找到 $\max_D\ V(G_0,D_0)$ ，然后固定 $D_{0}$ 开始训练 $G_{0}$ ，训练的过程都可以使用gradient descent，以此类推，训练 $D_{1}, G_{1}, D_{2}, G_{2} . . .$
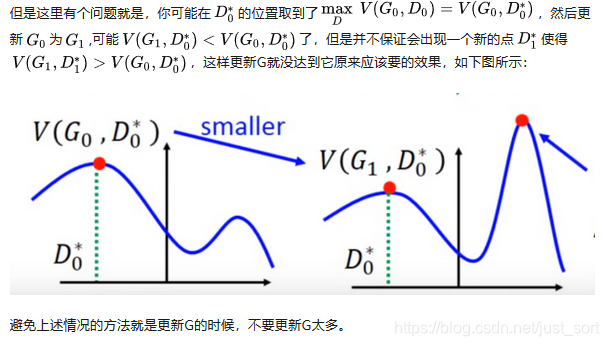在这里插入图片描述避免上述情况的方法就是更新G的时候，不要更新G太多。

知道了网络的训练顺序，我们还需要设定两个loss function，一个是D的loss，一个是G的loss。下面是整个GAN的训练具体步骤：
在这里插入图片描述上述步骤在机器学习和深度学习中也是非常常见，易于理解。

存在的问题

但是上面G的loss function还是有一点小问题，下图是两个函数的图像：
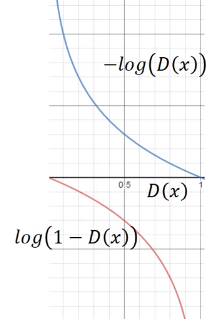在这里插入图片描述 $l o g (1 - D (x))$ 是我们计算时G的loss function，但是我们发现，在D(x)接近于0的时候，这个函数十分平滑，梯度非常的小。这就会导致，在训练的初期，G想要骗过D，变化十分的缓慢，而上面的函数，趋势和下面的是一样的，都是递减的。但是它的优势是在D(x)接近0的时候，梯度很大，有利于训练，在D(x)越来越大之后，梯度减小，这也很符合实际，在初期应该训练速度更快，到后期速度减慢。
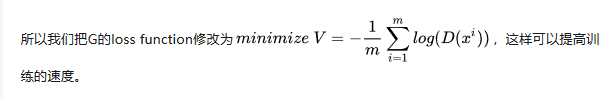
在这里插入图片描述还有可能的原因是，虽然两个分布都是高维的，但是两个分布都十分的窄，可能交集相当小，这样也会导致JS divergence算出来=log2，约等于没有交集。解决的一些方法，有添加噪声，让两个分布变得更宽，可能可以增大它们的交集，这样JS divergence就可以计算，但是随着时间变化，噪声需要逐渐变小。
还有一个问题叫Mode Collapse，如下图：
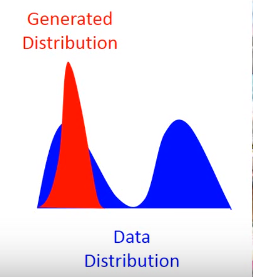在这里插入图片描述这个图的意思是，data的分布是一个双峰的，但是学习到的生成分布却只有单峰，我们可以看到模型学到的数据，但是却不知道它没有学到的分布。

造成这个情况的原因是，KL divergence里的两个分布写反了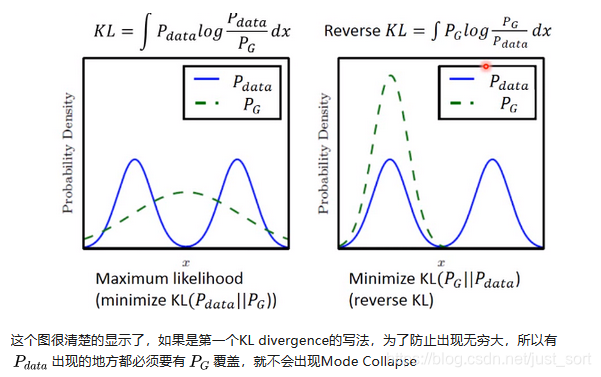，在这里插入图片描述

GAN理论推导（知乎转载）

GAN理论推导

GAN的原理

训练

存在的问题