描述
题目描述
首先我们先介绍一下这个LFU缓存结构在这个题目里面是如何考察的
首先他是有两个功能,第一个功能就是插入
那么我们这个功能要插入的是一个键值对,这里题目有地方描述的不是太清楚,这里我们默认他插入的时候,如果以前存在这个键值key,我们进行更新,如果不存在的话,我们再进行插入,然后插入有一个要求就是,不能超过我们的一个容量,如果超过了我们的容量,那么我们要删掉被调用最少的那个键值对,如果有多个最少的话,我们删掉进入我们这个缓存结构中最早的那个
然后第二个功能查找
要查找某一个key对应的val值,这个我们可以直接用封装好的map实现
这两个操作都需要更新调用次数
题解
解法一
实现思路
这里我们要保证一个顺序,就是我们出现的时间和使用的次数的这么一个顺序,那么我们可以用封装好的平衡二叉树set使用,然后我们这里可以使用一个哈希表来存储这些键值对的映射关系,然后我们开辟一个缓存结构来定义一种数据类型来被我们的set使用
然后对于两种不同的操作,比如对于查找,我们只要看有没有就可以了,有的话就直接返回,没有的话就返回-1,然后更新时间和使用次数
对于插入,我们判断这个key以前有没有,如果以前有的话,我们更新,没有的话我们插入,同时不忘记更新使用时间和次数,这里要考虑一个缓存容量的问题,又因为我们定了一种缓存结构,运算符重载了小于号,所以我们set直接删除第一个就可以了
代码实现
class Solution {
struct node {
int cnt, time, key, val;
node(int _cnt, int _time, int _key, int _val)
: cnt(_cnt), time(_time), key(_key), val(_val) {}
bool operator<(const node& wa) const {
return cnt == wa.cnt ? time < wa.time : cnt < wa.cnt;
}
// 经典的重载运算符,当然如果用lambda也是可以的
};
unordered_map<int, node> mp;
set<node> st;
int time = 0;
public:
int get(int key, int k) {
if (k == 0) return -1;
auto it = mp.find(key);
if (it == mp.end()) return -1;
// 判断有无这个键值
node tmp = it->second;
st.erase(tmp);
tmp.cnt++;
tmp.time = ++time;
st.insert(tmp);
// 更新我们的缓存
// 这里涉及到了一个删除旧的换上新的一个过程
it->second = tmp;
return tmp.val;
}
void put(int key, int val, int k) {
if (k == 0) return;
auto it = mp.find(key);
if (it == mp.end()) {
if (mp.size() == k) {
// 从哈希表和平衡二叉树中删除最近最少使用的缓存
mp.erase(st.begin()->key);
st.erase(st.begin());
}
// 创建新的缓存
node cache = node(1, ++time, key, val);
// 将新缓存放入哈希表和平衡二叉树中
mp.insert(make_pair(key, cache));
st.insert(cache);
} else {
// 如果我们以前有这个键值,那么我们直接更新一下就可以了
node tmp = it->second;
st.erase(tmp);
tmp.cnt += 1;
tmp.time = ++time;
tmp.val = val;
st.insert(tmp);
it->second = tmp;
// 把旧的去除掉,然后换成我们新的
}
}
vector<int> LFU(vector<vector<int> >& operators, int k) {
vector<int> res;
for (auto &it : operators) {
if (it.size() == 2) {
// 执行取出操作
res.emplace_back(get(it[1], k));
} else {
// 执行插入操作
put(it[1], it[2], k);
}
}
return res;
}
};
时间复杂度分析
时间复杂度:
理由如下: 我们的时间复杂度的瓶颈在于我们对平衡二叉树的操作每次是的, 然后我们进行了次
空间复杂度:
理由如下: 跟我们缓存容量有关系, 我们的数据结构存储的内容无法超过我们的缓存大小
解法二:双哈希
实现思路
这里我们既然想要每次都是的操作,那么我们这里可以使用一种哈希表的操作,我们发现我们可以把每个频率放入跟这个频率相同的节点,如图所示
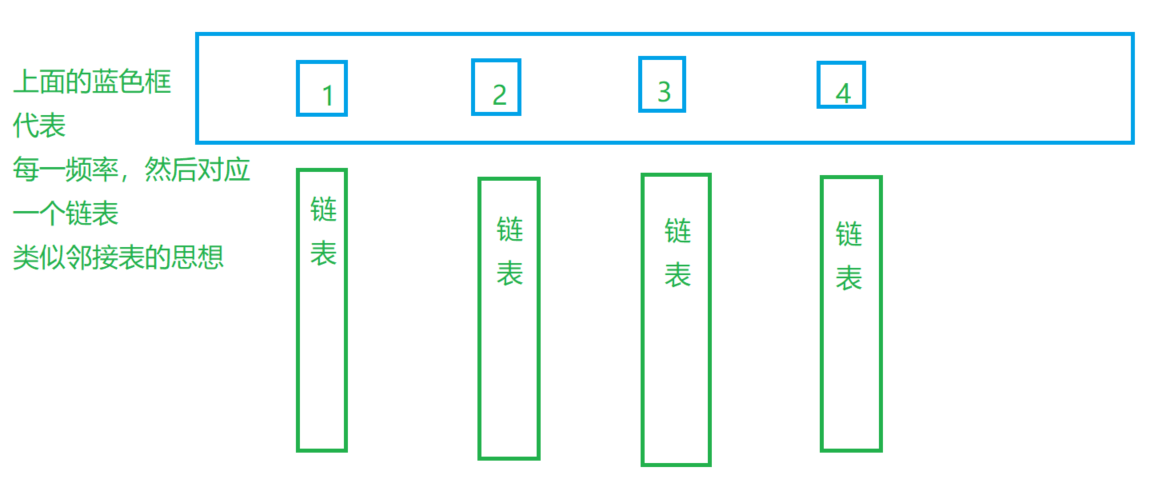
然后我们对于每一个都可以找到对应的一个,那么我们就直接进行一个哈希的对应,如图所示
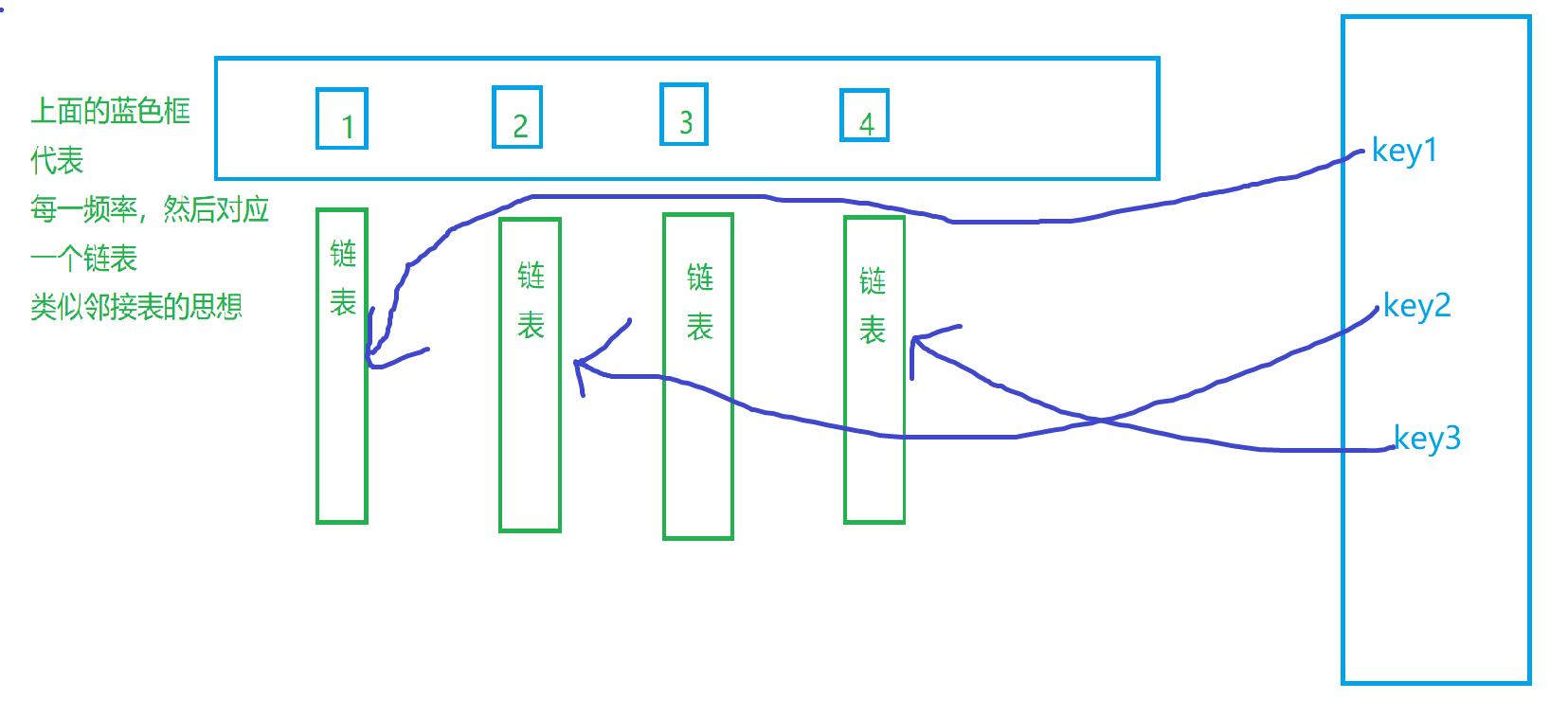
右侧的是我们的的哈希表,这样我们就明确了思路,开始进行一个代码的实现
代码实现
class Solution {
struct node {
int key, val, cnt;
// cnt代表的使用频率
node() {}
node(int _key, int _val, int _cnt) : key(_key), val(_val), cnt(_cnt) {}
// 我们编写一下构造函数
};
unordered_map<int, list<node>::iterator> keyToVal;
unordered_map<int, list<node>> cntToVal;
// 这里是我们一个是key对val的哈希表,一个是频率的哈希表
int minnCnt = 0;
public:
void set(int key, int val, int k) {
if (k == 0) return;
auto it = keyToVal.find(key);
if (it == keyToVal.end()) {
// 缓存满了
if (keyToVal.size() == k) {
auto it2 = cntToVal[minnCnt].back();
keyToVal.erase(it2.key);
// 取得最末尾的点然后删除
cntToVal[minnCnt].pop_back();
if (cntToVal[minnCnt].size() == 0) {
cntToVal.erase(minnCnt);
}
}
cntToVal[1].push_front(node(key, val, 1));
keyToVal[key] = cntToVal[1].begin();
minnCnt = 1;
// 重新放入新的点,然后更新我们的末尾点的位置
return;
}
list<node>::iterator tmp = it->second;
int ccnt = tmp->cnt;
cntToVal[ccnt].erase(tmp);
if (cntToVal[ccnt].size() == 0) {
cntToVal.erase(ccnt);
if (minnCnt == ccnt) minnCnt++;
}
cntToVal[minnCnt + 1].push_front({key, val, ccnt + 1});
keyToVal[key] = cntToVal[ccnt + 1].begin();
// 更新需要更新的缓存值
}
int get(int key, int k) {
if (k == 0) return -1;
auto it = keyToVal.find(key);
if (it == keyToVal.end()) return -1;
list<node>::iterator tmp = it->second;
int val = tmp->val, ccnt = tmp->cnt;
// 如果当前的链表空的,我们在哈希表中删掉
cntToVal[ccnt].erase(tmp);
if (cntToVal[ccnt].size() == 0) {
cntToVal.erase(ccnt);
if (minnCnt == ccnt) minnCnt++;
}
// 插入到我们频率加一的下一个位置
cntToVal[ccnt + 1].push_front(node(key, val, ccnt + 1));
keyToVal[key] = cntToVal[ccnt + 1].begin();
return val;
}
vector<int> LFU(vector<vector<int>>& operators, int k) {
vector<int> res;
for (auto &it : operators) {
if (it.size() == 2) {
// 执行取出操作
res.emplace_back(get(it[1], k));
} else {
// 执行插入操作
set(it[1], it[2], k);
}
}
return res;
}
};
时空复杂度分析
时间复杂度:
理由如下:我们有次操作,每次操作的时间是
空间复杂度:
理由如下: 跟我们缓存容量有关系, 我们的数据结构存储的内容无法超过我们的缓存大小
写在最后
事实上,我们觉得这个是哈希表,这个没有问题,但是实际他的效率并不高
第一个问题
这个容器有如果用在算法竞赛是有很大问题的,首先他的哈希模数是固定的,在以及之前他的哈希模数都是,在以及之后哈希模数都是,所以如果我们想让这个容器退化,那么我们只要根据编译器的版本进行一个哈希碰撞,我们让他每次都需要重新分配空间,他每一次操作就变成了,然后如果我们有次操作,那么时间复杂度就变成了,所以这个并不是很优秀
第二个问题
这个容器速度并不是很快,他的本质均摊下来是的,但是事实上他的常数非常的大,他的常数已经是接近级别的,常数这个概念是我们计算复杂度的时候会忽略较小的常数,比如一个有一个循环,另一个十个循环并列,都是的复杂度,事实上一个运行了一次,一个运行了十次,可以这样简单理解,所以事实上这个容器常数很大,那么并不是很快,当我们的数据范围达到千万级别时候,它和它才会更快一点






 京公网安备 11010502036488号
京公网安备 11010502036488号