LeetCode 第四题 Median of Two Sorted Arrays 二人 渣渣选手乱七八糟分析发现基本回到思路1

题目

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0
Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5
一句话题意，用 $O\left(lo{g}_2\right(n+m\left)\right)$O(log2​(n+m))的时间复杂度找出两个数组中的数的中位数。

思路

思路1——直接合并

求中位数说白了就是要找第k大数。
偶数个k有两个取值，奇数k一个取值。
最简单的做法是直接“合并”数组。但是这种做法——
$T=O(n+m)M=O\left(1\right)$T=O(n+m)M=O(1)
所以，必然不能合并。
根据复杂度可以猜测是需要用到二分。

思路2——定位两个数组的中间元素，二分

直接定位两个数组的中间元素x和y(下标为数组长度整除2).
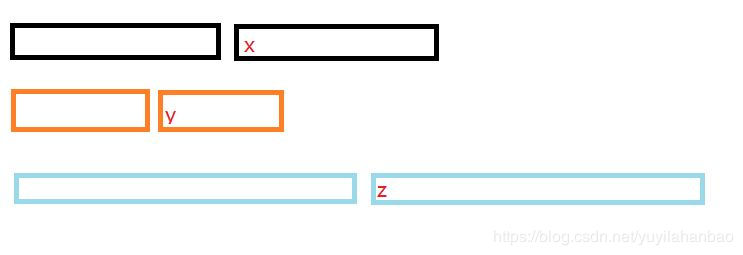
示意图如下——
黑色和橙色分别为输入的两个数组。
蓝色是虚拟的两个数组合并后的数组。
每个数组都分为了左右两个长度大致相当的两部分（偶数时相同，奇数时有部分多一个数）。
方框中的字母代表这一部分的第一个元素。

暂时不细致的考虑边界情况，粗略的叙述。
对于x，如果x落在蓝左，则大致可以淘汰黑左，否则可以淘汰黑右.
对于y，如果y落在橙左，则大致可以淘汰橙左，否则可以淘汰橙右.
如此，规模总的缩小为原来的二分之一。
然而，这就需要解决一个问题——
在橙色数组中比x小的元素有多少个。
解决了这个问题就可以确定x在蓝色中的位置。
这个问题可以使用二分解决， $O\left(lo{g}_{2}m\right)$O(log2​m)
如此 $T(n,m)=O\left(lo{g}_{2}m\right)+O\left(lo{g}_{2}n\right)+T(n/2,m/2)$T(n,m)=O(log2​m)+O(log2​n)+T(n/2,m/2)
这个的复杂度我不会算了，但我估计是超过了 $O\left(lo{g}_2\right(n+m\left)\right)$O(log2​(n+m)).

思路3——利用不等式的传递性

在思路2中，我们是用x,y各自淘汰其所在数组的一半元素。
其实是分了两步，而且这两部其实是各自独立，互不相关的。
要达到 $O\left(lo{g}_2\right(n+m\left)\right)$O(log2​(n+m))的复杂度，需要我们把问题缩小为原来规模的一半，
但在思路2中我们忽略了不等式的传递性。
为了叙述方便，而且这只是思路，因此下面的不怎么考虑不能除尽、取整的边界问题。

不妨设x<=y（否则可以交换一下两个数组的位置）
因此，可以确定黑左<=x<=y<=蓝右且黑左<=黑右
因此两个数组的右半部分都排在黑左的后面，我们黑左里面的排名的上限被确定了，里面的绝大多数元素可以淘汰（之所以不说全部是因为实际上要考虑边界情况）。因此考虑边界情况时，可以往前移动一下（最多移动1格还是2格）。
同理，橙右可以确定排名的下限，然后……
如此，我们O(1)的做到了问题规模缩小一半，复杂度解决了。
然而，个人感觉边界情况讨论起来有点头皮发麻，估计if语句不好写，代码不好写呀。

思路4——为何要两个数组都恰好各自分成相当的两块呢？

思路3中因为分成两半的情况涉及到奇数偶数的差异，两个组合起来情况有点多，我选择死亡。
但是注意到思路3中是利用不等式的传递性来确定排名上下限，而且淘汰掉的两部分刚好是对角的，那么为何不构造一种划分方法，避免边界情况讨论呢？

符号约定

A分成 $A_l,A_r$Al​,Ar​两部分，长度分别为 $l_a,r_a$la​,ra​
B分成 $B_l,B_r$Bl​,Br​两部分，长度分别为 $l_b,r_b$lb​,rb​
$A_l,B_l$Al​,Bl​最后一个元素是 $x_1,y_1$x1​,y1​
$A_r,B_r$Ar​,Br​第一个元素是 $x_2,y_2$x2​,y2​
$a_l$al​表示数组 $A_l$Al​中任意一个元素， $a_r,b_r,c_r$ar​,br​,cr​同理。
$rank\left(item\right)$rank(item)表示 $item$item在合并后的有序数组的下标(从0计)。

确定限定条件

$L_l=l_a+l_b,L_r=r_a+r_b$Ll​=la​+lb​,Lr​=ra​+rb​
$L=n+m=L_l+L_r$L=n+m=Ll​+Lr​

1. 若 $x_2{\le }_2$x2​≤2​
   利用不等式的传递性，得：
   $rank\left(a_l\right)\le rank\left(x_2\right)-1=L-L_r-1$rank(al​)≤rank(x2​)−1=L−Lr​−1
   $rank\left(b_r\right)\ge rank\left(y_2\right)\ge L_l$rank(br​)≥rank(y2​)≥Ll​
   寻找rank为k的元素，欲稳定的可以淘汰 $A_l,B_r$Al​,Br​
   ，则需要
   $L-1-L_r\&lt;k{L}_l\&gt;k$L−1−Lr​<kLl​>k
   得 $L_r\&gt;L-1-k{L}_l\&gt;k$Lr​>L−1−kLl​>k
   另外淘汰数是 $l_a+r_b$la​+rb​
2. 若 $x_2\ge y_2$x2​≥y2​
   同样有： $L_r\&gt;L-1-k{L}_l\&gt;k$Lr​>L−1−kLl​>k
   淘汰数是： $l_b+r_a$lb​+ra​
   为了稳定的将规模缩小为原来的一半，需要
   $l_a+r_b$la​+rb​, $l_b+r_a$lb​+ra​各占总规模的一半。
   不防令
   $l_a+r_b=p=L/2l_b+r_a=L-p$la​+rb​=p=L/2lb​+ra​=L−p
   上面的公式中出现的除号是整除，不是整除将会使用分号表示，后同
   因此，所有约束条件是：
   ①Lr​>L−1−k②Ll​>k③ra​+rb​=L/2

开始构造

不妨设 $n\&lt;=m$n<=m(否则交换)
取定 $l_a\in [0,n]$la​∈[0,n],则
$r_b=L/2-l_a=(n+m)/2-l_a\in [0,m].$rb​=L/2−la​=(n+m)/2−la​∈[0,m].
故 $l_a$la​确定, $l_b,r_a,r_b$lb​,ra​,rb​皆确定，且都是在所在数组长度范围内。
$L_l=l_a+l_b=l_a+m-r_b=l_a+m-(n+m)/2+l_a=2l_a+m-(n+m)/2$Ll​=la​+lb​=la​+m−rb​=la​+m−(n+m)/2+la​=2la​+m−(n+m)/2
代入②式得:
$l_a\&gt;\frac{k+(n+m)/2-m}{2}$la​>2k+(n+m)/2−m​
注意k的取值不是任意的，只有 $(n+m-1)/2$(n+m−1)/2与 $(n+m)/2$(n+m)/2两个取值，总长度相同时这两个取值一样。

1. 当总长度L为奇数， $l_a\&gt;\frac{n-1}{2}\Rightarrow l_a\&gt;(n-1)/2$la​>2n−1​⇒la​>(n−1)/2
2. 当总长度L为偶数，取前一个数为k, $l_a\&gt;\frac{n-1}{2}\Rightarrow l_a\&gt;(n-1)/2$la​>2n−1​⇒la​>(n−1)/2
3. 当总长度L为偶数，取后一个数为k, $l_a\&gt;\frac{n}{2}\Rightarrow l_a\&gt;n/2$la​>2n​⇒la​>n/2
   由于 $l_a$la​取值只能是整数,且是大于号，因此上面不等式的右边可以向下取整，可以直接换成整除号。

同理，对于①式的 $L_r$Lr​,可以得到：
$l_a\&lt;\frac{k+(n+m)/2-m+1}{2}$la​<2k+(n+m)/2−m+1​
4. 当总长度L为奇数， $l_a\&lt;\frac{n}{2}\Rightarrow l_a\&lt;(n+1)/2$la​<2n​⇒la​<(n+1)/2
5. 当总长度L为偶数，取前一个数为k, $l_a\&lt;\frac{n}{2}\Rightarrow l_a\&lt;(n+1)/2$la​<2n​⇒la​<(n+1)/2
6. 当总长度L为偶数，取后一个数为k, $l_a\&lt;\frac{n+1}{2}\Rightarrow l_a\&lt;(n+2)/2$la​<2n+1​⇒la​<(n+2)/2
由于 $l_a$la​取值只能是整数,且是小于号，因此上面三个式子的右边的数应该向上取整，可以分子加1再整除。
但是，目前很不幸的发现， $l_a$la​的上界和下界是相邻的两个整数，而且两不等号个都是不带等于的不等号，因此， $l_a$la​可取的值是空集。
把小于号换成小于于等于，即①式变成小于等于，一路追溯上去，只需要不淘汰 $x_1$x1​(或 $y_1$y1​)即可。
那么 $l_a$la​的取值：
$l_a=n/2+1总长度偶数，且k取后一个数$la​=n/2+1总长度偶数，且k取后一个数
其余情况 $l_a=(n+1)/2$la​=(n+1)/2
因排名小于k被淘汰掉的个数为 $l_a-1$la​−1,故 $k-=l_a-1$k−=la​−1
代码什么的下次再写

我现在发现求出来的结果和原本的直接两个数组两两对半分差别不大，心态有点崩。而且貌似这样子递归之后k就不是原本的总长度的一半了……
emmmm…
先O(n)暴力通过吧，另外膜拜一下discussion里的dalao解法

O(N)源码

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int l1 = nums1.length;
        int l2 = nums2.length;
        int l = l1 + l2;
        int nums[] = new int[l];
        int end = l/2+1;
        int i,j,k;
        i = j = k = 0;
        while (i < l1 && j < l2 && k < end) {
            if (nums1[i] < nums2[j])
                nums[k++] = nums1[i++];
            else
                nums[k++] = nums2[j++];
        }
        while (i < l1 && k < end)
            nums[k++] = nums1[i++];
        while (j < l2 && k < end)
            nums[k++] = nums2[j++];
        if (l%2 == 0)
            return (nums[l/2-1]+nums[l/2])/2.0;
        else
            return nums[l/2];
    }
}

Runtime: 26 ms, faster than 91.16% of Java online submissions for Median of Two Sorted Arrays.
Memory Usage: 49.7 MB, less than 100.00% of Java online submissions for Median of Two Sorted Arrays.

下次有时间在用discuss里面dalao的方法写一次。