https://ac.nowcoder.com/acm/contest/625/F
题意:有n个对子排,共 2∗n张,按照题目描述方法,选定最佳策略,求消除所有牌的期望轮数。
思路:
先说一下我在比赛时的错误,算是很经典的错误了吧。
我设 f(i,j):已经消除i对牌,已经记住j张孤立的牌的位置,达到这个状态的期望轮数。然后按照概率转移。
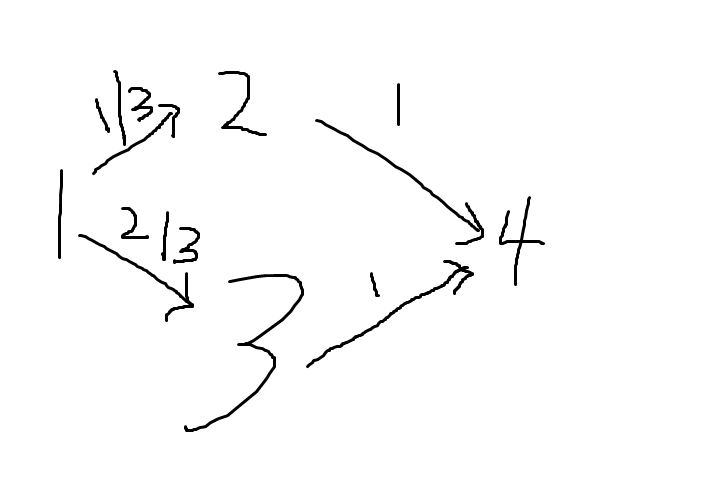
画个图就知道错在哪里了。
按照我的方法,到达2的期望步数是1/3,3是2/3,4是 (31+1)+(32+1)=3
这样是错误的。按照全期望公式:
Y是从u点到终点的期望,X是从u到终点的途径集合。
计算某一状态的期望,正确方法是考虑它转移到的状态的期望及其概率来计算它自己的期望。
回到上面的那张图,
应该设状态为 【当前在i,走到终点期望还需要几步】,然后逆推,而不是 【当前在i,期望已经走了几步】,然后顺推
这类问题的状态应该设计为【到达终点期望还需要多少步】,由终点推到起点
回到这个问题, f(i,j):应该设计为:
1.已经消除i对牌,已经记住j张孤立的牌的位置还需要的期望轮数。
2.或者还需要消除i对牌,已经记住j张孤立的牌的位置,还需要的期望轮数。
这两种的正确性都是没问题的
比赛时还有一个重大错误是:猜。因为样例给的是策略1,然后就把策略1当作正确策略,事实上,这是不一定的,应该两个都算之后比较
按照std的设计方法:设 f(n,m):还有n对(两个位置都不知道)以及m个(有一个不知道位置)待拼成,还需要的期望轮数
那么,令 hd=2∗n+m(未知位置个数)
策略1:本次翻一个已知位置一个未知位置(下面的已知未知说的是这种牌有没有翻出来(记住)过)
f(n,m)+=(f(n,m−1)+1)∗m∗hdm //两个已知,一样
f(n,m)+=(f(n,m−1)+2)∗m∗hdm∗(m−1) //两个已知,不一样
f(n,m)+=(f(n−1,m+1)+1)∗m∗hd2∗m∗n //一个已知,一个未知
策略2:本次翻两个未知位置(下面的已知未知说的是这种牌有没有翻出来(记住)过)
f(n,m)+=(f(n−1,m)+1)∗hd∗(hd−1)/2n //两个未知,一样
f(n,m)+=(f(n−2,m+2)+1)∗hd∗(hd−1)/2n∗(2n−1)−n //两个未知,不一样
f(n,m)+=(f(n−1,m)+2)∗hd∗(hd−1)/2m∗2∗n //一个未知,一个已知
f(n,m)+=(f(n,m−2)+3)∗hd∗(hd−1)/2m∗(m−1)/2 //两个已知
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define INF (1<<30)
double f[5005][5005];
double dfs(int n,int m)
{ //cout<<n<<" "<<m<<"\n";system("pause");
if(f[n][m]!=0)return f[n][m];
if(n==0&&m==0)return 0;
int hd=2*n+m;
f[n][m]=INF;
//m,hd策略
if(m>0)
{
double ans=0;
ans+=(dfs(n,m-1)+1)/hd;
if(m>=2)ans+=(dfs(n,m-1)+2)*(m-1)/hd;
if(n>0)ans+=(dfs(n-1,m+1)+1)*2*n/hd;
f[n][m]=min(f[n][m],ans);
}
//hd,hd策略
if(hd>=2)
{
double ans=0;
if(n>=1)ans+=(dfs(n-1,m)+1)*2*n/(hd*(hd-1));
if(n>=2)ans+=(dfs(n-2,m+2)+1)*(4*n*n-4*n)/(hd*(hd-1));
if(n>=1&&m>=1)ans+=(dfs(n-1,m)+2)*4*m*n/(hd*(hd-1));
if(m>=2)ans+=(dfs(n,m-2)+3)*m*(m-1)/(hd*(hd-1));
f[n][m]=min(f[n][m],ans);
}
return f[n][m];
}
int main()
{
//freopen("input.in","r",stdin);
int t,n;
cin>>t;
while(t--)
{
scanf("%d",&n);
printf("%.2f\n",dfs(n,0));
}
return 0;
}
最后又按比赛时类似的设计方法写了一遍
f(i,j):已经消除i对牌,已经记住j张孤立的牌的位置还需要的期望轮数。
比std略慢,测试了一下,dfs函数调用次数比std的要多,有点奇怪。
#include<bits/stdc++.h>
using namespace std;
#define INF (1<<30)
#define sum 5000
int T,n;
double f[5010][5010];
double dfs(int n,int m)
{
if(f[n][m])return f[n][m];
if(n==5000&&m==0)return 0;
f[n][m]=INF;
int hd=2*sum-2*n-m;
if(m>0)
{
double ans=0;
if(n<5000)ans+=(dfs(n+1,m-1)+1)/hd;
if(n<5000&&m>=2)ans+=(dfs(n+1,m-1)+2)*(m-1)/hd;
if(sum-n-m>=1)ans+=(dfs(n,m+1)+1)*2*(sum-n-m)/hd;
f[n][m]=min(f[n][m],ans);
}
if(hd>=2)
{
double ans=0;
int num=sum-n-m;
if(n<5000&&num>=1)ans+=(dfs(n+1,m)+1)*num/(hd*(hd-1)/2);
if(num>=2)ans+=(dfs(n,m+2)+1)*2*num*2*(num-1)/(hd*(hd-1));
if(n<5000&&m>=1)ans+=(dfs(n+1,m)+2)*m*2*num/(hd*(hd-1)/2);
if(n<=4998&&m>=2)ans+=(dfs(n+2,m-2)+3)*m*(m-1)/(hd*(hd-1));
f[n][m]=min(f[n][m],ans);
}
return f[n][m];
}
int main()
{
//freopen("input.in","r",stdin);
cin>>T;
while(T--)
{
scanf("%d",&n);
printf("%.2f\n",dfs(5000-n,0));
}
return 0;
}




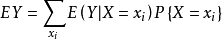

 京公网安备 11010502036488号
京公网安备 11010502036488号