正则表达式匹配
```java
public class Solution {
public boolean match(char[] str, char[] pattern)
{
int m = str.length;
int n = pattern.length;
boolean[][] dp = new boolean[m+1][n+1];
dp[0][0] = true;
for(int j =1;j<=n;j++){
if(pattern[j-1]=='*'){
dp[0][j] = dp[0][j-2];
}
}
for(int i =1;i<=m;i++){
for(int j =1;j<=n;j++){
if(str[i-1] ==pattern[j-1] || pattern[j-1]=='.'){
dp[i][j] = dp[i-1][j-1];
}else if(pattern[j-1]=='*'){
if(str[i-1] ==pattern[j-2] || pattern[j-2]=='.'){
dp[i][j] = (dp[i-1][j] || dp[i][j-1] ||dp[i][j-2]);
}else{
dp[i][j] = dp[i][j-2];
}
}
}
}
return dp[m][n];
}
}
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖整个字符串s的,而不是部分字符串。
**(注意这里零个是非常重要的,相当于把前面的抵消了)**
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
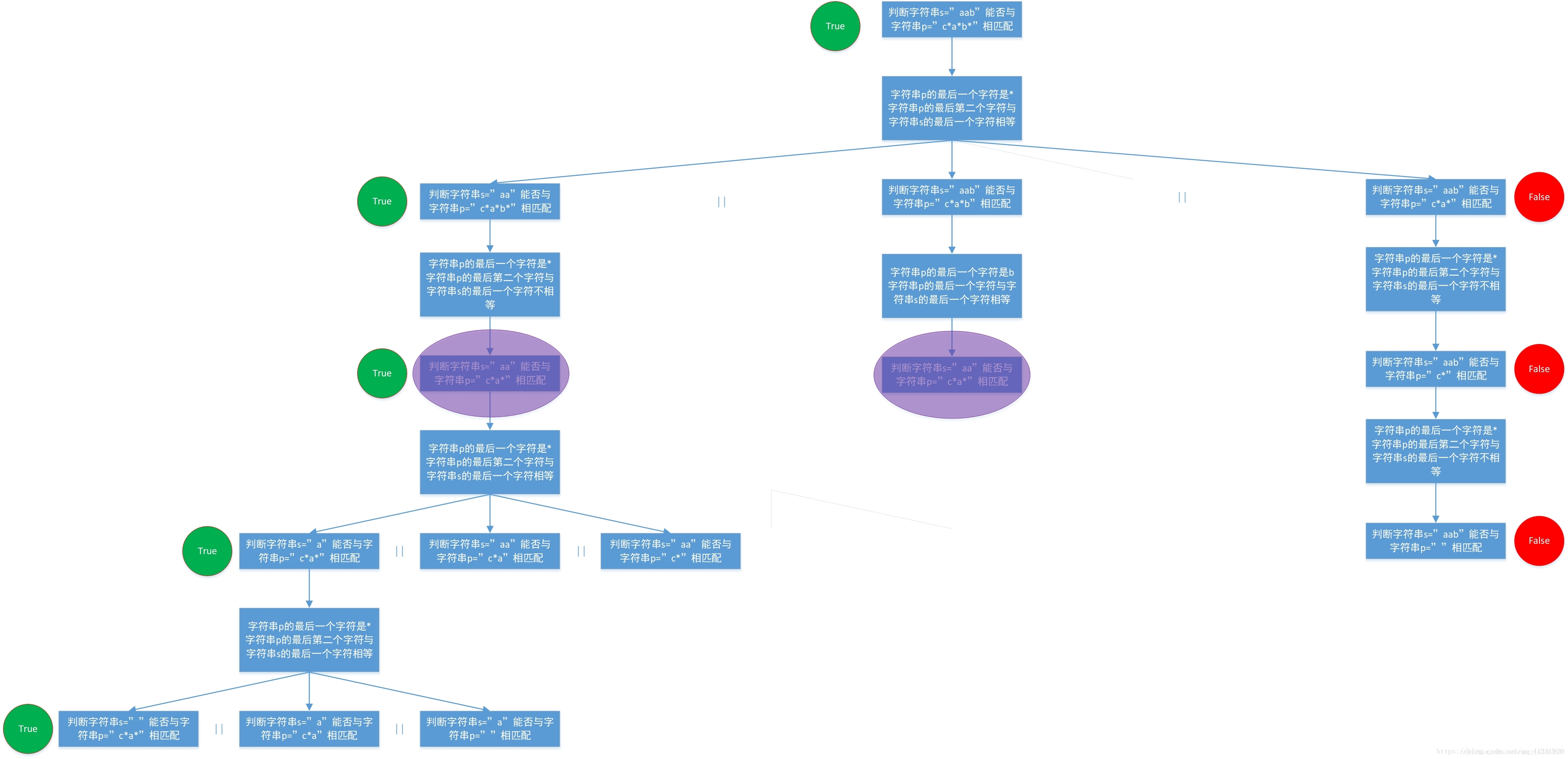
## 动态规划
重叠子问题,那么肯定就可以用动态规划来解决!而动态规划的关键是状态定义的合适选取以及发现正确的状态转移。
状态定义:
f(x, y)------字符串s中[0, x - 1]范围内的字符串能否匹配字符串p中[0, y - 1]范围内的字符串
状态转移:
(1)如果p(y) == '.', f(x, y) = f(x - 1, y - 1)。
(2)如果p(y) == s(x), f(x, y) = f(x - 1, y - 1)。
(3)如果p(y) == '※',
a.如果s(x) == p(y - 1) || p(y - 1) == '.',
a-1:使用'※号进行匹配——f(x - 1, y)
a-2:只使用'※'号前面的那个字符匹配,不使用'※'匹配——f(x, y - 1)
a-3:'※'号前面的那个字符在匹配的过程当中一个都不使用——f(x, y - 2)
f(x, y) = f(x - 1, y) || f(x, y - 1) || f(x, y - 2)。
b.如果s(x) != p(y - 1) && p(y - 1) != '.'
*号前面的那个字符在匹配的过程当中一个都不使用,f(x, y) = f(x, y - 2)。


为了处理s为空的情形,我们定义状态转移数组matched的行数和列数分别为s.length() + 1和p.length() + 1。显然我们有matched[0][0] = true。对于第0行,相当于字符串s为空,就是思路一中递归的终止条件(1)中的情形。
此思路的时间复杂度是O(m * n),其中m为字符串s的长度,n为字符串p的长度,但相比思路一省略了很多重叠子问题的重复计算。空间复杂度是一个boolean类型的m * n的数组,因此空间复杂度是O(m * n)。
public static void main(String[] args) {
System.out.println("请输入表达式1:");
Scanner sc1 = new Scanner(System.in);
String str1 = sc1.nextLine();
String s[] = str1.split("\"");
//String s1 = s[1].substring(1,s[1].length()-1);
System.out.println("请输入表达式2:");
Scanner sc2 = new Scanner(System.in);
String str2 = sc1.nextLine();
String p[] = str2.split("\"");
//String p1 = p[1].substring(0,p[1].length()-1);
System.out.println(isMatch(s[1],p[1]));
}
public static boolean isMatch(String s, String p) {
int ns = s.length() + 1;
int np = p.length() + 1;
boolean[][] matched = new boolean[ns][np];
//当s字符串为空的特殊处理
//f(0, 0)表示s字符串为空,p字符串为空的情形
matched[0][0] = true;
//状态转移过程
for (int i = 0; i < ns; i++) {
for (int j = 1; j < np; j++) {
if(i > 0 && (p.charAt(j - 1) == '.' || p.charAt(j - 1) == s.charAt(i - 1))) {
matched[i][j] = matched[i - 1][j - 1];
}
if(p.charAt(j - 1) == '*') {
if(i == 0 || (s.charAt(i - 1) != p.charAt(j - 2) && p.charAt(j - 2) != '.')) {
matched[i][j] = matched[i][j - 2];
}else {
matched[i][j] = matched[i - 1][j] || matched[i][j - 1] || matched[i][j - 2];
}
}
}
}
return matched[ns - 1][np - 1];
}
代码2
public static boolean isMatch(String s, String p) {
boolean[][] dp = new boolean[s.length()+1][p.length()+1];
dp[0][0] = true;
for (int i = 0; i < p.length(); i++) {
if (p.charAt(i) == '*' && dp[0][i-1]) {
dp[0][i+1] = true;
}
}
for (int i = 0 ; i < s.length(); i++) {
for (int j = 0; j < p.length(); j++) {
if (p.charAt(j) == '.') {
// 该字符匹配成功,使用去掉1个字符的s子串和p子串的匹配结果,作为当前子串的匹配结果
dp[i+1][j+1] = dp[i][j];
}
if (p.charAt(j) == s.charAt(i)) {
// 该字符匹配成功,使用去掉1个字符的s子串和p子串的匹配结果,作为当前子串的匹配结果
dp[i+1][j+1] = dp[i][j];
}
if (p.charAt(j) == '*') {
// 如果遇到 '*'
if (p.charAt(j-1) != s.charAt(i) && p.charAt(j-1) != '.') {
// 该字符和p中上一个字符匹配失败,使用当前s子串和去掉2个字符的p子串的匹配结果,作为当前子串的匹配结果
dp[i+1][j+1] = dp[i+1][j-1];
} else {
// 该字符和p中上一个字符匹配成功,使用下面三个匹配结果作与运算后的结果,作为当前子串的匹配结果
// 1. s子串去掉一个字符,和当前p子串的匹配结果 (in this case, a* counts as multiple a )
// 2. s子串和p子串去掉1个字符的匹配结果(in this case, a* counts as single a)
// 3. s子串和p子串去掉2个字符的匹配结果(in this case, a* counts as empty)
dp[i+1][j+1] = (dp[i+1][j] || dp[i][j+1] || dp[i+1][j-1]);
}
}
}
}
return dp[s.length()][p.length()];
}
## 代码3
```java
```java
在这里插入代码片
```public boolean isMatch(String s, String p) {
int slen = s.length();
int plen = p.length();
boolean dp[][] = new boolean[slen+1][plen+1];
dp[0][0] = true;
for(int j=1;j<=plen;j++){
if(p.charAt(j-1)=='*'){
dp[0][j] = dp[0][j-2];
}
}
for(int i=1;i<=slen;i++){
for(int j=1;j<=plen;j++){
if(s.charAt(i-1)==p.charAt(j-1) || p.charAt(j-1)=='.'){
dp[i][j] = dp[i-1][j-1];
}
else if(p.charAt(j-1)=='*'){
dp[i][j] = dp[i][j-2];
if(s.charAt(i-1)==p.charAt(j-2) || p.charAt(j-2)=='.'){
dp[i][j]= (dp[i-1][j] || dp[i][j-1] || dp[i][j-2]);
}
}
else{
dp[i][j]=false;
}
}
}
return dp[slen][plen];
}
初始化的问题







 京公网安备 11010502036488号
京公网安备 11010502036488号